ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 384
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 < (1,5...2)/Iном, принимают, что при скольжениях, близких к s = 0,1...0,15, изменение х1 и х/2ξ не происходит и kнас = 1. Далее, для каждого из назначенных больших скольжений задаются первоначальными значениями kнас, исходя приближенно из линейного его изменения от kнас = 1 при s = 0,1...0,15 до kнас при s = 1.
Такой метод задания первоначальных значений kнас позволяет правильно учесть влияние насыщения уже после первой или второй итерации.
Расчетные формулы для определения пусковых характеристик с учетом влияния насыщения полями рассеяния сведены в формуляр (табл. 9.33).
Расчет величины CN по (9.265) предлагается выполнить до начала расчета характеристик, так как она остается постоянной при изменении скольжения.
Максимальный момент двигателя вначале определяют по приближенному значению критического скольжения:
SКР ≈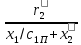
После расчета всей пусковой характеристики значения sкр и Mmax* уточняют.
Таблица 9.33. Формуляр расчета пусковых характеристик асинхронного
двигатели с учетом влияния эффекта вытеснения тока и насыщения от полей рассеяния
Р2 = ... кВт; U1 = ... В; 2р = ...; I1ном = ... A; I'2ном = ... А;
х1 = ... Ом; x'2 = ... Ом; r1 = ... Ом; r'2 = ... Ом;
x12П = ... Ом; sном = ...; CN = ...
Примечания: 1. Полученное в п. 18 значение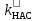
сравнить с принятым kнас (п. 1); при расхождении более 10—15% скорректировать значение kнас и повторить расчет для данного скольжения.
2. Ток I1 (п. 2 и 18) принимается из данных расчета табл. 9.32 (п. 14) для соответствующего скольжения: s = 1 ÷ sкp.
3. Ток I'2ном (п. 20) берется из данных расчета рабочих характеристик двигателя (см. табл. 9.30) для s = sном.
9.14. ОСОБЕННОСТИ РАСЧЕТА ХАРАКТЕРИСТИК АСИНХРОННЫХ
ДВИГАТЕЛЕЙ С РОТОРАМИ, ИМЕЮЩИМИ ДВОЙНУЮ БЕЛИЧЬЮ
КЛЕТКУ ИЛИ ФИГУРНЫЕ ПАЗЫ
Необходимость обеспечения высоких пусковых моментов для нормальной работы ряда приводов привела к довольно широкому распространению асинхронных двигателей с роторами, имеющими двойную беличью клетку со вставными стержнями или фигурными пазами, залитыми алюминием. В последние годы получили распространение также двухклеточные роторы с литыми обмотками. Конфигурация и размеры пазов с литыми обмотками не связаны какими-либо ограничениями, налагаемыми сортаментами профильной меди или латуни, поэтому они могут быть выполнены более рационально с точки зрения использования зубцовой зоны ротора и обеспечения высоких пусковых характеристик по сравнению со сварными клетками.
Расчет магнитной цепи двигателей с фигурными стержнями или двойной клеткой на роторе не отличается от расчета обычных асинхронных машин. Некоторая особенность расчета магнитного напряжения зубцовой зоны ротора учтена в расчетных формулах, приведенных в § 9.9.
Здесь и далее фигурный стержень литой обмотки ротора будем рассматривать как двойную клетку ротора, причем к пусковой клетке отнесем верхнюю (прямоугольную или полуовальную — в зависимости от формы фигурного паза) часть стержня, а к рабочей клетке — его нижнюю часть.
Расчет параметров двухклеточного ротора встречает существенные затруднения, так как распределение токов между стержнями верхней и нижней клеток определяется как соотношением их активных сопротивлений, так и частотой тока в роторе. В то же время при больших скольжениях распределение плотности токов в пределах сечений каждого из стержней также неравномерно из-за действия эффекта вытеснения тока.
При расчете параметров двухклеточных роторов применяют приближенные методы, позволяющие получить общее выражение для активного и индуктивного сопротивлений обеих обмоток ротора r2 и х2 с учетом распределения токов между стержнями верхней и нижней клеток в зависимости от скольжения ротора. Это дает возможность проводить расчет рабочих и пусковых характеристик двигателей по формулам, применяемым для расчета характеристик машин с одноклеточными роторами.
Рассмотрим один из таких приближенных практических методов расчета параметров двухклеточного ротора.
Схема замещения фазы двухклеточного ротора представлена на рис. 9.63. Как видно, сопротивления рабочей и пусковой клеток включены параллельно. Ветвь а—б—в содержит
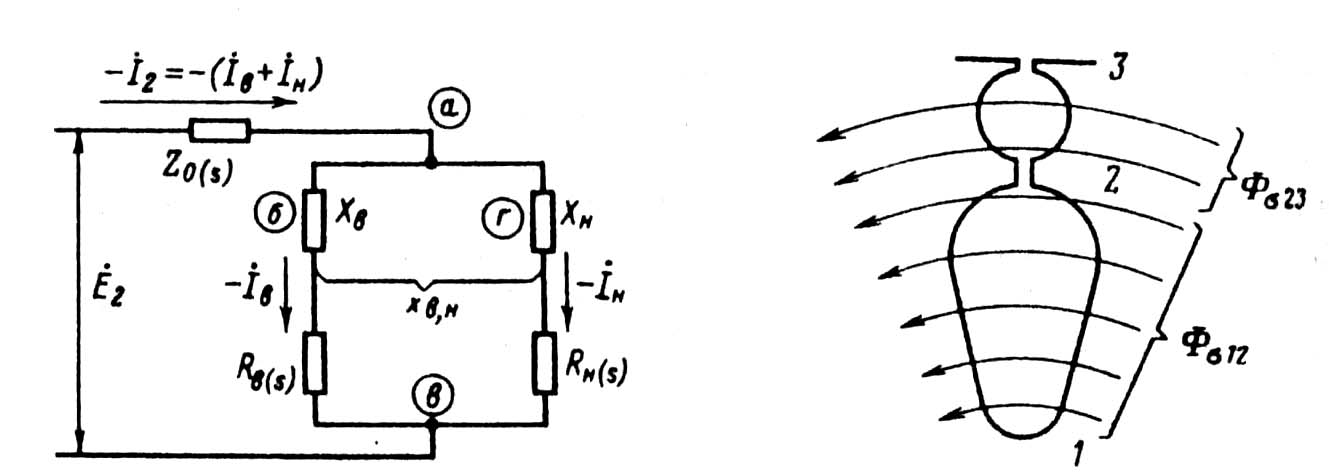
Рис. 9.63. Схема замещения фазы корот- Рис. 9.64. Поток рассеяния в пазу двух-козамкнутого ротора асинхронного дви- клеточного ротора
гателя с двойной беличьей клеткой
сопротивление верхней (пусковой) клетки, ветвь а—г—в сопротивления нижней (рабочей) клетки [6].
Схеме замещения соответствует система уравнений
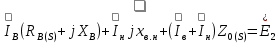(9.287)
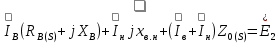
В этих уравнениях и на схеме замещения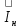
, 
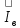— токи в стержнях верхней и нижней клеток; Rв(s) и Rн(s) — активные, а Хв и Хн - индуктивные сопротивления соответственно верхней и нижней клеток; хн.в = хв.н — сопротивление взаимной индукции между стержнями верхней и нижней клеток; Z0(S) — общее для обеих параллельных ветвей сопротивление.
Анализируя картину поля потока рассеяния в пазу двухклеточного ротора (рис. 9.64), видим, что часть потока пазового рассеяния Фσ12 сцеплена только со стержнем нижней клетки (участок паза 1-2), Оставшаяся часть потока Ф σ23, магнитные линии которого проходят через паз выше нижнего стержня (участок паза 2-3), сцеплена со стержнями и верхней, и нижней клеток. Поэтому индуктивное сопротивление стержня нижней клетки определяется проводимостью всего потока рассеяния паза, а сопротивление индуктивности верхнего стержня и взаимная индуктивность верхнего и нижнего стержней определяются проводимостью потока Ф
σ23, так как только эта часть потока сцеплена одновременно и с верхним, и с нижним стержнями.
Исходя из этого, примем следующие обозначения: хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки, определяемое проводимостью верхней часта паза λп.в с учетом потокосцепления с верхним стержнем (поток Ф σ23 создается МДС и верхнего, и нижнего стержней); (хн + хв) — индуктивное сопротивление пазового рассеяния стержня нижней клетки, причем хн определяется проводимостью потоку рассеяния Фσ12 нижней части паза с учетом изменяющегося по высоте паза потокосцепления с нижним стержнем, а хв — проводимостью потоку рассеяния Фσ23 верхней части паза. Потокосцепление потока Фσ23 с нижним стержнем постоянно.
Кроме того, учтем, что сопротивление взаимной индукции хв.н = xн.в определяется также проводимостью верхней части паза потоку Фσ23..
Детальный анализ потоков рассеяния и математическое выражение коэффициентов магнитной проводимости, определяющих указанные выше сопротивления, показывают, что для принятых в электромашиностроении конфигураций и размерных соотношений пазов верхней и нижней клеток без большой погрешности в уравнениях (9.287) можно принять Xв ≈ хн.в ≈ хв.н, так как эти сопротивления обусловлены проводимостью верхней части паза и
Хн = хв + хн.
При принятом допущении система уравнений (9.287) может быть записана следующим образом:
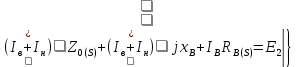(9.288)
Системе уравнений (9.288) соответствует схема замещения, приведенная на рис. (9.288), которая может служить исходной для определения параметров двухклеточного ротора. Практические формулы дня расчета r2 и х2 роторов с общими и раздельными замыкающими кольцами несколько различаются.
Рассмотрим вначале метод расчета r2 и x2 роторов с общими замыкающими кольцами. Для таких роторов коэффициенты при неизвестных токах в уравнениях (9.288) обозначают следующие сопротивления: RB(s) + rB / s — активное сопротивление стержня верхней клетки; RН(s) = rН / s — активное сопротивление стержня нижней клетки; xв = хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки; хн = хп.н — индуктивное сопротивление пазового рассеяния стержня нижней клетки;
Z0(S) = Zкл(s) + jxд
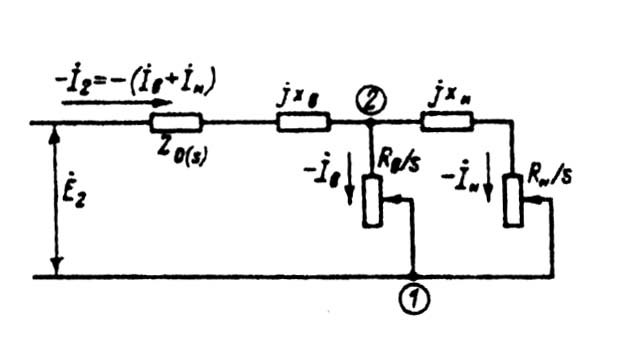
Рис. 9.65. Преобразованная схема замещения фазы
короткозамкнутого ротора с двойной беличьей клеткой
где Zкл(S) — сопротивление участков замыкающих колец между двумя соседними пазами, приведенное к току ротора (см. § 9.10); хд — индуктивное сопротивление дифференциального рассеяния обмотки ротора.
Эквивалентное сопротивление разветвленной цепи этой схемы между токами 1— 2
Zэ(s) =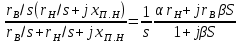
(9.289)
где
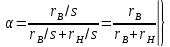(9.290)
Представим Zэ(s) в виде суммы активного rэ и индуктивного хэ сопротивлений:
Zэ(s) =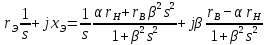
и упростим выражение для rэ и хэ
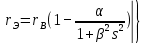(9.291)
Сопротивления rэ и хэ зависят от скольжения, так как изменение соотношения активных и индуктивных сопротивлений стержней, вызванное изменением частоты тока в роторе, изменяет соотношение токов в стержнях рабочей и пусковой клеток.
Такой метод задания первоначальных значений kнас позволяет правильно учесть влияние насыщения уже после первой или второй итерации.
Расчетные формулы для определения пусковых характеристик с учетом влияния насыщения полями рассеяния сведены в формуляр (табл. 9.33).
Расчет величины CN по (9.265) предлагается выполнить до начала расчета характеристик, так как она остается постоянной при изменении скольжения.
Максимальный момент двигателя вначале определяют по приближенному значению критического скольжения:
SКР ≈
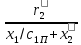
После расчета всей пусковой характеристики значения sкр и Mmax* уточняют.
Таблица 9.33. Формуляр расчета пусковых характеристик асинхронного
двигатели с учетом влияния эффекта вытеснения тока и насыщения от полей рассеяния
Р2 = ... кВт; U1 = ... В; 2р = ...; I1ном = ... A; I'2ном = ... А;
х1 = ... Ом; x'2 = ... Ом; r1 = ... Ом; r'2 = ... Ом;
x12П = ... Ом; sном = ...; CN = ...
| № п/п | Расчетная формула | Едини- цы величины | Скольжение s |
| 1 0,8 ... s = sкр | |||
| 1 |  | — | |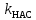
| 2 | 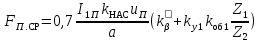 | А | |
| 3 | 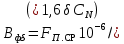 | Тл | |
| 4 |  | — | |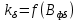
| 5 | 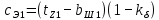 | мм | |
| 6 |  | — | |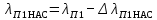
| 7 |  | — | |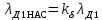
| 8 | 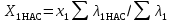 | Ом | |
| 9 |  | — | |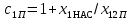
| 10 | 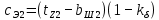 | мм | |
| 11 |  | — | |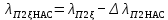
| 12 |  | — | |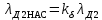
| 13 | 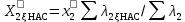 | Ом | |
| 14 | 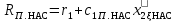 | Ом | |
| 15 | 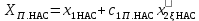 | Ом | |
| 16 | 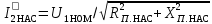 | А | |
| 17 | 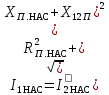 | A | |
| 18 |  | — | |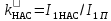
| 19 |  | — | |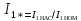
| 20 |  | — | |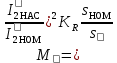
Примечания: 1. Полученное в п. 18 значение
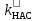сравнить с принятым kнас (п. 1); при расхождении более 10—15% скорректировать значение kнас и повторить расчет для данного скольжения.2. Ток I1 (п. 2 и 18) принимается из данных расчета табл. 9.32 (п. 14) для соответствующего скольжения: s = 1 ÷ sкp.
3. Ток I'2ном (п. 20) берется из данных расчета рабочих характеристик двигателя (см. табл. 9.30) для s = sном.
9.14. ОСОБЕННОСТИ РАСЧЕТА ХАРАКТЕРИСТИК АСИНХРОННЫХ
ДВИГАТЕЛЕЙ С РОТОРАМИ, ИМЕЮЩИМИ ДВОЙНУЮ БЕЛИЧЬЮ
КЛЕТКУ ИЛИ ФИГУРНЫЕ ПАЗЫ
Необходимость обеспечения высоких пусковых моментов для нормальной работы ряда приводов привела к довольно широкому распространению асинхронных двигателей с роторами, имеющими двойную беличью клетку со вставными стержнями или фигурными пазами, залитыми алюминием. В последние годы получили распространение также двухклеточные роторы с литыми обмотками. Конфигурация и размеры пазов с литыми обмотками не связаны какими-либо ограничениями, налагаемыми сортаментами профильной меди или латуни, поэтому они могут быть выполнены более рационально с точки зрения использования зубцовой зоны ротора и обеспечения высоких пусковых характеристик по сравнению со сварными клетками.
Расчет магнитной цепи двигателей с фигурными стержнями или двойной клеткой на роторе не отличается от расчета обычных асинхронных машин. Некоторая особенность расчета магнитного напряжения зубцовой зоны ротора учтена в расчетных формулах, приведенных в § 9.9.
Здесь и далее фигурный стержень литой обмотки ротора будем рассматривать как двойную клетку ротора, причем к пусковой клетке отнесем верхнюю (прямоугольную или полуовальную — в зависимости от формы фигурного паза) часть стержня, а к рабочей клетке — его нижнюю часть.
Расчет параметров двухклеточного ротора встречает существенные затруднения, так как распределение токов между стержнями верхней и нижней клеток определяется как соотношением их активных сопротивлений, так и частотой тока в роторе. В то же время при больших скольжениях распределение плотности токов в пределах сечений каждого из стержней также неравномерно из-за действия эффекта вытеснения тока.
При расчете параметров двухклеточных роторов применяют приближенные методы, позволяющие получить общее выражение для активного и индуктивного сопротивлений обеих обмоток ротора r2 и х2 с учетом распределения токов между стержнями верхней и нижней клеток в зависимости от скольжения ротора. Это дает возможность проводить расчет рабочих и пусковых характеристик двигателей по формулам, применяемым для расчета характеристик машин с одноклеточными роторами.
Рассмотрим один из таких приближенных практических методов расчета параметров двухклеточного ротора.
Схема замещения фазы двухклеточного ротора представлена на рис. 9.63. Как видно, сопротивления рабочей и пусковой клеток включены параллельно. Ветвь а—б—в содержит
Рис. 9.63. Схема замещения фазы корот- Рис. 9.64. Поток рассеяния в пазу двух-козамкнутого ротора асинхронного дви- клеточного ротора
гателя с двойной беличьей клеткой
сопротивление верхней (пусковой) клетки, ветвь а—г—в сопротивления нижней (рабочей) клетки [6].
Схеме замещения соответствует система уравнений
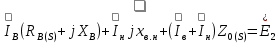(9.287)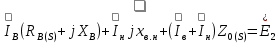 В этих уравнениях и на схеме замещения
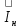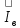, — токи в стержнях верхней и нижней клеток; Rв(s) и Rн(s) — активные, а Хв и Хн - индуктивные сопротивления соответственно верхней и нижней клеток; хн.в = хв.н — сопротивление взаимной индукции между стержнями верхней и нижней клеток; Z0(S) — общее для обеих параллельных ветвей сопротивление.Анализируя картину поля потока рассеяния в пазу двухклеточного ротора (рис. 9.64), видим, что часть потока пазового рассеяния Фσ12 сцеплена только со стержнем нижней клетки (участок паза 1-2), Оставшаяся часть потока Ф σ23, магнитные линии которого проходят через паз выше нижнего стержня (участок паза 2-3), сцеплена со стержнями и верхней, и нижней клеток. Поэтому индуктивное сопротивление стержня нижней клетки определяется проводимостью всего потока рассеяния паза, а сопротивление индуктивности верхнего стержня и взаимная индуктивность верхнего и нижнего стержней определяются проводимостью потока Ф
σ23, так как только эта часть потока сцеплена одновременно и с верхним, и с нижним стержнями.
Исходя из этого, примем следующие обозначения: хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки, определяемое проводимостью верхней часта паза λп.в с учетом потокосцепления с верхним стержнем (поток Ф σ23 создается МДС и верхнего, и нижнего стержней); (хн + хв) — индуктивное сопротивление пазового рассеяния стержня нижней клетки, причем хн определяется проводимостью потоку рассеяния Фσ12 нижней части паза с учетом изменяющегося по высоте паза потокосцепления с нижним стержнем, а хв — проводимостью потоку рассеяния Фσ23 верхней части паза. Потокосцепление потока Фσ23 с нижним стержнем постоянно.
Кроме того, учтем, что сопротивление взаимной индукции хв.н = xн.в определяется также проводимостью верхней части паза потоку Фσ23..
Детальный анализ потоков рассеяния и математическое выражение коэффициентов магнитной проводимости, определяющих указанные выше сопротивления, показывают, что для принятых в электромашиностроении конфигураций и размерных соотношений пазов верхней и нижней клеток без большой погрешности в уравнениях (9.287) можно принять Xв ≈ хн.в ≈ хв.н, так как эти сопротивления обусловлены проводимостью верхней части паза и
Хн = хв + хн.
При принятом допущении система уравнений (9.287) может быть записана следующим образом:
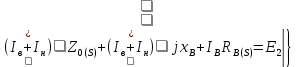(9.288)Системе уравнений (9.288) соответствует схема замещения, приведенная на рис. (9.288), которая может служить исходной для определения параметров двухклеточного ротора. Практические формулы дня расчета r2 и х2 роторов с общими и раздельными замыкающими кольцами несколько различаются.
Рассмотрим вначале метод расчета r2 и x2 роторов с общими замыкающими кольцами. Для таких роторов коэффициенты при неизвестных токах в уравнениях (9.288) обозначают следующие сопротивления: RB(s) + rB / s — активное сопротивление стержня верхней клетки; RН(s) = rН / s — активное сопротивление стержня нижней клетки; xв = хп.в — индуктивное сопротивление пазового рассеяния стержня верхней клетки; хн = хп.н — индуктивное сопротивление пазового рассеяния стержня нижней клетки;
Z0(S) = Zкл(s) + jxд
Рис. 9.65. Преобразованная схема замещения фазы
короткозамкнутого ротора с двойной беличьей клеткой
где Zкл(S) — сопротивление участков замыкающих колец между двумя соседними пазами, приведенное к току ротора (см. § 9.10); хд — индуктивное сопротивление дифференциального рассеяния обмотки ротора.
Эквивалентное сопротивление разветвленной цепи этой схемы между токами 1— 2
Zэ(s) =
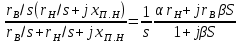(9.289)где
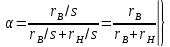(9.290)Представим Zэ(s) в виде суммы активного rэ и индуктивного хэ сопротивлений:
Zэ(s) =
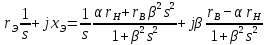
и упростим выражение для rэ и хэ
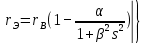(9.291)Сопротивления rэ и хэ зависят от скольжения, так как изменение соотношения активных и индуктивных сопротивлений стержней, вызванное изменением частоты тока в роторе, изменяет соотношение токов в стержнях рабочей и пусковой клеток.