Файл: Отчет о прохождении учебной ознакомительной практики по математике.docx
Добавлен: 09.11.2023
Просмотров: 186
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ: 10.
Задание №3
Т
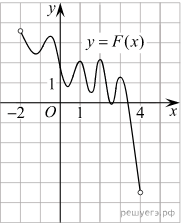
ип 7 № 323171На рисунке изображён график функции y=F (x) — одной из первообразных некоторой функции f (x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке [-1;3].
Решение:
П
о определению первообразной на интервале (−2; 4) справедливо равенствоf(x)=F’(x)
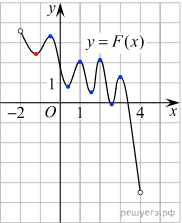
Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,2; −0,4; 0,4; 1; 1,6; 2; 2,6; 3. Из них на отрезке [−1; 3] лежат 7 точек (выделены синим). Таким образом, на отрезке [−1; 3] уравнение f(x)= 0 имеет 7 решений.
Ответ: 7.
Задание №4
Тип 7 № 323173
Н
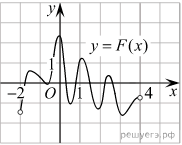а рисунке изображён график функции y=F(x) - одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]. Решение:
По определению первообразной на интервале (−2; 4) справедливо равенство
f
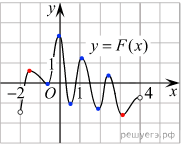
(x)=F’(x) Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,6; −0,6; −0,1; 0,5; 1,2; 1,8; 2,4; 3,2. Из них на отрезке [−1; 3] лежат 6 точек. Таким образом, на отрезке [−1; 3] уравнение f(x) = 0 имеет 6 решений.
Ответ: 6.
Задание №5
Тип 7 № 323175
Н
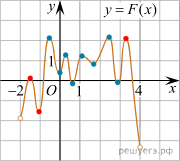
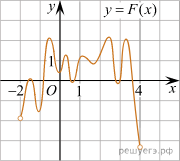а рисунке изображён график функции y=F(x), которая является одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3] Решение:
По определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
Cследовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Из них на отрезке [−1; 3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x) = 0 имеет 8 решений.
Ответ: 8.
З
адание №6Тип 7 № 323177
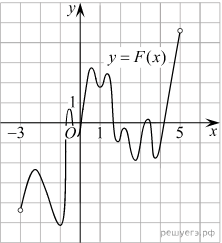
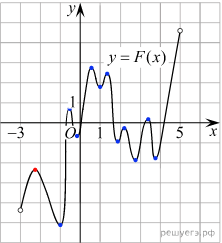
На рисунке изображён график функции y=F(x), которая является одной из первообразных некоторой функции f(x), определённой на интервале (-3;5) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4]
Решение:
По определению первообразной на интервале (−3; 5) справедливо равенство
f
(x)=F’(x)Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,4; −0,8; −0,6; −0,2; 0,6; 1; 1,2; 1,8; 2,2; 2,8; 3,2; 3,8. Из них на отрезке [−2; 4] лежат 11 точек. Таким образом, на отрезке [−2; 4] уравнение f(x) = 0 имеет 11 решений.
Ответ: 11.
Задание №7
Т
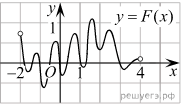
ип 7 №323179На рисунке изображён график функции y=F(x), которая является одной из первообразных некоторой функции f(x), определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
По определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
С
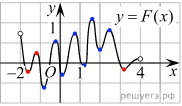ледовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции
F(x). Это точки −1,8; −1,2; −0,8; −0,4; 0,2; 0,8; 1,2; 1,6; 2; 2,4; 3,2; 3,8. Из них на отрезке [-1;3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)=0 имеет 8 решений.
Ответ: 8.
Задание №8
Тип 7 № 509572
Н
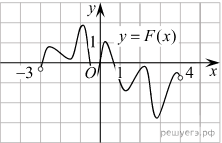а рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 4). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 3].Решение:
По определению первообразной на интервале (−3; 4) справедливо равенство
f(x)=F’(x)
С
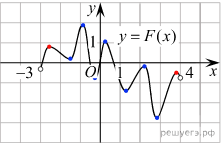ледовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x). Из них на отрезке [−2;3] лежат 7 точек. Таким образом, на отрезке [−2;3] уравнение f(x)=0 имеет 7 решений.Ответ: 7.
Задание №9
Т
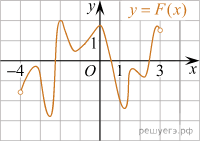ип 7 №509919На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−4; 3). Найдите количество решений уравнения f(x) = 0 на отрезке [−3; 1].
Решение:
По определению первообразной на интервале (−4; 3) справедливо равенство
f(x)=F’(x)
С
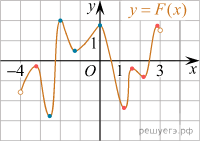ледовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x). Из них на отрезке [−3;1] лежат 4 точки (выделены голубым).Таким образом, на отрезке [−3;1] уравнение f(x) = 0 на отрезке имеет 4 решения.
Ответ: 4.
Задание №10
Тип 7 №523988
Н
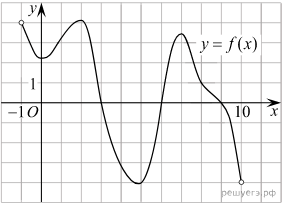а рисунке изображён график дифференцируемой функции y=f(x) определённой на интервале (−1; 10). Найдите количество решений уравнения f’(x)=0 на отрезке [4; 8]. Решение:
Р
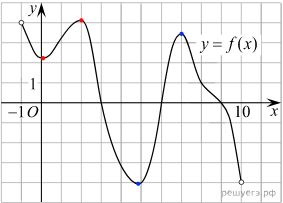ешениями уравнения
f’(x)=0 являются точки экстремумов изображенной на рисунке функции f(x) Из них на отрезке [4; 8] лежат 2 точки. Таким образом, на отрезке [4; 8] уравнение f(x) = 0 имеет 2 решения.
Ответ: 2.
Задание №11
Тип 7 №524015
Н
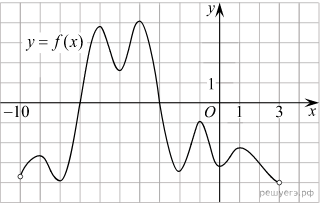а рисунке изображён график дифференцируемой функции y=f(x) определённой на интервале (−10; 3). Найдите количество решений уравнения f’(x)=0 на отрезке [−7,5; −2,5].Р
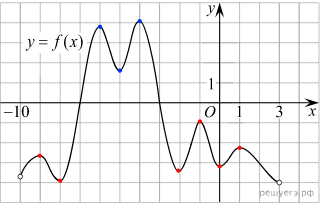ешение:Решениями уравнения f’(x)=0 являются точки экстремумов изображенной на рисунке функции f(x) Из них на отрезке (−10; 3) лежат 9 точек. Таким образом, на отрезке [−7,5; −2,5] уравнение f’(x)=0 имеет 3 решения.
Ответ: 3.
Задание №12
Тип 7 №548505
Н
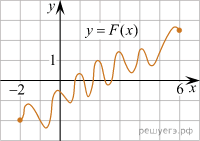а рисунке изображён график функции y = F(x) и одной из первообразных некоторой функции f(x) определённой на интервале (-2:6) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;5]Р
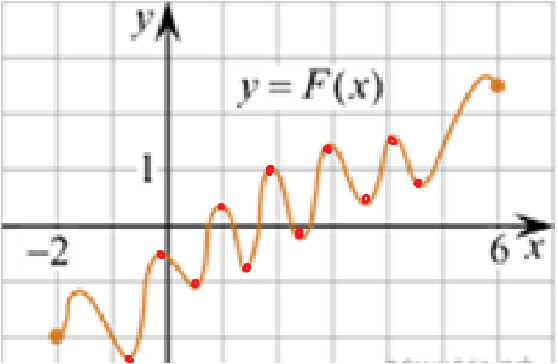ешение:По определению первообразной на интервале (−2; 6) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов (минимумы, максимумы). У изображенной на рисунке функции F(x) на отрезке [−1; 5] лежат 11 точек. Таким образом, на отрезке [−1; 5] уравнение f(x)=0 имеет 11 решений.
Ответ: 11.
Задание №13
Тип 7 №559595
Н
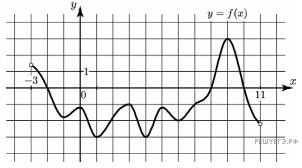а рисунке изображён график функции y=f (x), определённой на интервале (−3; 11). Найдите наименьшее значение функции f(x)на отрезке [2; 9,5].Решение:
Из графика находим, что наименьшее значение функции f