Файл: Отчет о прохождении учебной ознакомительной практики по математике.docx
Добавлен: 09.11.2023
Просмотров: 190
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
F(6)-F(2) где F(x) — одна из первообразных функции f(x)
Р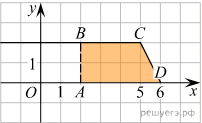
ешение:
Разность значений первообразной в точках 6 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому
F(b)-F(a)=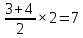
Ответ: 7
Задание №25
Т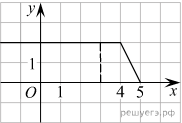
ип 7 №323185
На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(5)-F(3) где F(x) — одна из первообразных функции f(x)
Р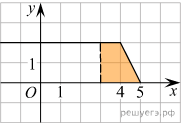
ешение:
Разность значений первообразной в точках 5 и 3 равна площади выделенной на рисунке трапеции. Поэтому
F(b)-F(a)=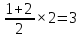
Ответ: 3
Задание №26
Т
ип 7 №323275
На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(6) где F(x) — одна из первообразных функции f(x)
Р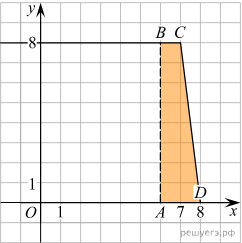
ешение:
Разность значений первообразной в точках 8 и 6 равна площади выделенной на рисунке трапеции ABCD. Поэтому
F(b)-F(a)=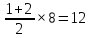
Ответ: 12
Задание №27
Т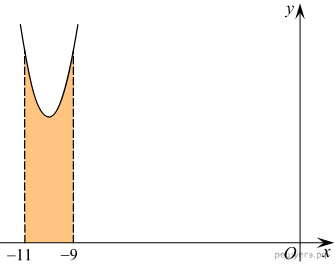
ип 7 №323283
На рисунке изображён график функции y = f(x). Функция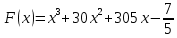
— одна из первообразных функции
f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках -9 и -11.
Имеем:
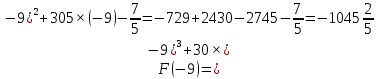
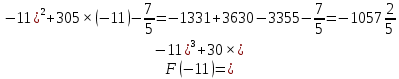
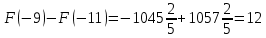
Ответ: 12
Задание №28
Т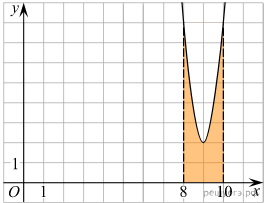
ип 7 №323373
На рисунке изображён график функции y = f(x). Функция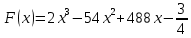
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 10 и 8.
Имеем
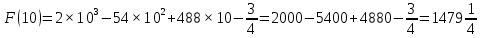
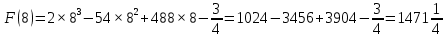
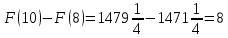
Ответ: 8
Задание №29
Тип 7 №323375
Н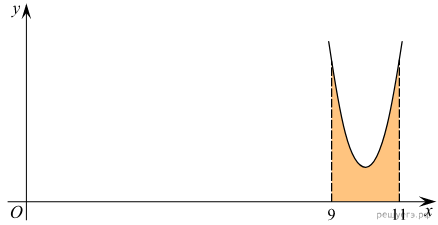
а рисунке изображён график функции y = f(x). Функция 
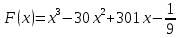— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 9 и 11.
Имеем
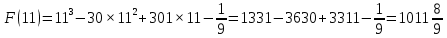
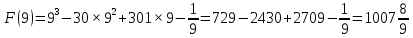
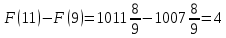
Ответ: 4
Задание №30
Т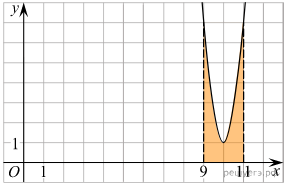
ип 7 №323
На рисунке изображён график функции y =
f(x). Функция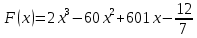
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 9 и 11.
Имеем
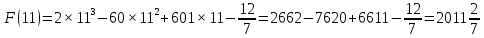
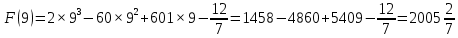
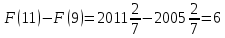
Ответ: 6
Задание №31
Тип 7 №323383
Н
а рисунке изображён график некоторой функции y = f(x). Функция F(x) =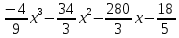
одна из первообразных функций f(x). Найдите площадь закрашенной фигуры.
Решение:
Найдем формулу, задающую функцию f(x)график которой изображён на рисунке.
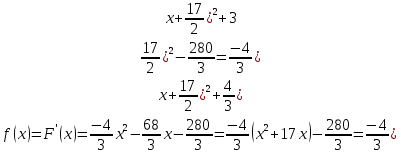
Следовательно, график функции f(x) получен сдвигом графика функции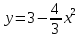
на 8.5 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции 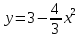и отрезком [-1.5;1.5] оси абсцисс. Имеем
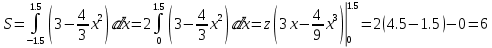
Ответ: 6
Задание №32
Т
ип 7 №323477
На рисунке изображён график некоторой функции y = f(x). Функция F(x) =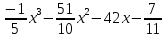
одна из первообразных функций f(x). Найдите площадь закрашенной фигуры.
Решение:
Функция непрерывна и положительна на отрезке от 7 до 10, поэтому площадь закрашенной фигуры в данном случаем можно вычислить по формуле: S=F(b)-F(a) где b и a — это соответственно координаты правого и левого концов отрезка. Вычислим:
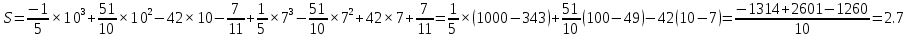
Ответ: 2.7
З
адание №33
Тип 7 №500890
На рисунке изображен график некоторой функции y = f(x). Пользуясь рисунком, вычислите определенный интеграл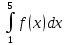
Решение:
Определенный интеграл от функции f(x) по отрезку [1;5] дает значение площади под графика функции f(x) на отрезке. Область под графиком разбивается на прямоугольный треугольник, площадь которого Sтр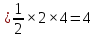
и прямоугольник, площадь которого Sпр=
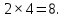Сумма этих площадей дает искомый интеграл
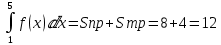
Ответ: 12
_________ _______________ ________________________
(дата) (подпись) (расшифровка подписи)
Р
ешение:Разность значений первообразной в точках 6 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому
F(b)-F(a)=
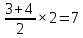
Ответ: 7
Задание №25
Т
ип 7 №323185На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(5)-F(3) где F(x) — одна из первообразных функции f(x)
Р
ешение:Разность значений первообразной в точках 5 и 3 равна площади выделенной на рисунке трапеции. Поэтому
F(b)-F(a)=
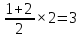
Ответ: 3
Задание №26
Т
ип 7 №323275На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(6) где F(x) — одна из первообразных функции f(x)
Р
ешение:Разность значений первообразной в точках 8 и 6 равна площади выделенной на рисунке трапеции ABCD. Поэтому
F(b)-F(a)=
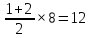
Ответ: 12
Задание №27
Т
ип 7 №323283На рисунке изображён график функции y = f(x). Функция
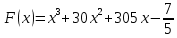— одна из первообразных функции
f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках -9 и -11.
Имеем:
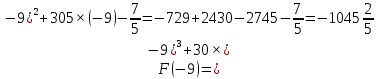
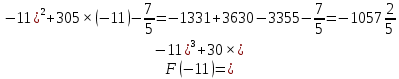
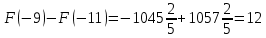
Ответ: 12
Задание №28
Т
ип 7 №323373На рисунке изображён график функции y = f(x). Функция
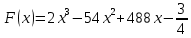— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 10 и 8.
Имеем
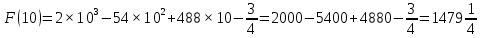
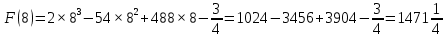
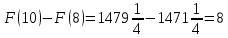
Ответ: 8
Задание №29
Тип 7 №323375
Н
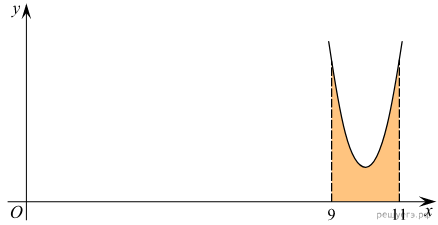а рисунке изображён график функции y = f(x). Функция 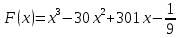— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 9 и 11.
Имеем
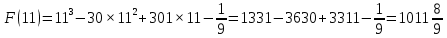
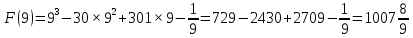
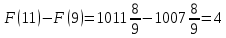
Ответ: 4
Задание №30
Т
ип 7 №323На рисунке изображён график функции y =
f(x). Функция
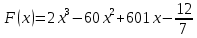— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках 9 и 11.
Имеем
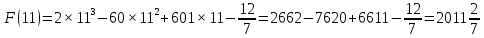
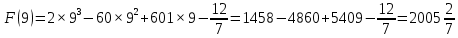
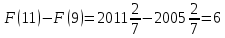
Ответ: 6
Задание №31
Тип 7 №323383
Н
а рисунке изображён график некоторой функции y = f(x). Функция F(x) =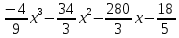 одна из первообразных функций f(x). Найдите площадь закрашенной фигуры.Решение:
Найдем формулу, задающую функцию f(x)график которой изображён на рисунке.
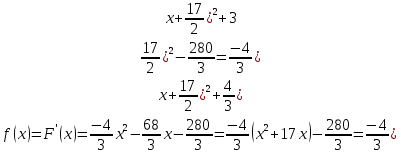
Следовательно, график функции f(x) получен сдвигом графика функции
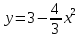на 8.5 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции 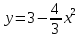и отрезком [-1.5;1.5] оси абсцисс. Имеем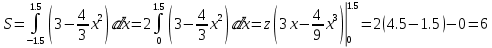 Ответ: 6
Задание №32
Т
ип 7 №323477На рисунке изображён график некоторой функции y = f(x). Функция F(x) =
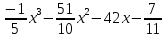одна из первообразных функций f(x). Найдите площадь закрашенной фигуры.Решение:
Функция непрерывна и положительна на отрезке от 7 до 10, поэтому площадь закрашенной фигуры в данном случаем можно вычислить по формуле: S=F(b)-F(a) где b и a — это соответственно координаты правого и левого концов отрезка. Вычислим:
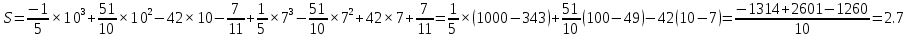
Ответ: 2.7
З
адание №33Тип 7 №500890
На рисунке изображен график некоторой функции y = f(x). Пользуясь рисунком, вычислите определенный интеграл
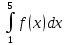
Решение:
Определенный интеграл от функции f(x) по отрезку [1;5] дает значение площади под графика функции f(x) на отрезке. Область под графиком разбивается на прямоугольный треугольник, площадь которого Sтр
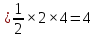и прямоугольник, площадь которого Sпр= 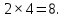Сумма этих площадей дает искомый интеграл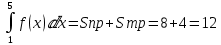 Ответ: 12
_________ _______________ ________________________
(дата) (подпись) (расшифровка подписи)