Файл: Отчет о прохождении учебной ознакомительной практики по математике.docx
Добавлен: 09.11.2023
Просмотров: 185
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(x) на отрезке [2; 9,5] равно −3: самая нижняя ордината графика на данном отрезке y(4)=-3
Ответ: −3.
Задание №14
Тип 7 №323077
Н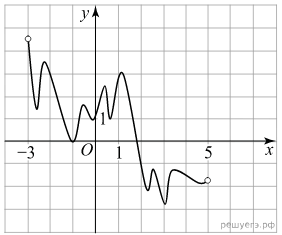 а рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
а рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Решение:
П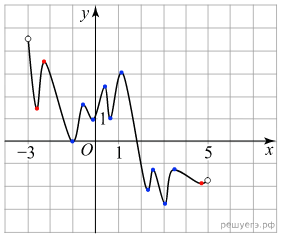 о определению первообразной на интервале (−3; 5) справедливо равенство
о определению первообразной на интервале (−3; 5) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) На рисунке точки, в которых f(x)=0 выделены красным и синим цветом. Из них на отрезке [−2;4] лежат 10 точек (синие точки). Таким образом, на отрезке [−2;4] уравнение f(x)=0 имеет 10 решений
Ответ: 10.
Задание №15
Т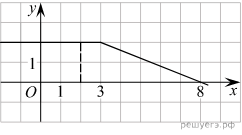 ип 7 №323078
ип 7 №323078
На рисунке изображён график некоторой функции y=f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)− F(2), где F(x) — одна из первообразных функции f(x).
Решение:
Р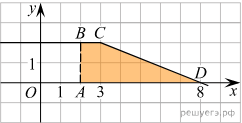 азность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции АВСD. Поэтому
азность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции АВСD. Поэтому
F(b)-F(a)=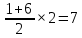
Ответ: 7.
Задание №16
Т
ип 7 №323079
На рисунке изображён график функции y = f(x). Функция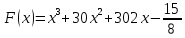 — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках -9 и -11
Имеем:
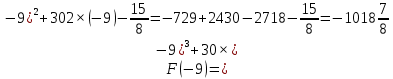
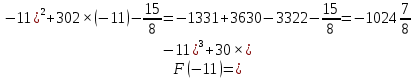
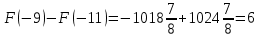
Ответ:6
Задание №16
Т ип 7 №323080
ип 7 №323080
На рисунке изображён график некоторой функции y = f(x). Функция одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решение:
Найдем формулу, задающую функцию y = f(x) рафик которой изображён на рисунке
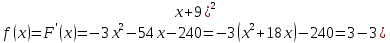
Следовательно, график функции f(x) получен сдвигом графика функции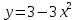 на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции
на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции 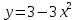 и отрезком [-1;1] оси абсцисс. Имеем:
и отрезком [-1;1] оси абсцисс. Имеем:
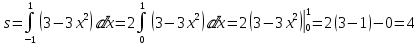
Ответ: 4
Задание №17
Т ип 7 №323081
ип 7 №323081
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;6) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;5]
Решение:
По определению первообразной на интервале (−2; 6) справедливо равенство
f
(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов (минимумы, максимумы). У изображенной на рисунке функции F(x) на отрезке [−1; 5] лежат 10 точек. Таким образом, на отрезке [−1; 5] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Задание №18
Т ип 7 №323083
ип 7 №323083
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-3;6) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;5]
Решение:
П о определению первообразной на интервале (−3; 6) справедливо равенство
о определению первообразной на интервале (−3; 6) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов (максимумы, минимумы). У изображенной на рисунке функции F(x) на отрезке [−2; 5] лежат 10 точек (на рисунке выделены синим цветом). Таким образом, на отрезке [−2; 5] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Задание №19
Т ип 7 №323171
ип 7 №323171
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,2; −0,4; 0,4; 1; 1,6; 2; 2,6; 3. Из них на отрезке [−1; 3] лежат 7 точек (выделены синим). Таким образом, на отрезке [−1; 3] уравнение
f(x)= 0 имеет 7 решений.
Ответ: 7
Задание №20
Т ип 7 №323173
ип 7 №323173
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)= 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,6; −0,6; −0,1; 0,5; 1,2; 1,8; 2,4; 3,2. Из них на отрезке [−1; 3] лежат 6 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)= 0 имеет 6 решений.
Ответ: 6.
Задание №21
Тип 7 №323175
Н а рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
а рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)= 0 являются точки экстремумов изображенной на рисунке функции F(x) Из них на отрезке [−1; 3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)= 0 имеет 8 решений.
Ответ: 8.
Задание №22
Т ип 7 №323177
ип 7 №323177
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-3;5) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4]
Решение:
По определению первообразной на интервале (−3; 5) справедливо равенство
f (x)=F’(x)
(x)=F’(x)
Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,4; −0,8; −0,6; −0,2; 0,6; 1; 1,2; 1,8; 2,2; 2,8; 3,2; 3,8. Из них на отрезке [−2; 4] лежат 11 точек. Таким образом, на отрезке [−2; 4] уравнение f(x)=0 имеет 11 решений.
Ответ: 11.
Задание №23
Т ип 7 №323179
ип 7 №323179
На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенство
f(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x). Это точки −1,8; −1,2; −0,8; −0,4; 0,2; 0,8; 1,2; 1,6; 2; 2,4; 3,2; 3,8. Из них на отрезке [−1; 3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)=0 имеет 8 решений.
Ответ: 8.
Задание №24
Т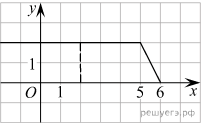 ип 7 №323183
ип 7 №323183
На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
Ответ: −3.
Задание №14
Тип 7 №323077
Н
 а рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
а рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].Решение:
П
 о определению первообразной на интервале (−3; 5) справедливо равенство
о определению первообразной на интервале (−3; 5) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) На рисунке точки, в которых f(x)=0 выделены красным и синим цветом. Из них на отрезке [−2;4] лежат 10 точек (синие точки). Таким образом, на отрезке [−2;4] уравнение f(x)=0 имеет 10 решений
Ответ: 10.
Задание №15
Т
 ип 7 №323078
ип 7 №323078На рисунке изображён график некоторой функции y=f (x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)− F(2), где F(x) — одна из первообразных функции f(x).
Решение:
Р
 азность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции АВСD. Поэтому
азность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции АВСD. ПоэтомуF(b)-F(a)=
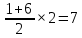
Ответ: 7.
Задание №16
Т

ип 7 №323079
На рисунке изображён график функции y = f(x). Функция
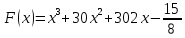 — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.Решение:
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках -9 и -11
Имеем:
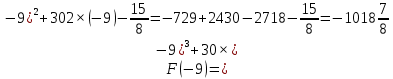
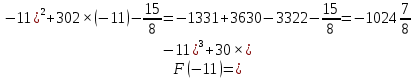
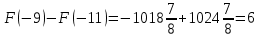
Ответ:6
Задание №16
Т
 ип 7 №323080
ип 7 №323080На рисунке изображён график некоторой функции y = f(x). Функция
 одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.Решение:
Найдем формулу, задающую функцию y = f(x) рафик которой изображён на рисунке
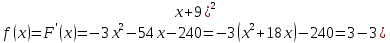
Следовательно, график функции f(x) получен сдвигом графика функции
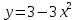 на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции
на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции 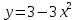 и отрезком [-1;1] оси абсцисс. Имеем:
и отрезком [-1;1] оси абсцисс. Имеем: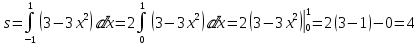
Ответ: 4
Задание №17
Т
 ип 7 №323081
ип 7 №323081На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;6) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;5]
Решение:
По определению первообразной на интервале (−2; 6) справедливо равенство
f

(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов (минимумы, максимумы). У изображенной на рисунке функции F(x) на отрезке [−1; 5] лежат 10 точек. Таким образом, на отрезке [−1; 5] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Задание №18
Т
 ип 7 №323083
ип 7 №323083На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-3;6) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;5]
Решение:
П
 о определению первообразной на интервале (−3; 6) справедливо равенство
о определению первообразной на интервале (−3; 6) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов (максимумы, минимумы). У изображенной на рисунке функции F(x) на отрезке [−2; 5] лежат 10 точек (на рисунке выделены синим цветом). Таким образом, на отрезке [−2; 5] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Задание №19
Т
 ип 7 №323171
ип 7 №323171На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П
 о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,2; −0,4; 0,4; 1; 1,6; 2; 2,6; 3. Из них на отрезке [−1; 3] лежат 7 точек (выделены синим). Таким образом, на отрезке [−1; 3] уравнение
f(x)= 0 имеет 7 решений.
Ответ: 7
Задание №20
Т
 ип 7 №323173
ип 7 №323173На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П
 о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x)= 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −1,6; −0,6; −0,1; 0,5; 1,2; 1,8; 2,4; 3,2. Из них на отрезке [−1; 3] лежат 6 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)= 0 имеет 6 решений.
Ответ: 6.
Задание №21
Тип 7 №323175
Н
 а рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
а рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3] Решение:
П
 о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x)= 0 являются точки экстремумов изображенной на рисунке функции F(x) Из них на отрезке [−1; 3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)= 0 имеет 8 решений.
Ответ: 8.
Задание №22
Т
 ип 7 №323177
ип 7 №323177На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-3;5) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4]
Решение:
По определению первообразной на интервале (−3; 5) справедливо равенство
f
 (x)=F’(x)
(x)=F’(x)Следовательно, решениями уравнения f(x) = 0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,4; −0,8; −0,6; −0,2; 0,6; 1; 1,2; 1,8; 2,2; 2,8; 3,2; 3,8. Из них на отрезке [−2; 4] лежат 11 точек. Таким образом, на отрезке [−2; 4] уравнение f(x)=0 имеет 11 решений.
Ответ: 11.
Задание №23
Т
 ип 7 №323179
ип 7 №323179На рисунке изображён график функции y = F(x) одной из первообразных некоторой функции f(x) определённой на интервале (-2;4) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-1;3]
Решение:
П
 о определению первообразной на интервале (−2; 4) справедливо равенство
о определению первообразной на интервале (−2; 4) справедливо равенствоf(x)=F’(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x). Это точки −1,8; −1,2; −0,8; −0,4; 0,2; 0,8; 1,2; 1,6; 2; 2,4; 3,2; 3,8. Из них на отрезке [−1; 3] лежат 8 точек. Таким образом, на отрезке [−1; 3] уравнение f(x)=0 имеет 8 решений.
Ответ: 8.
Задание №24
Т
 ип 7 №323183
ип 7 №323183На рисунке изображён график некоторой функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите