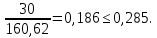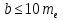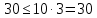Файл: Кафедра курсовой проект проектирование привода рабочей машины тема проекта Руководитель Калиновская Т. Г. подпись, дата фио.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 168
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=Р2
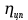= 3,17 0,95 = 3,0 кВт;
:
= 
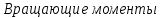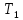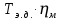= 9550 
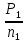= 9550 
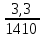= 22,4 Нм.
= 
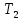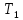
= 22,4 5 0,96 = 107,4 Нм.
= ∙ 
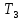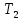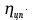
= 107,4 2,35 095 = 239,8 Нм.
Таблица 1 -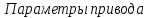
2 Выбор материалов зубчатой передачи. Определение допускаемых контактных и изгибных напряжений
2.1 Выбор материалов для зубчатых колес
Шестерня – сталь 45; Dзаг более 120 мм; термообработка – улучшение; НВср1=215. [2, табл.7].
Колесо – сталь 45, Dзаг любой; термообработка – нормализация; НВср2=190. [2, табл.7].
2.2 Определение допустимых контактных напряжений
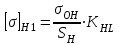
где σон – предел контактной выносливости, МПа, σон=2НВср+70. [2, табл.7].
Sн – коэффициент безопасности, Sн=1,1. [2, табл.7].
Кнл =1,0 – коэффициент долговечности.
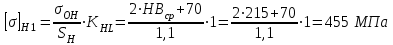
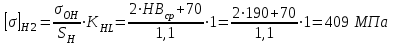
2.3. Определение допускаемых изгибных напряжений
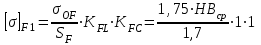
где σof – предел изгибной выносливости, МПа, σof= 1,75∙НВср. [2, табл.8].
Sf – коэффициент безопасности, Sf=1,7. [2, табл.8].
КFL =1,0 – коэффициент долговечности;
КFC – коэффициент учитывающий влияние двухстороннего;
приложения нагрузки, КFС =1,0. [2, табл.8].
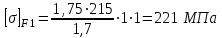
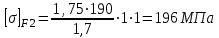
3 Расчет закрытой конической передачи с прямыми зубьями
3.1 Проектный расчет
Из условия контактной прочности находим ориентировочное значение среднего делительного диаметра шестерни:
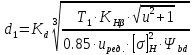, мм.
где Т1 – крутящий момент на валу шестерни, Нм;
КНβ – коэффициент неравномерности распределения нагрузки по длине
зуба, зависящий от твердости зубьев передачи и расположения
колес относительно опор, КНβ = 1,1. [2, табл.10].
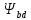– коэффициент ширины венца колеса по среднему делительному
диаметру шестерни,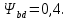
[2, табл.11].
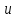– передаточное отношение проектируемой конической передачи;
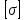Н – допускаемые контактные напряжения для материала колеса, как
наиболее слабого звена передачи, МПа;
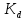– вспомогательный коэффициент, для стальных колес с прямым
зубом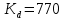
. [2, табл.9].
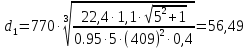мм.
Ширину зубчатого венца колеса определяем по формуле:
b =
·
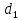, мм
b = 0,4 · 56,49 = 22,6 мм.
Находим внешние делительные диаметры шестерни:
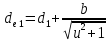, мм.
.
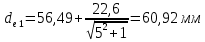Колеса:
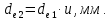
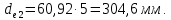
Полученные при расчете величины bи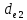
округляем до стандартных значений, b = 45 мм и 
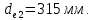Так как значение b, найденное расчетом составляет b=22,6, а по таблице b=45, то принимаем b=30 мм.
Внешний окружной модуль передачи рассчитываем по формуле:
.
.
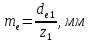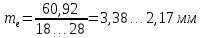Принимае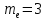м
мм.
Число зубьев колеса определяем по формуле:
z2 =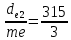
= 105
Принимаем z2=105.
z1 =
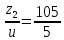= 21
Принимаем z1=21.
Фактическое передаточное отношение:
Uф =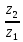
= 105/21 = 5.
Отклонение:
= 
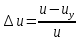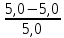∙ 100% = 0 % < 4%.
Углы делительного конуса:
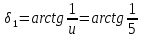=11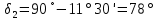°30'
30'
Основные геометрические параметры определяем по формулам:
Внешний делительный диаметр:
.
.
.
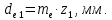
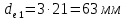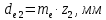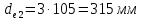Внешний диаметр вершин зубьев:
.
.
.
.
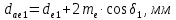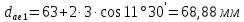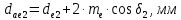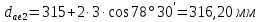Внешнее конусное расстояние:
.
.
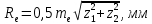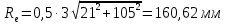Средний модуль:
.
.
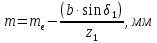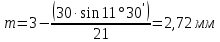Средний делительный диаметр:
.
.
.
.
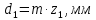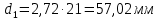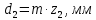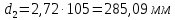Высота головки зуба:
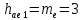мм.
Высота ножки зуба:
=
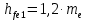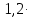3= 3,6 мм.
Угол ножки зуба:
= 
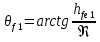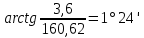
Угол головки зуба:
=
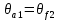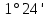
Проверяем соблюдение условий:
.
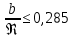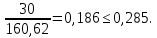
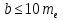
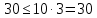
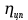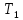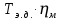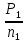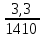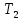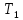
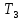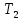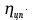
= 3,17 0,95 = 3,0 кВт; : = = 9550 = 9550 = 22,4 Нм. = = 22,4 5 0,96 = 107,4 Нм. = ∙ = 107,4 2,35 095 = 239,8 Нм.Таблица 1 -
| Валы | Частота вращения об/мин | Мощность, кВт | Крутящий момент, Н.м. | Передаточное отношение | К.П.Д. | |||||
| I |  | 1410 | Р1 | 3,30 | 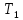| 22,4 | | 5,0 | 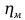 | 0,98 |
| II |  | 282 | Р2 | 3,17 | 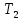| 107,4 | | 0,96 | ||
| | 2,35 | |||||||||
| III |  | 120 | Р3 | 3,0 | 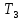| 239,8 | 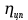| 0,95 | ||
2 Выбор материалов зубчатой передачи. Определение допускаемых контактных и изгибных напряжений
2.1 Выбор материалов для зубчатых колес
Шестерня – сталь 45; Dзаг более 120 мм; термообработка – улучшение; НВср1=215. [2, табл.7].
Колесо – сталь 45, Dзаг любой; термообработка – нормализация; НВср2=190. [2, табл.7].
2.2 Определение допустимых контактных напряжений
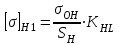
где σон – предел контактной выносливости, МПа, σон=2НВср+70. [2, табл.7].
Sн – коэффициент безопасности, Sн=1,1. [2, табл.7].
Кнл =1,0 – коэффициент долговечности.
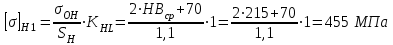
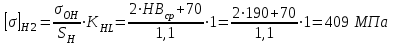
2.3. Определение допускаемых изгибных напряжений
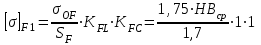
где σof – предел изгибной выносливости, МПа, σof= 1,75∙НВср. [2, табл.8].
Sf – коэффициент безопасности, Sf=1,7. [2, табл.8].
КFL =1,0 – коэффициент долговечности;
КFC – коэффициент учитывающий влияние двухстороннего;
приложения нагрузки, КFС =1,0. [2, табл.8].
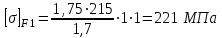
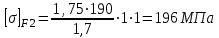
3 Расчет закрытой конической передачи с прямыми зубьями
3.1 Проектный расчет
Из условия контактной прочности находим ориентировочное значение среднего делительного диаметра шестерни:
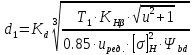, мм.где Т1 – крутящий момент на валу шестерни, Нм;
КНβ – коэффициент неравномерности распределения нагрузки по длине
зуба, зависящий от твердости зубьев передачи и расположения
колес относительно опор, КНβ = 1,1. [2, табл.10].
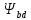– коэффициент ширины венца колеса по среднему делительному
диаметру шестерни,
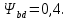[2, табл.11]. 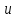– передаточное отношение проектируемой конической передачи; 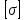Н – допускаемые контактные напряжения для материала колеса, как наиболее слабого звена передачи, МПа;
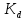– вспомогательный коэффициент, для стальных колес с прямым зубом
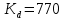. [2, табл.9]. 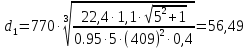мм. Ширину зубчатого венца колеса определяем по формуле:
b =
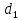· , ммb = 0,4 · 56,49 = 22,6 мм.
Находим внешние делительные диаметры шестерни:
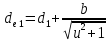, мм.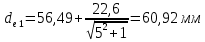 .Колеса:
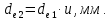
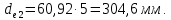
Полученные при расчете величины bи
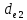округляем до стандартных значений, b = 45 мм и 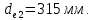Так как значение b, найденное расчетом составляет b=22,6, а по таблице b=45, то принимаем b=30 мм.Внешний окружной модуль передачи рассчитываем по формуле:
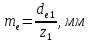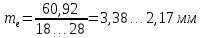. .Принимае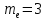м
мм.Число зубьев колеса определяем по формуле:
z2 =
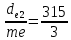= 105Принимаем z2=105.
z1 =
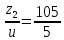= 21Принимаем z1=21.
Фактическое передаточное отношение:
Uф =
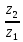= 105/21 = 5.Отклонение:
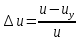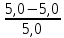= ∙ 100% = 0 % < 4%.Углы делительного конуса:
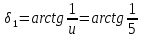=11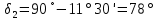°30' 30'Основные геометрические параметры определяем по формулам:
Внешний делительный диаметр:
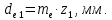
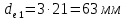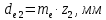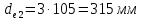. . .Внешний диаметр вершин зубьев:
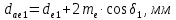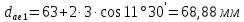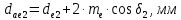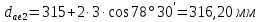. . . .Внешнее конусное расстояние:
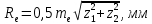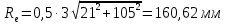. .Средний модуль:
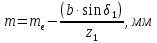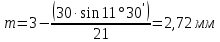. .Средний делительный диаметр:
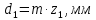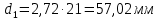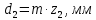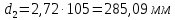. . . .Высота головки зуба:
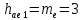мм.Высота ножки зуба:
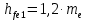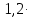= 3= 3,6 мм.Угол ножки зуба:
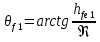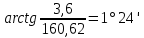
= Угол головки зуба:
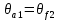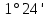
= Проверяем соблюдение условий:
.
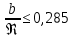