Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 603
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Правила выбора сечений
-
Сечения выбираются всегда перпендикулярно направлению движения жидкости; -
Сечения выбираются там, где известно максимальное число слагаемых уравнения Бернулли или там, где нужно что-то определить; -
В сечениях струйки жидкости должны быть параллельны друг другу, именно при таком условии справедливо уравнение Бернулли.
ВНИМАНИЕ!
-
Нельзя выбирать сечения на повороте трубы, при входе в трубу и т.д., то есть там, где скорость движения резко меняется по величине или по направлению и струйки искривляются.
-
В левой части уравнения стоит энергия того сечения, от которого на- чинается движение.
-
ЗАКОН СОХРАНЕНИЯ МАССЫ
Количество вещества, проходящее через поперечное сечение потока, можно измерить в единицах массы, объёма или веса. Это количество зависит, очевидно, от скорости движения, величины сечения и времени наблюдения.
1 1’
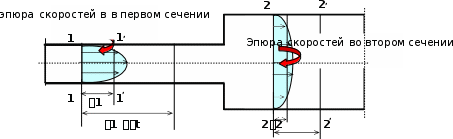
Согласно Рис.15, через сечение 1-1 за время t пройдет объём жидкости, равный объёму цилиндра 1-1-1-1,то есть V1=1s1t, и масса жидкости m1=11s1t.
2t
Рис. 15
Иллюстрация к выводу закона сохранения массы
На пути движения от начального сечения к конечному форма поперечных сечений потока может меняться самым причудливым образом, однако то мас- совое количество жидкости, которое прошло за время tчерез любое сечение, должно
остаться неизменным. Это следует из закона сохранения массы.
Для Рис. 15:
11s1t=22s2t. (26)
Поскольку время можно выбирать произвольно, удобно сравнивать ко- личества жидкости, проходящие за единицу времени (l с, 1 мин, 1 час и т.д.).
Количество жидкости, проходящее через сечение за единицу времени, называется расходом.
Q=s - объемный расход (27)
Qm=s=Q=m/t - массовый расход (28)
QG=gs=gQ=G/t - весовой расход (29)
Для жидкости плотность можно считать постоянной величиной. Это следует из закона Гука.
Закон Гука определяет связь между напряжением и объемной деформа- цией при всестороннем сжатии жидкости:
p=-E
Здесь E - модуль объёмной упругости жидкости, =V/V -относительное изменение объёма, V - первоначальный объем. Знак минус показывает, что при увеличении давления объём жидкости уменьшается.
Модуль упругости стали Eст=21011Па, а модуль упругости воды E=2109Па. Вследствие высокого модуля упругости жидкости сжимаются не- значительно. Так, при повышении давления на 10МПа, изменение объёма рав- но:
V p
V E
10 106
2 109
0,5 102
0,5%.
Поэтому чаще всего в гидравлических расчетах жидкость считают не- сжимаемой и плотность жидкости =m/V принимается величиной постоянной и независящей от давления:
Принимая =const, вместо (26) получим:
1s1=2s2=.......=Q=const. (30)
Уравнение (30) выражает закон постоянства объемного расхода по длине потока.
-
ЗАКОНЫ СОХРАНЕНИЯ МАССЫ И ЭНЕРГИИ ПРИ ДВИЖЕНИИ ГАЗА
При движении газа (расчет газопроводов) нужно учитывать, что плот- ность газа зависит от давления и температуры:
=p/RT. (31)
Это уравнение состояния газа (уравнение Клайперона). Здесь R – газовая постоянная, равная для воздуха 287дж/кгК.
В разных сечениях трубопроводной системы давление может отличаться на десятки атмосфер. Это приводит к существенному различию плотностей в сечениях газового потока и, как следствие, к различию объёмных расходов.
При движении газа в сечениях потока сохраняется массовый расход!
Qm= 11s1=22s2=……=ii
si=const (32)
Как известно, капельная жидкость в сечении обладает потенциальнойикинетическойэнергией.
Газы обладают потенциальной,кинетическойивнутреннейэнергией.
Внутренняя энергия газа зависит от температуры.
1
1
Для самого общего политропного процесса закон сохранения энергии для единицы веса (1н) газа имеет вид:
z1
p1
1 g
n
p1
1 1 g
2
1 ... 9 10 11 12 13 14 15 16 ... 25
11 z2
2g
p2
2 g
n
p2
1 2 g
222
2g
h1 2 ,
где z – удельная потенциальная энергия положения; p/g - удельная по- тенциальная энергия давления; p/(g(n-1))=RT/(g(n-1))-внутренняя энергия;
2/2g –удельная кинетическая энергия; h1-2- потери энергии; n –показатель по- литропы.
Если при движении газа по трубам вследствие теплообмена с окружаю- щей средой температура по длине не изменяется, то имеет место изотермиче- ский процесс (T=const). При этом внутренняя энергия в сечениях трубопровода остается постоянной.
Уравнение Бернулли при изотермическом течении газа имеет такой же вид, как и для несжимаемой жидкости (плотности газа в сечениях разные!):
p 2 p 2
z1 1
1 1 z2 2 22 h1 2 . (33)
1 g 2g 2 g 2g
-
РАСЧЕТ ТРУБОПРОВОДОВ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Большинство гидродинамических задач нефтегазовой практики связано с движением жидкости по различного рода трубопроводным системам. При этом необходимо знать количествопротекающей жидкости или газа (расход) и энергетические характеристики, зависящие от давления и положения жид- кости в поле силы тяжести (высот z). Часто возникает и обратная задача – при известном расходе и энергетических характеристиках определить диаметртрубопровода. Далее на конкретных примерах рассмотрены способы решения этих и некоторых других задач.
-
ОПРЕДЕЛЕНИЕ СИЛЫ ИЛИ ДАВЛЕНИЯ
Определить силу R, которую нужно приложить к поршню насоса диамет- ром D=65мм, чтобы подавать в бак бензин (плотность = 765кг/м3, кинемати- ческий коэффициент вязкости = 0,4сСт) с постоянным расходом Q = 2,5л/с. Высота подъёма жидкости в установке H0= 10м, показание манометра рм0
=0,15МПа. Размеры трубопровода l =60м, d =30мм; его эквивалентная шерохо- ватость э=0,03мм; коэффициент сопротивления вентиля в=5,5.
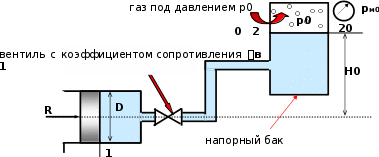
Рис. 16
Схема к задаче