Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 614
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 30
Перед подземным ремонтом газовую скважину “задавили”, залив её ствол до устья (до поверхности земли) водой (t=20C). Затем в скважину лебёдкой спус- тили насосно-компрессорные трубы, по которым при эксплуатации скважины поступает из пласта газ. Длина спущенных труб равна l, внешний диаметр D, толщина стенки , вес одного метра длины q.
Определить максимальное усилие на крюке лебедки для двух случаев:
-
нижний конец труб открыт – четные варианты;
2)нижнийконецтрубзаглушен –нечетные варианты.
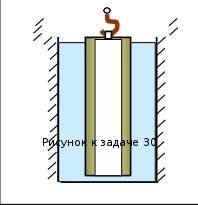 Указания
Указания-
Сила на крюке лебедки равна алгеб- раической сумме сил, действующих на трубы. -
На трубы действует собственный вес и подъёмная сила (сила Архи- меда). -
На рисунке изображена ситуация, когда нижний конец труб заглушен и площадь действия выталкиваю- щего давления жидкости равна площади круга диаметром D.
Таблица вариантов
| Вар-нт | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| D, мм | 73 | 114 | 146 | 168 | 194 | 245 | 273 | 299 | 73 | 146 |
| l, км | 1,0 | 1,4 | 1,1 | 1,5 | 1,6 | 0,9 | 1,0 | 0,8 | 1,3 | 1,7 |
| ,мм | 5,5 | 4 | 5 | 6 | 7 | 9 | 10 | 10 | 4 | 5 |
| q,н/м | 94 | 96 | 130 | 150 | 165 | 195 | 198 | 200 | 94 | 125 |
РАЗДЕЛ5
 МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ГИДРОДИНАМИКИ
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ГИДРОДИНАМИКИ

Методика решения всех задач гидродинамики, по существу, сводится к сле- дующему:
-
Записать в общем виде уравнения, выражающие законы сохранения массы и энергии при движении жидкости или газа. -
Определить слагаемые этих уравнений, согласно исходным данным. -
Решить полученную систему уравнений относительно неизвестной величи- ны.
ЗАКОНЫ СОХРАНЕНИЯ - фундаментальные физические соотношения, на основании которых выводятся частные законы. В современной науке извест- но более десяти законов сохранения, большинство из них относится к ядерной физике. При решении гидродинамических задач широко используются сле- дующие:
-
Закон сохранения массы. -
Закон сохранения энергии.
Эти два закона являются следствием того очевидного факта, что время и место действия не могут сами по себе изменить ход физического процесса (при одинаковых начальных условиях эксперимент будет проходить совершенно одинаково в Ухте и в Лондоне, сегодня и месяц назад).
-
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Энергия - запас работы, которую может совершить тело, изменяя свое состоя- ние.
Работа - скалярное произведение силы на перемещение под действием этой си- лы. На практике величина работы используется для характеристики механизма или технического устройства.
Энергия - это невостребованная работа, математическая абстракция, фор- мула, по которой можно вычислить максимальную работу. В реальных ус-
ловиях функционирования конкретного механизма часть энергии теряется и переходит в тепло.
Отношение полученной работы к затраченной энергии есть коэффи- циент полезного действия механизма.
Энергия проявляется во множестве различных форм. Она может быть оп- ределена таким способом, что при любом превращении системы полная энер- гия сохраняется. Однако для системы, которая не претерпевает никаких изме- нений, разговор об энергии беспредметен. Только при переходе из одной фор- мы в другую или из одного места в другое представление об энергии становит- ся очень полезным как средство для решения практических задач.
Механическаяэнергияразделяется на кинетическуюипотенциаль-
ную:
E=EK+EП.(14)
Кинетическая энергия
Кинетическаяэнергия- это форма энергии, связанная с механическим движением.
Кинетическая энергия EKчисленно равна работе, которая совершается при уменьшении скорости тела от uдо нуля.
EK=mu2/2. (15)
Потенциальная энергия
Потенциальными называют неподвижные формы энергии, которые по- тенциально можно превратить в энергию движения. К таким формам относят энергию, запасенную в деформированном теле или в результате смещения тел в некотором силовом поле (электрическом, магнитном или гравитационном). По- тенциальная энергия жидкости или газа разделяется на два вида:
-
потенциальная энергия положения; -
потенциальная энергия давления. Потенциальная энергия положения
Твёрдое, жидкое или газообразное тело массой m занимают определённое
положение в поле силы тяжести (Рис.12).
Горизонтальная плоскость отсчета Eполож.выбирается произвольно. Это связано с тем, что нас интересуют только изменения потенциальной энергии,
а
не её абсолютная величина. При переходе тела из положения 1 в положение 2
изменение потенциальной энергии Eполож будет равно:
Eполож= mgz2- mgz1=mg(z2-z1) =mgz -плоскость отсчета 0-0
2 1 1 2
Eполож=mg(-z) - mg(-z)=mg(z -z)= mgz -плоскость отсчета 0’-0’
Изменение потенциальной энергии Eполож не зависит от выбора плоскости отсчета.
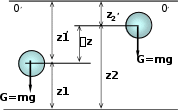
0 0
0-0, 0’-0’ - плоскости отсчета Eполож.
Рис.12
Иллюстрация к выводу формулы потенциальной энергии положения
A=Gz = mgz- работа силы тяжести;
Eполож.=mgz - потенциаль- ная энергия положения, чис- ленно равна работе, которую совершает сила тяжести при падении тела с высоты z. Ес- ли тело расположено выше плоскости отсчета, высота zберется со знаком (+), если ниже - со знаком (-).
Итак, потенциальная энергия положения жидкости Eполож. равна:
Eполож = mgz. (16)
Потенциальная энергия давления
Другой вид потенциальной энергии связан с деформацией тел. Для твер- дого тела такой вид энергии запасается в сжатой пружине, для текучих тел (жидкостей и газов) такой вид энергии называется потенциальной энергией давления.
Покоящаяся и движущаяся жидкость находится в деформированном (сжатом) состоянии под действием поверхностных и массовых сил, при этом в жидкости появляется энергия упругой деформации, пропорциональная величи- не напряжений сжатия (давлений) в жидкости. При расширении жидкости энер- гия упругой деформации превращается в работу (Рис.13).