Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 605
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
р–избыточное давлениеx
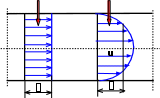
Рис. 13
Иллюстрация к выводу формулы по- тенциальной энергии давления
F=ps- сила, действующая на пор- шень со стороны сжатой жидкости; s=D2/4 - площадь сечения поршня;
р- давление в жидкости;
A =Fx =psx =pV=pm/ - работа по перемещению поршня, совершаемая за счет наличия в жидкости давления р.
V - изменение объёма жидкости в ре- зультате расширения при движении поршня.
Итак, потенциальная энергия давления жидкости Eдавл равна:
Eдавл= pm/ (17)
-
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ИДЕАЛЬНОЙ ЖИДКОСТИ Идеальная жидкость - жидкость без вязкости и абсолютно несжимае-
мая. В такой гипотетической жидкости отсутствуют силы трения и не тратится энергия на работу по их преодолению, а также плотность жидкости есть вели- чина постоянная в любом сечении потока. Такое приближение хорошо работает при рассмотрении движения жидкости в медленных потоках или длинных тру- бах (до тех пор, пока не интересуются тем, что происходит у стенок) и позволя- ет в первом приближении решать практические задачи.
Итак, полный запас энергии объёма жидкости массой m относительно нулевого уровня (плоскости сравнения 0-0) равен:
E=mgz+m p/+mu2/2. (18)
Для идеальной (невязкой) жидкости, в которой не происходит потерь энергии при движении, в произвольных сечениях 1-1 и 2-2 энергии должны быть равны:
гий.
E1=E2;
1 2
mgz1+m p1/+mu2/2 = mgz2+mp2/+mu2/2. (19)
Уравнение (19) можно представить как закон сохранения удельных энер-
Термин удельная энергия предполагает отношение полной энергии к
некоторому количеству вещества - объёмному, массовому или весовому.
Энергия, отнесённая к весу жидкости, называется напором. Напор из- меряется в метрах. После деления всех членов уравнения (22) на вес жидкости G=mg, оно принимает вид:
g
g
p1 u2
p u2
z1
1 z2 2 2
. (20)
Уравнение (20) называется уравнением Бернулли. Оно было получено в
1738 году швейцарским математиком и механиком Даниилом Бернулли.3
При расчете гидроприводов, газо- и нефтепроводов уравнение (20) ис- пользуют обычно в виде баланса энергий, отнесенных не к весу, а к объему протекающей жидкости V=m/:
u2 u2
g z1 p1 1 g z2 p2 2
. (21)
2 2
Все слагаемые уравнения (21) имеют размерность давления и называются соответственно:
gz1, gz2- весовые давления в центрах тяжести сечений 1-1и 2-2;
р1,р2- статические давления в центрах тяжести сечений 1-1и 2-2;
1 2
u2/2, u2/2 - динамические давления в центрах тяжести сечений 1-1и 2-2.
Статическое давление - это напряжение сжатия в жидкости, которое по- является в результате действия на жидкость сжимающих сил.
Динамическое давление - давление жидкости на преграду при её оста- новке и превращении кинетической энергии в энергию давления.
-
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ РЕАЛЬНОЙ ЖИДКОСТИ
При переходе от идеальной жидкости к реальной необходимо учесть наличие вязкости (сил межмолекулярного взаимодействия при сдвиге) как ме- жду жидкостью и стенкой, так и между отдельными слоями жидкости. Вслед- ствие этого эпюра скоростей в сечении потока получается неравномерной (эпюра 2, Рис.14).
3 Даниил Бернулли (1700-1782) -швейцарский ученый, разрабатывал законы механики жид- костей.
эпюра 1 эпюра 2
u-местная скорость в сечении dsэле- ментарной струйки;
-средняя скорость в сечении потока жидкости или скорость движения всех струек идеальной жидкости (эпюра 1). Q=uds=s-объёмный расход в сече- нии sпотока жидкости.Рис. 14
Эпюра скоростей в сечении потока жидкости
Определим действительную кинетическую энергию потока как сумму ки- нетических энергий отдельных струек:
EK=dmu2/2=dQu2/2= udsu2/2==t dsu3/2. (22)
На практике удобно определять кинетическую энергию потока по сред- ней скорости. Докажем, что действительная кинетическая энергия потока EKбольше кинетической энергии m2/2, определяемой по средней скорости . Для этого представим местную скорость u как сумму средней скорости и некото- рой знакопеременной добавки : u =+ и вычислим отношение кинетических энергий:
3
E t ( ) ds (3 32 3 2 3 )ds
K
m 2 / 2
t Q 2
3 2
Q 2
(3 3 2 )ds
3 s
(1 2
s)ds
1
3 2 ds s 2
1;Здесь учтено, что при суммировании те слагаемые, куда входит знакопе- ременная добавка в нечетной степени, равны нулю.
Корректив кинетической энергии называется коэффициентом Кориоли-
са.
Итак:
Чембольшенеравномерностьместныхскоростей в сечении потока
(больше ),тембольшекорректив кинетической энергии ..
При ламинарномрежименеравномерность местных скоростей макси- мальная и расчетное значение =2. При турбулентномрежиме вследствие
перемешивания частиц скорости в сечении выравниваются и =1,1 -1,2..Для практических расчетов при турбулентном режиме принимается =1.
Наличие вязкости приводит к появлению в потоке жидкости при ее дви- жении сил трения, которые направлены против движения. На их преодоление затрачивается энергия жидкости.
Потерянная энергия, отнесенная к весу жидкости, называется потерями напора по длине и обозначается hдл.
Кроме того, поток жидкости при своем движении претерпевает дефор- мацию, которая вызывается установкой трубопроводной арматуры (краны, вен- тили, муфты, шайбы и др.), а также поворотами потока, внезапным расширени- ем в сужением.
Потери энергии в такого рода препятствиях называются местными и обо- значаются hм .
Суммарные потери удельной энергии h1-2равны:
h1-2= hдл+ hм. (23)
С учетом вязкости и деформации потока уравнение Бернулли для реаль- ной жидкости принимает вид:
p
2 p 2
z1 1 11 z2 2 22 h12
. (24)
g 2g g 2g
Таким образом, уравнение Бернулли представляет собой закон сохране- ния энергии для движущейся жидкости:
Суммарнаяэнергияжидкостивначальномсечении(потенциальная плюс кинетическая) равна суммарной энергии жидкости в конечном сеченииплюспотериэнергии.
Другими словами:
Начальная энергия всегда равна сумме энергии, что еще осталась, и энер- гии, что по пути потерялась.
Если между сечениями потока 1-1 и 2-2 имеется источник энергии (на- пример, насос), энергия жидкости в месте установки насоса скачком возрас- тает и закон сохранения энергии принимает вид:
p1 1 2
g
2g
g
2g
p 2
Hнас. z1
1 z2 2
2 2
h12
, (25)
где Hнас.- удельная энергия, которую насос забирает у приводного двигателя и передает жидкости (напор насоса).
Суммарная энергия жидкости в начальном сечении (потенциальная плюс кинетическая) плюс та энергия, что добавилась в насосе, равна сум- марной энергии жидкости в конечном сечении (той, что осталась) плюс по- тери энергии.
Уравнение Бернулли в любой форме справедливо для тех сечений потока, где струйки не искривляются и не возникает сил инерции.