Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 617

Скачиваний: 8

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

ОСНОВНОЕ СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

ОСНОВЫ ГИДРОСТАТИКИ

МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ГИДРОСТАТИКИ

МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ГИДРОДИНАМИКИ

КОНТРОЛЬНЫЕ ЗАДАЧИ ПО ГИДРОДИНАМИКЕ

ПРИЛОЖЕНИЯ

ОГЛАВЛЕНИЕ


Так как число Рейнольдса Re>Reкр(2,65105>2300), то коэффициент тре-

ния рассчитывался по формуле (38).

По условию кинематический коэффициент вязкости задан в сантистоксах

(сСт). 1сСт = 10-6м2/с.

    • Коэффициент Кориолиса 1 в сечении 1-1

Re4Q

1 D

4 2,5 103

3,14 0,065 0,4 106

1,22 105 ;

Так как режим движения в сечении 1-1турбулентный, то 1=1.

    • Сила на штоке

R 3,32 103

765 9,8 (10

0,15 106

765 9,8

60 (0,71 103 )2 (2,5 103 )2

(0,021 0,03 9,53 (3,32 103 )2

) (0,71 103 )2 2 9,8 ) 1558 Н




ОПРЕДЕЛЕНИЕ РАСХОДА ЖИДКОСТИ

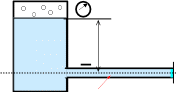Топливо (=819кг/м3, динамический


1

0


Рис. 17

Схема к задаче

рv 1 H


l,d

коэффициент вязкости =1,510-3Пас)

вытекает в атмосферу из резервуара с постоянным уровнем H=5,6м и избы-

0 2 точным давлением на поверхности

жидкости рм=10кПа по горизонталь-

2ному трубопроводу (l=30м, d=80мм, трубы сварные, бывшие в употребле- нии, =3).

Определить расход.



ВНИМАНИЕ!

Поскольку все необходимые пояснения и теоретические основы приме- нения уравнения Бернулли были подробно сделаны при решении задачи 1, за- кон сохранения энергии для данной задачи выводится без подробных поясне- ний.

Решение

  1. Выбираем два сечения 1-1и 2-2, а также плоскость сравнения 0-0и записы- ваем в общем виде уравнение Бернулли:


2g
g
2g
p   2 p   2


g
z1 1

1 1 z2 2 22 h1 2 .

Здесь р1и р2– абсолютные давления в центрах тяжести сечений; 1и 2– средние скорости в сечениях; z1и z2– высоты центров тяжести сечений относи- тельно плоскости отсчета 0-0; h1-2–потери напора при движении жидкости от первого до второго сечения.

  1. Определяем слагаемые уравнения Бернулли в данной задаче.

  • Высоты центров тяжести сечений: z1=H; z2=0.

  • Средние скорости в сечениях: 2= Q/s2=4Q//d2;

1= Q/s1. Так как s1>>/s2, то 1<<2и можно принять 1=0.

  • Коэффициенты Кориолиса 1 и 2 зависят от режима движения жидкости. При ламинарном режиме =2, а при турбулентном =1.

  • Абсолютное давление в первом сечении р1=рм+рат, рм– избыточное

(манометрическое) давление в первом сечении, оно известно.

  • Абсолютное давление в сечении 2-2 равно атмосферному рат, так как жидкость вытекает в атмосферу.

  • Потери напора h1-2складываются из потерь напора на трение по длине потока hдли потерь на местные гидравлические сопротивления hм.

h1-2=hдл+ hм.

  • Потери по длине равны


l 2
l Q2

hдл d 2g d s2 2g.

  • Местные потери напора равны

hм=  2/(2g)=  Q2/(s22g); где задано по условию

  • Суммарные потери напора равны

h1-2= (l/d+) Q2/(s22g);

  1. Итак, подставляем определенные выше величины в уравнение Бернул- ли и получаем закон сохранения энергии для нашей задачи:

рм

pат

pат

2 Q2 l Q2




H g

0 0

g s

2 2g ( d

) s2 2g.


2
Сокращаем слагаемые с атмосферным давлением, убираем нули и приво-

дим подобные члены. В результате получим:

рм l Q2




H g ( d 2 ) s2 2g. (43)
Это расчетное уравнение для определения расхода жидкости. Оно пред- ставляет собой закон сохранения энергии для данной задачи. Расход входит в правую часть уравнения непосредственно, а также в коэффициент трения  че- рез число Re (Re=4Q/(d)!

Не зная расход, невозможно определить режим движения жидкости и вы- брать формулу для . Кроме этого, при турбулентном режиме коэффициент трения зависит от расхода сложным образом (см. формулу (38)). Если подста-

вить выражение (38) в формулу (43), то полученное уравнение не решается ал- гебраическими способами, то есть является трансцендентным8. Такие уравне- ния решаются графическим способом или численно с помощью ЭВМ (чаще всего методом
итераций).

Численный способ решения

Задача решается методом последовательных приближений - методом итераций9. Как известно из математики, для применения этого метода необхо- димо представить уравнение (54) в виде: аргумент равен функции от аргу-мента- Q=(Q).



Q(Q);

(44)



Порядок расчета

  • Задаемся некоторым начальным значением oкоэффициента трения и значением коэффициента Кориолиса о. Если в результате анализа ис- ходных данных можно предположить ламинарный режим (высокая вяз- кость жидкости), то o=64/Reкр, и о=2; если турбулентный (малая вяз- кость и значительная шероховатость труб), то o=0,11(э/d)0,25 и о=1 (предполагается режим квадратичных сопротивлений).

  • Определяется правая часть уравнения (44) - функция (Q), то есть на- чальное значение расхода жидкости Qo.

  • Определяется число Reo=4Qo/(d, уточняется режим движения и оп- ределяется значение 1коэффициента трения по уточненным формулам:




Re d ρ Qо 4 d ρ Qо

4 ρ

оη π d2 η

π d η

Reо< 2300 1=64 /Reо,1=2.

Reо> 2300 1=0,11(68/Reо+э/d)0,25, 1=1.

  • Определяется правая часть уравнения (44) - функция (Q),то есть после- дующее значение расхода жидкости Q1.





8 Трансцендентныйпроисходит от лат. transcendo –выхожу за пределы.

9 Итерация(от латинского iteratio - повторение) - повторное применение какой-либо мате- матической операции.

Смотрите также файлы