Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 611
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Сравниваются расходы Q1и Qо. Если они отличаются на заданную точ- ность, расчет прекращается. Если нет, то повторяются пункты 35 до тех пор, пока последующее и предыдущее значение расхода не совпадут с за- данной точностью.
Принимаем для стальных умеренно заржавленных труб э= 0,2мм. Судя по исходным данным – жидкость маловязкая и можно предположить турбу- лентный режим движения.
В нашей задаче o=0,11(э/d)0,25 =0,11(0,2/80)0,25=0,025; Qo=0,0159; Re0=1,38105; 1=0,11(68/1,38105 +0,2/80)0,25= 0,026; Q1=0,0157. Re1=1,36105;
2=0,11(68/1,36105 +0,2/80)0,25= 0,026; Q2=0,0157
Q1= Q2= Q= 0,0157м3/с - расчетное значение расхода.
В нашем примере после второго приближения расчет можно закончить. Метод итераций - один из наиболее распространенных методов числен-
ного решения уравнений, легко реализуется на ЭВМ. В случае ламинарного режима движения:
=64/Re=64d/(4Q)
и уравнение (43) превращается в квадратное уравнение относительно расхода.
pм Q2 8 128Q l
H g 2 d4 g( ) d4 g
(45)
Корни уравнения (45) легко определяются.
1 ... 12 13 14 15 16 17 18 19 ... 25
Графический способ решения
Решить любое уравнение - это значит найти то значение неизвестной ве- личины, при котором левая часть уравнения равна правой.
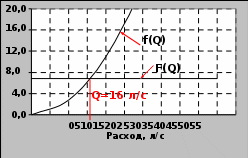
Графический способ основан на построении графиков функций левой и правой частей уравнения (43) и нахождении точки их пересечения. При этом последовательно задаются рядом значений расхода Q, вычисляя при каждом значении Q число Re, , f(Q), F(Q). В данном случае F(Q) обозначена левая часть уравнения (43).
Последовательность вычисления коэффициента трения и коэффициента Кориолиса на каждом шаге остается прежней, а именно: Последовательность вычисления и .
Re
d Q4d Q4
d2 d
Re< 2300 =64 /Re,.=2.
Re> 2300 =0,11(68/Re+э/d)0,25, .=1.
Расчеты и построение графиков очень удобно выполнять на ЭВМ с по- мощью электронных таблиц (Microsoft Excel). Ниже представлена расчетная таблица и графики.
| Q,л/с | 0,0001 | 10 | 20 | 30 | 40 | 50 |
| Re | 0,869 | 86943 | 2E+05 | 3E+05 | 3E+05 | 4E+05 |
| | 0,327 | 0,026 | 0,026 | 0,025 | 0,025 | 0,025 |
| f(Q) | 2,6E-09 | 2,801 | 10,96 | 24,45 | 43,29 | 67,47 |
| F(Q) | 6,84 | 6,84 | 6,84 | 6,84 | 6,84 | 6,84 |
-
ОПРЕДЕЛЕНИЕ ДИАМЕТРА ТРУБОПРОВОДА И КАВИТАЦИОННЫЙ РАСЧЕТ
По сифонному сливу (l= 50м, d= ?, шероховатость трубопровода
э=0,06мм) подается топливо (=840кг/м3, =5,510-6м2/с) с расходом
Q = 0,01м3/с при разности отметок уровней в резервуарах H=1,38м.
На сливе имеется фильтр для светлых нефтепродуктов, два колена и вен- тиль, который полностью открыт. Даны также высоты h0=3м и b=2м., давление насыщенных паров при температуре перекачки рн.п.= 3кПа, рат=105Па.
Определить диаметр трубопровода и проверить условие нормальной ра- боты сифона.
h0
0 1 10
H
опасное сечение 3-3
 Осторожно -
Осторожно -кавитация!
2 2 b
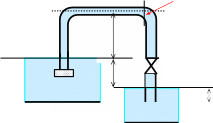
Рис. 19
Схема к задаче
Опасное сечение то, где давление меньше атмо- сферного и минимально
Поскольку все необходимые пояснения и теоретические основы приме- нения уравнения Бернулли были подробно сделаны при решении задачи 1, за- кон сохранения энергии для данной задачи выводится без подробных поясне- ний. Сначала определим диаметр трубопровода.
Определение диаметра трубопровода
-
Выбираем два сечения 1-1 и 2-2, а также плоскость сравнения 0-0 и за- писываем в общем виде уравнение Бернулли:
2g
g
2g
p 2 p 2
g
z1 1
1 1 z2 2 22 h1 2 ,
где р1и р2– абсолютные давления в центрах тяжести сечений; 1и 2– средние скорости в сечениях; z1и z2– высоты центров тяжести сечений относи- тельно плоскости отсчета 0-0; h1-2–потери напора при движении жидкости от первого до второго сечения.
-
Определяем слагаемые уравнения Бернулли в данной задаче.
-
Высоты центров тяжести сечений: z1=0;z2=-H; -
Средние скорости в сечениях: 1=Q/s1;2= Q/s2; тр= Q/s.
Так как s1>>/s, и s2>>/s, то 1<<три 2<<тр; можно принять
1=2=0 по сравнению со скоростью движения в трубопроводе.
Другими словами, слагаемое h1-2, которое пропорционально тр, много больше слагаемых 112/2gи 222/2gи ими можно пренебречь.
-
Абсолютное давление в первом сечении равно атмосферному,
р1= рат;
-
Абсолютное давление в сечении 2-2 равно атмосферному, р2= рат.
-
Потери напора h1-2складываются из потерь напора на трение по длине потока hдли потерь на местные гидравлические сопротивле- ния hм
h1-2= hдл+ hм.
-
Потери по длине равны
l 2 l Q2
hдл d 2g d s2 2g. (принимаем тр= ).
-
Местные потери напора равны:
hм= 2/(2g)= Q2/(s22g); где =ф+ 2пов+в+ вых.
ф=1,7; пов= 0,23; в= 0,15; вых= 1 (Приложение 6).
=1,7 + 0,46 + 0,15 +1 =3,31.
-
Суммарные потери напора равны:
h1-2= (l/d+) Q2/(s22g).
-
Подставляем определенные выше величины в уравнение Бернулли и решаем его относительно диаметра.
В нашей задаче закон сохранения энергии имеет вид:
H ( l
d
) Q2 . (46)
s2 2g
Это расчетное уравнение для определения диаметра трубопровода.. Оно представляет собой закон сохранения энергии для данной задачи. Диаметр вхо- дит в правую часть уравнения непосредственно, а также в коэффициент трения
через число Re(Re=4Q/(d)!
Не зная диаметр, невозможно определить режим движения жидкости и выбрать формулу для . Кроме этого, коэффициент трения зависит от диаметра сложным образом (см. формулы (37) и (38)). Если подставить эти выражения в формулу (46), то полученное уравнение не решается алгебраическими способа- ми (является трансцендентным). Такие уравнения решаются графическим спо- собом или численно с помощью ЭВМ (чаще всего методом деления отрезка по- полам).
Графический способ решения
Решить любое уравнение - это значит найти то значение неизвест- ной величины, при котором левая часть уравнения равна правой.
Графический способ основан на построении графиков функций левой и правой частей уравнения (46) и нахождении точки их пересечения. При этом последовательно задаются рядом значений диаметра d, вычисляя при каждом значении d число Re, , f(d), F(d). В данном случае F(d) обозначена левая часть уравнения (46).
Последовательность вычисления коэффициента трения на каждом шаге остается прежней, а именно:
Последовательность вычисления :