Файл: Учебное пособие по решению задач Допущено Учебно методическим объединением вузов Российской Федерации по высшему.docx

Re< 2300 _{=64 /Re}

^{Re> 2300}  =0,11(68/Re+_э/d)^0,25

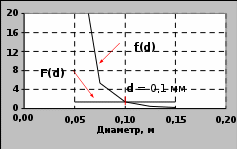
Ниже представлена расчетная таблица и графики, выполненные на ЭВМ с помощью электронных таблиц (MicrosoftExcel).

d	0,05	0,075	0,10	0,13	0,15
Re	4,63E+04	3,09E+04	2,32E+04	1,85E+04	1,54E+04
	2,50E-02	2,57E-02	2,68E-02	2,79E-02	2,90E-02
f(d)	37,4644	5,35238	1,38307	0,49048	0,21179
F(d)	1,38	1,38	1,38	1,38	1,38

Кавитационный расчет сифона

Явление кипения жидкости при давлениях меньших атмосферного и рав- ных давлению насыщенного пара, при нормальных температурах (10, 20,30,.....), сопровождающееся схлопыванием пузырьков пара в областях по- вышенного давления, называется кавитацией.

Давление насыщенного пара зависит от рода жидкости и температуры


14000
(Приложение 8).

---

50
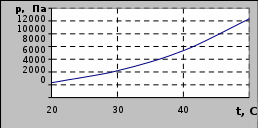
Рис. 21. Зависимость давления насыщенного пара воды от температуры

На Рис.21 показана зависимость насыщенного пара воды от температуры. Примерно такой же вид имеет такая зависимость для других жидкостей. Для того, чтобы вода закипела при 20С, необходимо создать очень низкое давление

– 2300Па.

Кавитация - вредное явление. Рассмотрим следствия кавитации на приме- ре работы сифона.

Пузырьки пара, выделяющиеся при кавитации, разрывают межмолеку- лярные связи, поток жидкости при этом теряет сплошность, столб жидкости на восходящей линии сифона и процесс всасывания прекращается. Кроме того, пу- зырьки пара, продвигаясь вместе с жидкостью дальше на нисходящую линию сифона, где давление больше давления насыщенного пара, лопаются.

При схлопывании пузырька на твердой поверхности трубы жидкость, уст- ремившаяся в освободившееся пространство, останавливается. При этом ее ки- нетическая энергия превращается в потенциальную и происходят местные гид- равлические удары. Это явление сопровождается существенным ростом давле- ния и температуры и приводит к разрушению материала поверхности.

Поскольку давление насыщенного пара при обычных температурах меньше атмосферного, сечения, где давление меньше атмосферного, считаются опасными с точки зрения возникновения кавитации.

В инженерной практике существует правило:

НЕ ДОПУСКАТЬ КАВИТАЦИИ!

Для этого необходимо, чтобы в сечениях потока, где давление меньше атмосферного, было выдержано условие: давление в жидкости больше дав- ления насыщенного пара.

р>p_н.п.. (47)

Это условие отсутствия кавитации.
Проверяем условие нормальной работы сифона

---

Для этого необходимо определить давление в опасном сечении 3-3и сравнить его с заданным по условию давлением насыщенного пара жидкости.

1. 
   Определяем давление в сечении 3-3 из уравнения Бернулли, составленно- го для сечений 1-1 и 3-3.
   

p   ² p   ²

• 
  z₁и z₃– высоты центров тяжести сечений относительно плоскости отсчета 0-0;
  
• 
  h_1-3–потери напора при движении жидкости от первого до второго сечения.
  

Определяем слагаемые уравнения Бернулли в данной задаче.

• 
  Высоты центров тяжести сечений: z₁=0; z₂=h₀;
  
• 
  Средние скорости в сечениях: ₃=Q/s=4Q//d²;
  

₁=Q/s₁.Так как s₁>>s₃, то ₁<<₃и можно принять ₁=0.

• 
  Коэффициенты Кориолиса ₁и ₂зависят от режима движения жид- кости. При ламинарном режиме =2, а при турбулентном =1.
  
• 
  Абсолютное давление в первом сечении р₁=р_ат,
  
• 
  Абсолютное давление в сечении 3-3 неизвестно и подлежит определе- нию..
  
• 
  Потери напора h_1-3складываются из потерь напора на трение по дли- не потока h_дли потерь на местные гидравлические сопротивления  h_м:
  

---

h_1-3= h_дл+ h_м.

• 
  Потери по длине равны:
  

l
h_дл   ⁰

d

 ^ 2   

2g

( l  ( H  h₀  b )d

_Q2

^ s^2 2g^,

где l₀– длина трубопровода от начала до сечения 3-3. l₀= 50-(1,38+3+2) = 43,62;

• 
  местные потери напора равны:
  

 h_м= ₀ ²/(2g)=  ₀ Q²/(²2g); где  ₀=_ф+ _пов.

_ф=1,7; _пов= 0,23; (Приложение 6).

 ₀=1,7 + 0,23 =1,93.

• 
  Суммарные потери напора равны:
  

h_1-2= (l₀/d+₀) Q²/(s²2g).

Итак, подставляем определенные выше величины в уравнение Бернулли.В нашей задаче закон сохранения энергии имеет вид:

p p ^

 Q² _{l Q}²

^ат  0  h₀ ³ 

 ( ⁰  _₀ ) .

  g

  g

s²  2g ^d

s²  2g

---

Убираем нули, приводим подобные члены и выражаем давление р₃.

В результате получим:

p_{3 }

  g

^pат

  g

 h₀ 

_Q2


s²  2g

 (  ^l0

d

 _   ). (48)

Из уравнения (48) определяем давление р₃. Значение коэффициента тре- ния определено ранее и равно 0,0268 (см. таблицы),  = 1 (режим турбулент- ный), =d²/4 = 3,140,1²/4=7,8510^-3м².

10⁵

0,01²

43 ,62

р₃  840  9,8  (_{840  9,8}  3  _{(7,85 10 3 )2  2  9,8}  (0,0268

0,1

 2,93 ) 65300 Па

Давление насыщенного пара равно 2 кПа. Так как 65,3 >> 2, то сифон будет работать.

7. 
   РАСЧЕТ ГАЗОПРОВОДОВ
   

При решении задач на расчет газопроводов нужно учитывать, что плот- ность совершенного¹⁰ газа зависит от давления и температуры: =p/RT

Это уравнение состояния газа (уравнение Клайперона). Здесь R – газовая постоянная, равная для воздуха 287дж/кгК.

В разных сечениях трубопроводной системы давление может отличаться на десятки атмосфер. Это приводит к существенному различию плотностей в сечениях газового потока и, как следствие, к различию объёмных расходов.

При движении газа в сечениях потока сохраняется массовый расход!

Q_m= ₁₁₁=₂₂₂=……=_i_i_i=const (49)

Как известно, капельная жидкость в сечении обладает потенциальной и кинетической энергией.

Газы обладают потенциальной, кинетической и внутренней энергией.

Внутренняя энергия газа зависит от температуры и вида процесса, по которому измененяется его состояние.

Если при движении газа по трубам вследствие теплообмена с окружающей сре- дой температура по длине не изменяется, то имеет место изотермический процесс (T=const). При этом внутренняя энергия в сечениях трубопровода ос- тается постоянной. Уравнение Бернулли при изотермическом течении газа име- ет такой же вид, как и для несжимаемой жидкости, за исключением того, что в сечениях потока разная плотность:

p   ² p   ²

---