ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 267
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
A(t) высокочастотного колебания S(t) = A(t)cos ω0t, другими словами в создании на выходе детектора низкочастотного колебания, повторяющего огибающую A(t). Задача детектора – это выделение сигнала SΩ, представленного на рисунке 7.5 как:
SΩ (t) = KA(t).
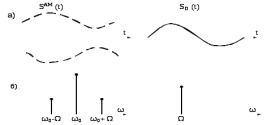
Рис.7.5 – Диаграммы сигналов на входе SАМ (t) и выходеSΩ (t) детектора: а) временные; б) спектральные
На рисунке 7.6 приведена структурная схема детектора, состоящая из нелинейного элемента и фильтра нижних частот. Временные и спектральные диаграммы напряжений на рисунке подчеркивают тот факт, что модулирующего сигнала в спектре АМ-сигнала нет, и задача нелинейного элемента, именно его выделить из АМ-сигнала.
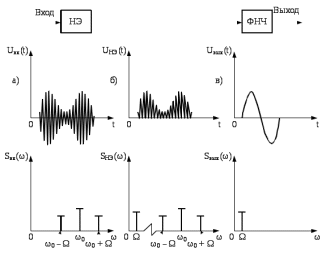
Рис. 7.6 – Спектральные и временные характеристики напряжений, поясняющих работу детектора;
а) на входе детектора
б) на выходе нелинейного элемента;
в) на выходе детектора
На рисунке 7.7 приведена принципиальная схема детектора, включающая в себя диод в качестве нелинейного элемента и RфCф– фильтр, выполняющий роль фильтра нижних частот. При выборе элементов фильтра надо выполнять условие:
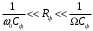
Кроме колебаний частоты Ω, на выходе нелинейного элемента могут появиться комбинационные колебания более высоких частот 2Ω; 3Ω и так далее. Эти гармоники тоже выделяются фильтром. Поэтому задача уменьшения вредных продуктов преобразования должна решаться путем выбора преобразователя с необходимыми характеристиками.
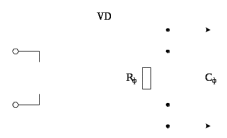
Рис. 7.7 - Схема детектора АМ-сигнала
Не трудно убедиться, что процесс детектирования, это выполнение операции: Ω = ω0 – (ω0 – Ω), 2Ω = 2ω0 – 2(ω0 – Ω) . . . Что это значит? А это говорит о том, что без несущей ω0 невозможно производить детектирование АМ-сигнала. Знание (ω0 – Ω) или (ω0 + Ω) недостаточно. Таким образом, если нет несущей, то её надо восстановить на приемной стороне.
Рис. 7.8 – Характеристика детектирования АМ-сигнала
На рисунке 7.8 показана характеристика детектирования АМ-сигнала, при этом указаны две области детектирования, 1 обл. – квадратичное детектирование, 2 обл. – линейное детектирование.
Характеристикой детектирования называется зависимость постоянной составляющей тока нелинейного элемента (нулевой гармоники) от амплитуды входного сигнала:
I0 = f(UΩ).
Рассмотрим линейное детектирование, пользуясь методом трех плоскостей, приведенных на рисунке 7.9 [5].
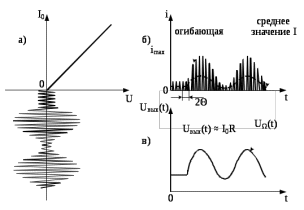
Рис.7.9 – Линейное детектирование АМ-сигнала, а) входной сигнал на входе детектора, б) сигнал на выходе диода при угле отсечки Θ=90о, в) сигнал на выходе детектора
Полезной составляющей детектора является ток нулевой гармоники, при этом угол отсечки выбирается Θ=90о , чтобы ток на выходе детектора зависел только от амплитуды входного сигнала, а это возможно если коэффициент Берга является постоянной величиной и равен α(Θ) = 1/π. Ток нулевой гармоники:
.
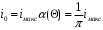Рассмотрим случай детектирования, когда нелинейный элемент аппроксимируется квадратической зависимостью: i = a2U2 .
При подаче на вход АМ-сигнала:
U(t) = Uω [1 + m cos Ωt ] cos ω0t,
На выходе диода
=
.
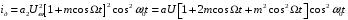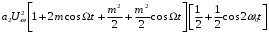Как видно из приведенного выше выражения, на выходе диода появилась вторая гармоника модулирующего сигнала, которой не было на передаче, при этом коэффициент нелинейных искажений: kн.и. = m/4.
При m = 100% kн.и = 25% а это очень большие нелинейные искажения, в том время как реально работающей аппаратуре допускается только доли процента.
7.2 Устройства формирования и детектирования сигналов с частотной модуляцией
7.2.1 Модулятор ЧМ- сигналов
Рассмотрим схемы частотной модуляции. Задачу получения ЧМ колебаний можно сформулировать как задачу создания генератора гармонических колебаний, частота которого изменяется в соответствии с изменением амплитуды модулирующего сигнала. Частота колебаний LС-генератора определяется резонансной частотой колебательного контура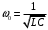
и, следовательно, для её изменения необходимо менять либо емкость С, либо индуктивность L. Для изменения частоты колебаний RC - генератора следует менять либо емкость С, либо R.
Рис.7.10 – Принципиальная схема получения ЧМ-сигнала на варикапе
На рисунке 7.10 приведена схема модулятора ЧМ-сигнала, где управляющей емкостью служит варикап [5]. Низкочастотный сигнал подается через трансформатор и дроссель на контур. Дроссель Lдрслужит для пропускания постоянной составляющей и позволяет производить шунтирование контура низкоомным сопротивлением цепи модулятора.
Частота генератора:
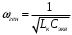Сэкв. = Cк + С0 + ΔС,
где С0 – емкость варикапа в рабочей точке при отсутствии модуляции, ΔС – изменение емкости при подаче на варикап модулирующего сигнала. Изменение емкости: С(t) = ΔС cosΩt, частота контура:
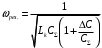
где СΣ = Ск + С0– емкость контура при отсутствии модулирующего сигнала.
К недостаткам рассматриваемого модулятора следует отнести:
- невысокая девиация частоты из-за малого линейного участка C(U), Δω ≈ ΔC;
- исключается возможность стабилизация частоты с помощью кварца.
Для увеличения девиации частоты применяется умножение частоты после модуляции, тогда Δωвых = Δωгенn, где n - коэффициент умножения.
7.2.2 Детектирование ЧМ – сигнала
Разница в приеме ЧМ и АМ колебаний состоит в методах их детектирования. Методы детектирования ЧМ колебаний можно разделить на косвенные и прямые.
Детектирование по косвенным методам осуществляется в результате одного из трех преобразований. Согласно первому преобразованию ЧМ колебание предварительно превращается в АМ колебание и затем детектируется амплитудным детектором. При втором – ЧМ колебание преобразуется в фазомодулированное (ФМ) колебание и для детектирования используется фазовый детектор. В третьем случае ЧМ колебание превращается в импульсно-модулированное колебание и затем детектируется импульсным детектором. Рассмотрим детектирование по первому способу.
Преобразование ЧМ колебание в АМ можно осуществить , например, при помощи так называемой схемы с расстроенным контуром. Допустим, что контур настроен относительно центральной частоты входного сигнала, как показано на рисунке 7.11.
Аппроксимируем участок левой резонансной кривой выражением:
y = y0 + kω.
Допустим, что частота изменяется по закону:
Ω = ω + Δω cosΩt,
следовательно, y = y0 + kω0 + kΔωcos Ωt.
Выполнив несложные преобразования
y = (y0 + kω0)[1 + (kΔω/y0 + kω0) cosΩt]
и обозначив
y + kω0 = yΣ, kΔω/y0 + kω0 = m
подставим в верхнее выражение, получим:
y = y (1 + mcosΩt)
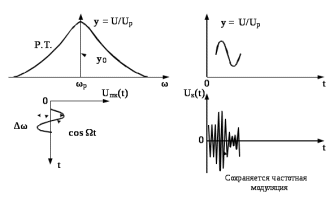
Рис.7.11 – К пояснению преобразования ЧМ – колебания в АМ - колебание
Таким образом, напряжение на выходе контура представляет собой АМ-сигнал, огибающая которого показана на рисунке 7.11 справа.
Принцип работы детектора на одном расстроенном контуре показан на рисунке 7.12.
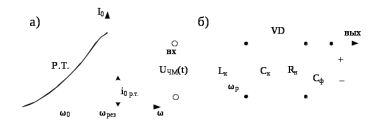
Рис.7.12 – Характеристика детектирования (а) и принципиальная схема на одном расстроенном контуре (б).
К недостаткам схемы на одном расстроенном контуре следует отнести малый линейный участок характеристики детектирования, который ограничивает девиацию частоты Δω, а также наличие постоянной составляющей тока при отсутствии модуляции.
На рисунке 7.13 приведена принципиальная схема с двумя расстроенными контурами, которая позволяет устранить недостатки схемы с одним расстроенным контуром.
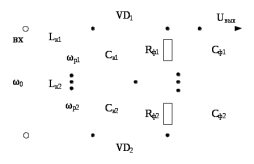
Рис. 7.13 – Принципиальная схема ЧМ детектора на двух взаимно-расстроенных контурах.
Катушки индуктивности Lk1иLk2намотаны в встречном направлении, чтобы характеристика детектирования получилась такая, как показана на рисунке 7.14.
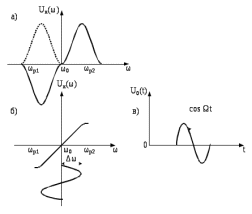
Рис.7.14 – К пояснению работы детектора ЧМ на двух взаимно расстроенных контурах, а) АЧХ расстроенных контуров, б) характеристика детектирования, в) напряжение на выходе детектора
Как видно из рисунка 7.14, допустимая девиация в два раза выше из-за расширения линейного участка детектирования, а также наличие нулевого напряжения на выходе при отсутствии сигнала.
Превышение девиации Δω допустимого значения Δωдоп приводит к нелинейным искажениям, как показано на рисунке 7.15.
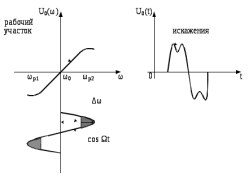
Рис. 7.15 – Превышение Δω линейного участка характеристики детектировании.
7.3 Контрольные вопросы и задачи
7.3.1 Какие требования, предъявляются к нелинейному элементу, представленному как L(x) = a0 + a1x + a2x2 + . . .akxk, который используется в модуляторе АМ – сигнала.
7.3.2 Какая часть нелинейного полиномаL(x) = a0 + a1x + a2x2 + . . .akxk используется в АМ модуляторе?
7.3.3 Записать выражение суммарного сигнала, который подается на вход АМ модулятора и обосновать необходимость каждого компонента.
7.3.4 Рассчитать статическую модуляционную характеристику для случая аппроксимации транзистора полиномом третей степени, для которой она определяется выражением:
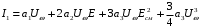
приняв Uω = 4 B, а1 = 3020 mA/B, a2 = 20 mA/B, a3 = 10 mA/B
7.3.5 Используя данные задачи 7.3.4 определить максимальное значение коэффициента неискаженной модуляции АМ сигнала.
7.3.6 При каких значения коэффициентов полиномаL(x) = a0 + a1x + a2x2 + . . .akxk, глубина (коэффициент) модуляции будет максимальной?
7.3.7 Построить спектр и временные диаграммы АМ-сигнала, (модуляция одним тоном) при изменении рабочей точки на статической модуляционной характеристике вверх и вниз.
SΩ (t) = KA(t).
Рис.7.5 – Диаграммы сигналов на входе SАМ (t) и выходеSΩ (t) детектора: а) временные; б) спектральные
На рисунке 7.6 приведена структурная схема детектора, состоящая из нелинейного элемента и фильтра нижних частот. Временные и спектральные диаграммы напряжений на рисунке подчеркивают тот факт, что модулирующего сигнала в спектре АМ-сигнала нет, и задача нелинейного элемента, именно его выделить из АМ-сигнала.
Рис. 7.6 – Спектральные и временные характеристики напряжений, поясняющих работу детектора;
а) на входе детектора
б) на выходе нелинейного элемента;
в) на выходе детектора
На рисунке 7.7 приведена принципиальная схема детектора, включающая в себя диод в качестве нелинейного элемента и RфCф– фильтр, выполняющий роль фильтра нижних частот. При выборе элементов фильтра надо выполнять условие:
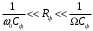
Кроме колебаний частоты Ω, на выходе нелинейного элемента могут появиться комбинационные колебания более высоких частот 2Ω; 3Ω и так далее. Эти гармоники тоже выделяются фильтром. Поэтому задача уменьшения вредных продуктов преобразования должна решаться путем выбора преобразователя с необходимыми характеристиками.
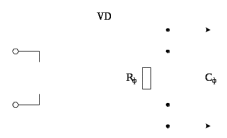
Рис. 7.7 - Схема детектора АМ-сигнала
Не трудно убедиться, что процесс детектирования, это выполнение операции: Ω = ω0 – (ω0 – Ω), 2Ω = 2ω0 – 2(ω0 – Ω) . . . Что это значит? А это говорит о том, что без несущей ω0 невозможно производить детектирование АМ-сигнала. Знание (ω0 – Ω) или (ω0 + Ω) недостаточно. Таким образом, если нет несущей, то её надо восстановить на приемной стороне.
Рис. 7.8 – Характеристика детектирования АМ-сигнала
На рисунке 7.8 показана характеристика детектирования АМ-сигнала, при этом указаны две области детектирования, 1 обл. – квадратичное детектирование, 2 обл. – линейное детектирование.
Характеристикой детектирования называется зависимость постоянной составляющей тока нелинейного элемента (нулевой гармоники) от амплитуды входного сигнала:
I0 = f(UΩ).
Рассмотрим линейное детектирование, пользуясь методом трех плоскостей, приведенных на рисунке 7.9 [5].
Рис.7.9 – Линейное детектирование АМ-сигнала, а) входной сигнал на входе детектора, б) сигнал на выходе диода при угле отсечки Θ=90о, в) сигнал на выходе детектора
Полезной составляющей детектора является ток нулевой гармоники, при этом угол отсечки выбирается Θ=90о , чтобы ток на выходе детектора зависел только от амплитуды входного сигнала, а это возможно если коэффициент Берга является постоянной величиной и равен α(Θ) = 1/π. Ток нулевой гармоники:
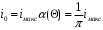.Рассмотрим случай детектирования, когда нелинейный элемент аппроксимируется квадратической зависимостью: i = a2U2 .
При подаче на вход АМ-сигнала:
U(t) = Uω [1 + m cos Ωt ] cos ω0t,
На выходе диода
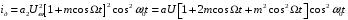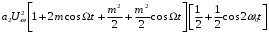= .Как видно из приведенного выше выражения, на выходе диода появилась вторая гармоника модулирующего сигнала, которой не было на передаче, при этом коэффициент нелинейных искажений: kн.и. = m/4.
При m = 100% kн.и = 25% а это очень большие нелинейные искажения, в том время как реально работающей аппаратуре допускается только доли процента.
7.2 Устройства формирования и детектирования сигналов с частотной модуляцией
7.2.1 Модулятор ЧМ- сигналов
Рассмотрим схемы частотной модуляции. Задачу получения ЧМ колебаний можно сформулировать как задачу создания генератора гармонических колебаний, частота которого изменяется в соответствии с изменением амплитуды модулирующего сигнала. Частота колебаний LС-генератора определяется резонансной частотой колебательного контура
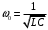и, следовательно, для её изменения необходимо менять либо емкость С, либо индуктивность L. Для изменения частоты колебаний RC - генератора следует менять либо емкость С, либо R. Рис.7.10 – Принципиальная схема получения ЧМ-сигнала на варикапе
На рисунке 7.10 приведена схема модулятора ЧМ-сигнала, где управляющей емкостью служит варикап [5]. Низкочастотный сигнал подается через трансформатор и дроссель на контур. Дроссель Lдрслужит для пропускания постоянной составляющей и позволяет производить шунтирование контура низкоомным сопротивлением цепи модулятора.
Частота генератора:
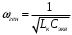Сэкв. = Cк + С0 + ΔС,где С0 – емкость варикапа в рабочей точке при отсутствии модуляции, ΔС – изменение емкости при подаче на варикап модулирующего сигнала. Изменение емкости: С(t) = ΔС cosΩt, частота контура:
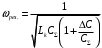
где СΣ = Ск + С0– емкость контура при отсутствии модулирующего сигнала.
К недостаткам рассматриваемого модулятора следует отнести:
- невысокая девиация частоты из-за малого линейного участка C(U), Δω ≈ ΔC;
- исключается возможность стабилизация частоты с помощью кварца.
Для увеличения девиации частоты применяется умножение частоты после модуляции, тогда Δωвых = Δωгенn, где n - коэффициент умножения.
7.2.2 Детектирование ЧМ – сигнала
Разница в приеме ЧМ и АМ колебаний состоит в методах их детектирования. Методы детектирования ЧМ колебаний можно разделить на косвенные и прямые.
Детектирование по косвенным методам осуществляется в результате одного из трех преобразований. Согласно первому преобразованию ЧМ колебание предварительно превращается в АМ колебание и затем детектируется амплитудным детектором. При втором – ЧМ колебание преобразуется в фазомодулированное (ФМ) колебание и для детектирования используется фазовый детектор. В третьем случае ЧМ колебание превращается в импульсно-модулированное колебание и затем детектируется импульсным детектором. Рассмотрим детектирование по первому способу.
Преобразование ЧМ колебание в АМ можно осуществить , например, при помощи так называемой схемы с расстроенным контуром. Допустим, что контур настроен относительно центральной частоты входного сигнала, как показано на рисунке 7.11.
Аппроксимируем участок левой резонансной кривой выражением:
y = y0 + kω.
Допустим, что частота изменяется по закону:
Ω = ω + Δω cosΩt,
следовательно, y = y0 + kω0 + kΔωcos Ωt.
Выполнив несложные преобразования
y = (y0 + kω0)[1 + (kΔω/y0 + kω0) cosΩt]
и обозначив
y + kω0 = yΣ, kΔω/y0 + kω0 = m
подставим в верхнее выражение, получим:
y = y (1 + mcosΩt)
Рис.7.11 – К пояснению преобразования ЧМ – колебания в АМ - колебание
Таким образом, напряжение на выходе контура представляет собой АМ-сигнал, огибающая которого показана на рисунке 7.11 справа.
Принцип работы детектора на одном расстроенном контуре показан на рисунке 7.12.
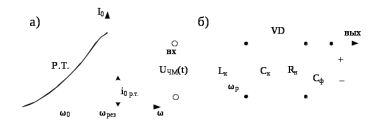
Рис.7.12 – Характеристика детектирования (а) и принципиальная схема на одном расстроенном контуре (б).
К недостаткам схемы на одном расстроенном контуре следует отнести малый линейный участок характеристики детектирования, который ограничивает девиацию частоты Δω, а также наличие постоянной составляющей тока при отсутствии модуляции.
На рисунке 7.13 приведена принципиальная схема с двумя расстроенными контурами, которая позволяет устранить недостатки схемы с одним расстроенным контуром.
Рис. 7.13 – Принципиальная схема ЧМ детектора на двух взаимно-расстроенных контурах.
Катушки индуктивности Lk1иLk2намотаны в встречном направлении, чтобы характеристика детектирования получилась такая, как показана на рисунке 7.14.
Рис.7.14 – К пояснению работы детектора ЧМ на двух взаимно расстроенных контурах, а) АЧХ расстроенных контуров, б) характеристика детектирования, в) напряжение на выходе детектора
Как видно из рисунка 7.14, допустимая девиация в два раза выше из-за расширения линейного участка детектирования, а также наличие нулевого напряжения на выходе при отсутствии сигнала.
Превышение девиации Δω допустимого значения Δωдоп приводит к нелинейным искажениям, как показано на рисунке 7.15.
Рис. 7.15 – Превышение Δω линейного участка характеристики детектировании.
7.3 Контрольные вопросы и задачи
7.3.1 Какие требования, предъявляются к нелинейному элементу, представленному как L(x) = a0 + a1x + a2x2 + . . .akxk, который используется в модуляторе АМ – сигнала.
7.3.2 Какая часть нелинейного полиномаL(x) = a0 + a1x + a2x2 + . . .akxk используется в АМ модуляторе?
7.3.3 Записать выражение суммарного сигнала, который подается на вход АМ модулятора и обосновать необходимость каждого компонента.
7.3.4 Рассчитать статическую модуляционную характеристику для случая аппроксимации транзистора полиномом третей степени, для которой она определяется выражением:
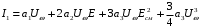
приняв Uω = 4 B, а1 = 3020 mA/B, a2 = 20 mA/B, a3 = 10 mA/B
7.3.5 Используя данные задачи 7.3.4 определить максимальное значение коэффициента неискаженной модуляции АМ сигнала.
7.3.6 При каких значения коэффициентов полиномаL(x) = a0 + a1x + a2x2 + . . .akxk, глубина (коэффициент) модуляции будет максимальной?
7.3.7 Построить спектр и временные диаграммы АМ-сигнала, (модуляция одним тоном) при изменении рабочей точки на статической модуляционной характеристике вверх и вниз.