ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 261
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
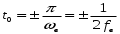
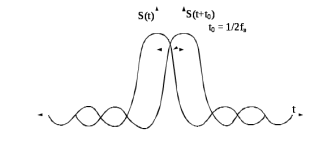
Рис. 2.5 – Временные зависимости ортогональных функций, сдвинутых во времени
Из рассмотренного выше следует путь построения бесконечного ортогонального базиса, который может служить координатной системой для разложения произвольного сигнала со спектром, ограниченным частотой ωв.
- 1 2 3 4 5 6 7 8 9 10
Теорема Котельникова
В свою время В. А. Котельников доказал теорему, которая является одним из фундаментальных положений теоретической радиотехники. Эта теорема устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром исходя из отчетных значений, взятых через равные промежутки времени.
Теорема Котельникова: любая непрерывная функция, спектр которой не содержит частот выше ωв, полностью определяется своими отсчетами, взятыми через интервал времени: Δt =π/ωв=1/2fв .
На рисунке 2.6 приведен пример дискретизации непрерывного аналогового сигнала.
Рис.2.6 – Образование дискретного сигнала S(kΔt) после операции дискретизации S(t)
Как правило, спектр реального сигнала бесконечен, поэтому необходимо ограничить полосу частот с помощью фильтра (рисунок 2.7)
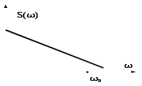
Рис.2.7 – Идеальное ограничение спектра непрерывного сигнала
При идеальном ограничении спектра непрерывного сигнала, спектр после операции дискретизации представлен на рисунке 2.8, где график спектра построен при использовании интервала Котельникова Δt =π/ωв=1/2fв .
В настоящее время для ограничения спектра исходного сигнала используется цифровая фильтрация, которая позволяет получить резкий спад передаточной функции фильтра, так как при аналоговой фильтрации этого получить не удается.
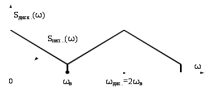
Рис.2.8 – Спектр сигнала после операции дискретизации по теореме Котельникова
На рисунке 2.8 изображена только часть спектра дискретизированного сигнала, до частоты 2ωв+ ωв, который будет рассмотрен в дальнейшем. Полный спектр дискретизированного сигнала будет включать в себя боковые составляющие исходного непрерывного сигнала относительно центральной частоты 2 ωдис,
3ωдис, 4 ωдис . . . . n ωдис.. Как следует из рисунка, информация об исходном сигнале лежит в диапазоне частот от 0 до ωв. Таким образом, устройством, который выделит непрерывный сигнал, будет фильтр нижних частот (ФНЧ).
Для восстановления исходного сигнала необходимо воспользоваться рядом Котельникова:
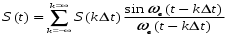(2.5)где S(t) – восстановленный сигнал, S(kΔt) - отсчеты сигнала, которые получены при дискретизации с интервалом Котельникова, равного Δt=1/2fв,
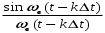- импульсная реакция идеализированного низкочастотного фильтра, другими словами, набор ортогональных функций, показанных на рисунке 2.5.В отличие от идеализированного фильтра нижних частот, реальный фильтр имеет АЧХ и ФЧХ, значительно отличающееся от идеального фильтра, а именно, неравномерную АЧХ в полосе пропускания и нелинейную ФЧХ. Неравномерная ФЧХ отличается различным временем запаздывания гармоник сигнала.
На рисунке 2.9 показан процесс восстановления исходного непрерывного сигнала по отсчетам Котельникова [5].
Рис. 2.9 – Процесс восстановления сигнала по отсчетам Котельникова
S(kΔt)
2.3 Погрешности дискретизации и восстановления непрерывных
сигналов
Теорема Котельникова справедлива только для сигналов с ограниченным спектром. Однако спектры реальных сигналов бесконечны, так как они, как правило, существуют на ограниченном промежутке времени. В этом случае теорема Котельника справедлива с погрешностью. Погрешность ΔEп в соответствии с рисунком 2.10 можно определить как:
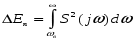
Рис.2.10 – Спектр сигнала, ограниченного частотой ωв
Вторая причина возникновения погрешностей - неидеальность АЧХ и ФЧХ восстанавливающего ФНЧ. Происходит изменение импульсной реакции ФНЧ по оси времени, смещение sinx/x.
С другой стороны, следует учитывать результат ограничения спектра сигнала до операции дискретизации и наличие помех в области от ωв до ωД (рисунок 2.11). При использовании аналогового фильтра не удается убрать частоты спектра превышающие ωв и часть помех.
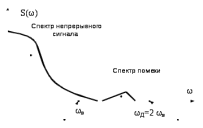
Рис.2.11 – Спектр сигнала до операции дискретизации при применении аналогового фильтра
Как показано на рисунке 2.12, в условиях, описанных выше, и при частоте дискретизации согласно теоремы Котельникова, спектр отсчетов непрерывного сигнала в области от 0 до ωв включает в себя и помеху, и спектр не полностью отфильтрованного сигнала (искажения).
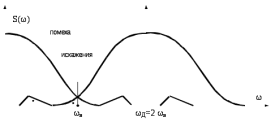
Рис. 2.12 – Спектр дискретизированного непрерывного сигнала согласно теореме Котельникова
В современных цифровых системах для устранения помех и искажений используется дискретизация на частоте в 3 – 5 раз выше 2 ωв. Получаемый при этом сигнал, фильтруется цифровых фильтров, а затем считывается с необходимой частотой.
2.4 Контрольные вопросы и задачи
2.4.1 Каким образом можно качественно оценить и сравнить между собой требуемую частоту дискретизации по временным диаграммам двух различных сигналов, подлежащих амплитудно-импульсному преобразованию на примере рисунка 2.13.
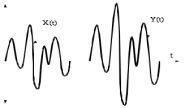
Рис.2.13 – Пример двух сигналов для операции дискретизации
2.4.2 На примере математического выражения ряда Котельникова необходимо дать пояснение компонентам, входящих в формулу (2.5).
2.4.3 Какую форму приобретет спектр сигнала на выходе модулятора, если на вход будет подан сигнал вида (рисунок 2.14), при этом отсчеты берутся как в соответствии с теоремой Котельникова, так и в 2 раза чаще. Рассмотреть для разных максимальных значений частоты спектра.
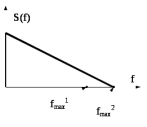
Рис.2.14 – Спектр исходного сигнала с разными вариантами определения максимальной частоты спектра
2.4.4 Объяснить принцип восстановления сигнала с ограниченным спектром по отсчетам Котельникова с помощью идеального фильтра нижних частот.
2.4.5
С какой целью ограничивают ширину спектра непрерывного сигнала, передаваемого по каналу связи отсчетами Котельникова?
2.4.6 Приведите математическое выражение и графики амплитудно-частотной и фазо-частотной характеристик идеального ФНЧ.
2.4.7 Выберите частоту дискретизации для импульсной передачи сигнала тональной частоты со спектром 0,3 – 3,4 кГц.
2.4.8 Приведите выражение, описывающее импульсную характеристику идеального ФНЧ и изобразите график.
2.4.9 На вход амплитудно-импульсного модулятора с частотой дискретизации fдиск. = 200 кГц подается непрерывный сигнал. Какой может быть максимальная частота в спектре этого сигнала, чтобы амплитудно-импульсной преобразование осуществлялась без помех
2.4.10 Пояснить особенности характеристик реальных фильтров нижних частот по сравнению с характеристиками идеального ФНЧ.
2.4.11 Графически изобразите случай, когда отсчеты берутся недостаточно часто для того, чтобы можно было воспользоваться рядом Котельникова для точного отображения сигнала.
2.4.12 Объясните причины погрешности восстановления реальных сигналов.
2.4.13 Изобразите графики нескольких функций, принадлежащих базису Котельникова. Перечислите их характерные свойства.
2.4.14 Какая взаимосвязь между импульсной характеристикой фильтра и его комплексным коэффициентом передачи на основе преобразования Фурье.
2.4.15. Синусоидальный (гармонический) сигнал с частотой f = 2кГц дискретизируется с частотой fдиск. = 10кГц. Нарисовать временную и спектральную диаграмму сигнала на выходе модулятора.
2.4.16 Запишите формулу ряда Котельникова и сформулируйте соответствующую теорему.
2.4.17 Изобразите спектральную диаграмму сигнала на выходе модулятора для случая, когда отсчеты сигнала с ограниченным спектром берутся в 2 раза чаще, чем это необходимо по теореме Котельникова.
3 Модулированные аналоговые сигналы
3.1 Сигналы с амплитудной модуляцией.
Сигналы, поступающие из источника сообщений (микрофон, телевизионная камера, датчик телеметрической информации), как правило, не могут быть непосредственно переданы по радиоканалу. Дело не только в том, что эти сигналы недостаточно велики по амплитуде. Гораздо существеннее их относительная низкочастотность, да еще полоса частот часто совпадает, что мешает их уплотнению по каналу. Для осуществления эффективной передачи в какой-то среде, необходимо перенести спектр этих сигналов из низкочастотной области в область достаточно высоких частот. Кроме того, для уплотнения канала связи, увеличению количества абонентов, тоже требуется перенос спектра исходного низкочастотного сигнала в область высоких частот. Данная процедура получила в радиотехнике название