ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 257
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(1.8)
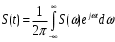
В итоге мы получаем: спектральное представление сигнала открывает прямой путь к анализу прохождения сигнала через широкий класс радиотехнических, устройств, а также сложных систем.
Определить спектральную плотность прямоугольного видеоимпульса.
Пусть сигнал S(t) имеет амплитуду U, длительность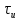
и располагается симметрично относительно начала отсчета времени.
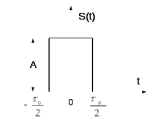
Рис. 1.6 - Симметричный сигнал прямоугольной формы
В соответствии с (1.6):
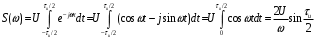
Таким образом, спектральная плотность рассматриваемого сигнала есть вещественная функция частоты. Введем безразмерную переменную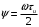
и представим результат как:
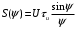(1.9)
Отметим, что значение спектральной плотности на нулевой частоте равно площади импульса: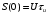
.
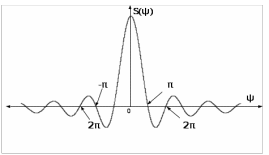
Рис.1.7 - График нормированной спектральной плотности прямоугольного видеоимпульса как функция параметра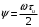
График, построенный по формуле (1.9) представлен на рис.1.7
Рассмотрим сигнал, описываемый функцией экспоненциальной зависимостью S(t) = Uexp(βt), при положительном значении β (рис.1.8)
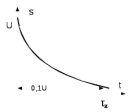
Рис. 1.8 - Экспоненциальный сигнал
Сигнал, представленный на рис.1.8 лишь условно можно называть импульсом из-за
. Однако, условие β > 0 обеспечивает быстрое уменьшение мгновенных значений сигнала с ростом времени. Эффективную длительность подобных импульсов в радиотехнике обычно определяют из условия десятикратного уменьшения уровня сигнала: exp(-βτи ) = 0,1 , откуда τи = 2,303/β.
Спектральная плотность экспоненциального видеоимпульса:
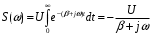
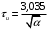
Особенностью спектральной плотности экспоненциального сигнала от спектра импульса прямоугольной формы является то, что что величина S(ω) не обращается в нуль и представляется как комплекснозначная функция:
S(ω) = |S(ω)| exp[jψ(ω)],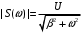
, ψ(ω) =-arctg(ω/β).
Импульс с гауссовской огибающей описывается функцией:
S(t) = Uexp(-αt2).
Эффективная длительность гауссова импульса определяется из условия десятикратного уменьшения мгновенного значения сигнала, при этом длительность должна удовлетворять соотношению exp[-α(τи/)2] = 0,1, что позволяет получить:
Опуская дальнейшие выкладки и ссылаясь на [1], получим выражение спектральной плотности гауссова импульса:
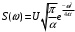
Спектральную плотность дельта-функции, представленная как существование сигнала S(t) = Aδ(t) только в точке t = 0 и имеющая площадь А, можно представить как:S(ω) = A = const.
Таким образом, дельта-импульс имеет равномерный спектр на всех частотах.
Главный вывод из спектрального анализа сигналов, приведенных выше, это: чем меньше длительность импульса, тем шире его спектр.
Под шириной импульса будем понимать частотный интервал, в пределах которого, модуль спектральной плотности не меньше некоторого наперед заданного уровня, например, изменяется в пределах от |S|max до 0,1|S|max .
Рассмотрим прямоугольный видеоимпульс, полагая при этом, что верхняя граничная частота – это частота, соответствующая первому нулю спектральной плотности. Видно, что
Ωв τи/2 = π или fвτи = 1.
Для экспоненциального видеоимпульса, уменьшение в 10 раз по отношению в максимальному значению [1]:
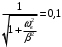или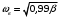 
, а значит fв = ωи/(2π) = 1,584
.
Итак, произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса и, как правило, имеющее порядок единицы:
fвτи =
const.
Это соотношение имеет первостепенное значение для радиотехники. Оно определяет требования к ширине полосы пропускания радиотехнических устройств.
1.3 Контрольные вопросы и задачи
1.3.1 Почему простое гармоническое колебание cos (ω0t + φ0) играет особо важную роль в радиотехнике?
1.3.2 Дайте определение понятия периодического сигнала. Назовите несколько физических процессов, для которых модель периодического сигнала является достаточно точным способом описания.
1.3.3 Какова связь между длительностью импульса и шириной его спектра?
1.3.4 Каким образом можно проверить ортогональность сигналов?
1.3.5 Определить амплитудный и фазовый спектр для последовательности прямоугольных импульсов (рисунок 1.9) при скважности равной 2, амплитуды импульса А = 1В, Х = 0.
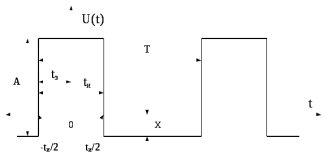
Рис.1.9 –Последовательность прямоугольных импульсов четного характера
1.3.6 Определить фазовый спектр для сигнала (рисунок 1.9) для скважности, равной 3 и первых 4 гармоник для tз = 0 и tзсогласно рисунку.
1.3.7 От каких параметров импульсного сигнала зависит амплитудный спектр, начиная с первой гармоники и далее.
1.3.8 На рисунке 1.10 приведен пример импульсной последовательности нечетного характера. Рассчитать фазовый спектр для первых четырех гармоник, если скважность равна 3.
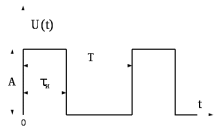
Рис.1.10 - Последовательность прямоугольных импульсов нечетного характера
1.3.9 Показать, что импульсные последовательности на рисунке 1.9 и 1.10 имеют одинаковый амплитудный спектр при равных амплитудах и скважностях
1.3.10 Показать, что набор ортогональных функций Фурье попарно ортогональны.
1.3.11 При каком соотношении частот сигналы:
S1 (t) = Acosω1t и S2 (t) = Acosω2t ортогональны на интервале Т.
2 Сигналы с ограниченным спектром
2.1 Модели сигналов с ограниченным спектром
Для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, лежащими в интервале от нуля до бесконечности. Однако физически такая процедура принципиально неосуществима. К тому же, вклад спектральных составляющих при условии
ω→∞ пренебрежимо мал в силу ограниченности энергии сигналов. При этом, любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.
Поэтому целесообразно представлять математическую модель сигнала, которое имеет такое свойство: спектральная плотность колебания отлична от нуля лишь в пределах некоторой полосы частот конечной протяженности. В радиотехнике подобный сигнал называют сигналом с ограниченным спектром.
Математическую модель сигнала с ограниченным спектром во временной области можно получить из формулы обратного преобразования Фурье:
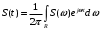
В зависимости от выбора отрезка R и функции S(ω) можно получить разнообразные виды сигналов с ограниченным спектром.
Рассмотрим идеальный низкочастотный сигнал. Представим колебание с постоянной вещественной спектральной плотностью в пределах отрезка частот от нуля до верхней граничной частоты ω0. Вне этого отрезка спектральная плотность сигнала обращается в нуль:
S(ω) = S0, если -ωв ≤ ω ≤ ωв и 0 при других значениях ω (2.1)
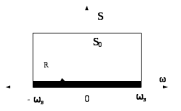
Рис.2.1 – Спектр идеального низкочастотного сигнала
Мгновенное значение такого сигнала
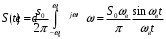(2.2)
В дальнейшем будем называть такое колебание идеальным низкочастотным сигналом, подчеркивая этим простейший вид его спектра по сравнению со спектром других возможных сигналов подобного вида.
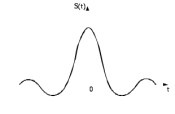
Рис.2.2 – Временная характеристика идеального низкочастотного сигнала
Идеальный низкочастотный сигнал более общего вида получается, если в формулу (2.1) ввести фазу спектральной плотности, линейно зависящей от частоты:
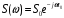, если -ωв ≤ ω ≤ ωв и 0 при других значениях ω (2.3)
Спектральной плотности (2.3) соответствует низкочастотный сигнал
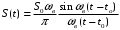(2.4)
Смещенный во времени относительно сигнала (2.2) на t0секунд.
Идеальный низкочастотный сигнал является идеализированной выходной реакцией фильтра частот (ФНЧ), возбуждаемого колебанием с равномерной по частоте спектральной плотностью, то есть дельта импульсом.
Рассмотрим математическую модель сигнала, спектр которого ограничен полосами частот шириной 2Δω, каждая с центром на частоте ± ω0. Если в пределах этих полос, спектральная плотность сигнала постоянна, то данный сигнал будем называть идеальным полосовым сигналом.
Мгновенные значения этого сигнала найдем, используя обратное преобразование Фурье:
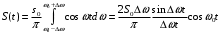(2.5)
При построении графика, мы видим, что наряду с высокочастотными осцилляциями на частоте ω0 наблюдается изменение во времени мгновенного значения их амплитуд. Функция sin(Δωt)/Δωt с точностью до масштабного коэффициента 2S0Δω/π играет роль медленной огибающей идеального полосового сигнала.
Теоретически возможный способ получения идеального полосового сигнала очевиден: на вход идеального полосового фильтра, пропускающего лишь колебания с частотами в пределах полосы [ω0 -Δω, ω0 +Δω] , должно быть подано широкополосное воздействие вида дельта-функции.
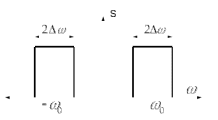
Рис. 2.3 – Спектр идеального полосового сигнала
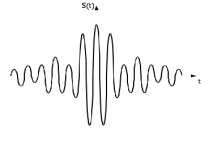
Рис.2.4 – Временная характеристика идеального полосового сигнала
Свойство ограниченности спектра позволяет находить интересные и важные классы ортогональных сигналов. Простейший пример – два ортогональных полосовых сигналов, области которых не пересекаются. Равенство нулю скалярного произведения этих сигналов непосредственно следует из обобщенной формулы Рэлея [1].
Другой очевидный способ ортогонализации сигналов с ограниченным спектром заключается в их временном сдвиге. Рассмотрим два идеальных низкочастотных сигналов u(t) и v(t), при этом сигнал u(t) запаздывает по отношению к сигналу v(t) на время t0, так что его спектральная плотность V(ω) = U(ω)exp(-jωt0).
Скалярное произведение этих сигналов, вычисленное через спектральные плотности:
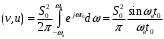
Скалярное произведение обращается в нуль, и два одинаковых по форме идеальных низкочастотных сигналов оказывается ортогональными, если:
.
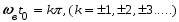Минимально возможный сдвиг, приводящий к ортогонализации, получается при k=1 или -1, это соответствует:
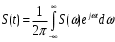
В итоге мы получаем: спектральное представление сигнала открывает прямой путь к анализу прохождения сигнала через широкий класс радиотехнических, устройств, а также сложных систем.
Определить спектральную плотность прямоугольного видеоимпульса.
Пусть сигнал S(t) имеет амплитуду U, длительность
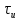и располагается симметрично относительно начала отсчета времени.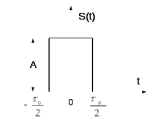 Рис. 1.6 - Симметричный сигнал прямоугольной формы
В соответствии с (1.6):
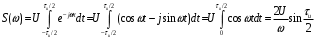
Таким образом, спектральная плотность рассматриваемого сигнала есть вещественная функция частоты. Введем безразмерную переменную
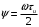и представим результат как: 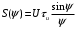(1.9)Отметим, что значение спектральной плотности на нулевой частоте равно площади импульса:
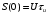. Рис.1.7 - График нормированной спектральной плотности прямоугольного видеоимпульса как функция параметра
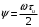
График, построенный по формуле (1.9) представлен на рис.1.7
Рассмотрим сигнал, описываемый функцией экспоненциальной зависимостью S(t) = Uexp(βt), при положительном значении β (рис.1.8)
Рис. 1.8 - Экспоненциальный сигнал
Сигнал, представленный на рис.1.8 лишь условно можно называть импульсом из-за
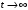. Однако, условие β > 0 обеспечивает быстрое уменьшение мгновенных значений сигнала с ростом времени. Эффективную длительность подобных импульсов в радиотехнике обычно определяют из условия десятикратного уменьшения уровня сигнала: exp(-βτи ) = 0,1 , откуда τи = 2,303/β.Спектральная плотность экспоненциального видеоимпульса:
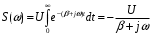
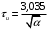
Особенностью спектральной плотности экспоненциального сигнала от спектра импульса прямоугольной формы является то, что что величина S(ω) не обращается в нуль и представляется как комплекснозначная функция:
S(ω) = |S(ω)| exp[jψ(ω)],
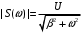, ψ(ω) =-arctg(ω/β).Импульс с гауссовской огибающей описывается функцией:
S(t) = Uexp(-αt2).
Эффективная длительность гауссова импульса определяется из условия десятикратного уменьшения мгновенного значения сигнала, при этом длительность должна удовлетворять соотношению exp[-α(τи/)2] = 0,1, что позволяет получить:
Опуская дальнейшие выкладки и ссылаясь на [1], получим выражение спектральной плотности гауссова импульса:
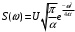
Спектральную плотность дельта-функции, представленная как существование сигнала S(t) = Aδ(t) только в точке t = 0 и имеющая площадь А, можно представить как:S(ω) = A = const.
Таким образом, дельта-импульс имеет равномерный спектр на всех частотах.
Главный вывод из спектрального анализа сигналов, приведенных выше, это: чем меньше длительность импульса, тем шире его спектр.
Под шириной импульса будем понимать частотный интервал, в пределах которого, модуль спектральной плотности не меньше некоторого наперед заданного уровня, например, изменяется в пределах от |S|max до 0,1|S|max .
Рассмотрим прямоугольный видеоимпульс, полагая при этом, что верхняя граничная частота – это частота, соответствующая первому нулю спектральной плотности. Видно, что
Ωв τи/2 = π или fвτи = 1.
Для экспоненциального видеоимпульса, уменьшение в 10 раз по отношению в максимальному значению [1]:
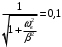или 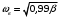, а значит fв = ωи/(2π) = 1,584 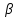.Итак, произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса и, как правило, имеющее порядок единицы:
fвτи =
const.
Это соотношение имеет первостепенное значение для радиотехники. Оно определяет требования к ширине полосы пропускания радиотехнических устройств.
1.3 Контрольные вопросы и задачи
1.3.1 Почему простое гармоническое колебание cos (ω0t + φ0) играет особо важную роль в радиотехнике?
1.3.2 Дайте определение понятия периодического сигнала. Назовите несколько физических процессов, для которых модель периодического сигнала является достаточно точным способом описания.
1.3.3 Какова связь между длительностью импульса и шириной его спектра?
1.3.4 Каким образом можно проверить ортогональность сигналов?
1.3.5 Определить амплитудный и фазовый спектр для последовательности прямоугольных импульсов (рисунок 1.9) при скважности равной 2, амплитуды импульса А = 1В, Х = 0.
Рис.1.9 –Последовательность прямоугольных импульсов четного характера
1.3.6 Определить фазовый спектр для сигнала (рисунок 1.9) для скважности, равной 3 и первых 4 гармоник для tз = 0 и tзсогласно рисунку.
1.3.7 От каких параметров импульсного сигнала зависит амплитудный спектр, начиная с первой гармоники и далее.
1.3.8 На рисунке 1.10 приведен пример импульсной последовательности нечетного характера. Рассчитать фазовый спектр для первых четырех гармоник, если скважность равна 3.
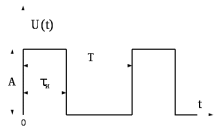
Рис.1.10 - Последовательность прямоугольных импульсов нечетного характера
1.3.9 Показать, что импульсные последовательности на рисунке 1.9 и 1.10 имеют одинаковый амплитудный спектр при равных амплитудах и скважностях
1.3.10 Показать, что набор ортогональных функций Фурье попарно ортогональны.
1.3.11 При каком соотношении частот сигналы:
S1 (t) = Acosω1t и S2 (t) = Acosω2t ортогональны на интервале Т.
2 Сигналы с ограниченным спектром
2.1 Модели сигналов с ограниченным спектром
Для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, лежащими в интервале от нуля до бесконечности. Однако физически такая процедура принципиально неосуществима. К тому же, вклад спектральных составляющих при условии
ω→∞ пренебрежимо мал в силу ограниченности энергии сигналов. При этом, любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.
Поэтому целесообразно представлять математическую модель сигнала, которое имеет такое свойство: спектральная плотность колебания отлична от нуля лишь в пределах некоторой полосы частот конечной протяженности. В радиотехнике подобный сигнал называют сигналом с ограниченным спектром.
Математическую модель сигнала с ограниченным спектром во временной области можно получить из формулы обратного преобразования Фурье:
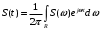
В зависимости от выбора отрезка R и функции S(ω) можно получить разнообразные виды сигналов с ограниченным спектром.
Рассмотрим идеальный низкочастотный сигнал. Представим колебание с постоянной вещественной спектральной плотностью в пределах отрезка частот от нуля до верхней граничной частоты ω0. Вне этого отрезка спектральная плотность сигнала обращается в нуль:
S(ω) = S0, если -ωв ≤ ω ≤ ωв и 0 при других значениях ω (2.1)
Рис.2.1 – Спектр идеального низкочастотного сигнала
Мгновенное значение такого сигнала
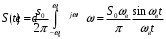(2.2)В дальнейшем будем называть такое колебание идеальным низкочастотным сигналом, подчеркивая этим простейший вид его спектра по сравнению со спектром других возможных сигналов подобного вида.
Рис.2.2 – Временная характеристика идеального низкочастотного сигнала
Идеальный низкочастотный сигнал более общего вида получается, если в формулу (2.1) ввести фазу спектральной плотности, линейно зависящей от частоты:
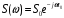, если -ωв ≤ ω ≤ ωв и 0 при других значениях ω (2.3)Спектральной плотности (2.3) соответствует низкочастотный сигнал
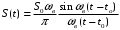(2.4)Смещенный во времени относительно сигнала (2.2) на t0секунд.
Идеальный низкочастотный сигнал является идеализированной выходной реакцией фильтра частот (ФНЧ), возбуждаемого колебанием с равномерной по частоте спектральной плотностью, то есть дельта импульсом.
Рассмотрим математическую модель сигнала, спектр которого ограничен полосами частот шириной 2Δω, каждая с центром на частоте ± ω0. Если в пределах этих полос, спектральная плотность сигнала постоянна, то данный сигнал будем называть идеальным полосовым сигналом.
Мгновенные значения этого сигнала найдем, используя обратное преобразование Фурье:
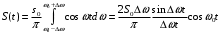(2.5) При построении графика, мы видим, что наряду с высокочастотными осцилляциями на частоте ω0 наблюдается изменение во времени мгновенного значения их амплитуд. Функция sin(Δωt)/Δωt с точностью до масштабного коэффициента 2S0Δω/π играет роль медленной огибающей идеального полосового сигнала.
Теоретически возможный способ получения идеального полосового сигнала очевиден: на вход идеального полосового фильтра, пропускающего лишь колебания с частотами в пределах полосы [ω0 -Δω, ω0 +Δω] , должно быть подано широкополосное воздействие вида дельта-функции.
Рис. 2.3 – Спектр идеального полосового сигнала
Рис.2.4 – Временная характеристика идеального полосового сигнала
Свойство ограниченности спектра позволяет находить интересные и важные классы ортогональных сигналов. Простейший пример – два ортогональных полосовых сигналов, области которых не пересекаются. Равенство нулю скалярного произведения этих сигналов непосредственно следует из обобщенной формулы Рэлея [1].
Другой очевидный способ ортогонализации сигналов с ограниченным спектром заключается в их временном сдвиге. Рассмотрим два идеальных низкочастотных сигналов u(t) и v(t), при этом сигнал u(t) запаздывает по отношению к сигналу v(t) на время t0, так что его спектральная плотность V(ω) = U(ω)exp(-jωt0).
Скалярное произведение этих сигналов, вычисленное через спектральные плотности:
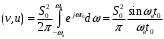
Скалярное произведение обращается в нуль, и два одинаковых по форме идеальных низкочастотных сигналов оказывается ортогональными, если:
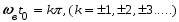.Минимально возможный сдвиг, приводящий к ортогонализации, получается при k=1 или -1, это соответствует: