, откуда сразу следует, что есть единственная пара остальных переменных, удовлетворяющих условию задачи: y = 1, z = 0, и вторая строка олжна быть копией первой (второй подходящей пары y , z нет!), что противоречит условию

6. 
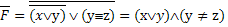
   это значит, что x – это не первый, а второй столбец:
   

   	?	x	?	F
   1	0	0		0
   2	0			0

7. 
   если при этом предположить, что первый столбец – это y, то в первой строке получаем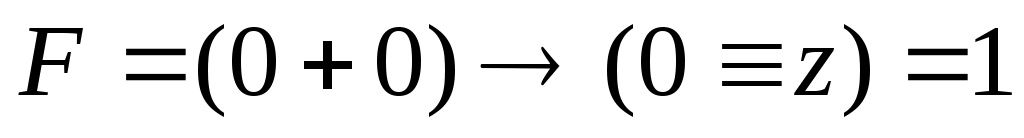 (при любом z!), что противоречит условию; поэтому первый столбец – это z, а третий – y
   
8. 
   на всякий случай проверяем первую строку: справедливо при y = 1
   
9. 
   во второй строке условие справедливо при x = 1 и y = 1 (что отличается от варианта в первой строке значением x)
   
10. 
    Ответ: zxy.
    

Решение (построение части таблицы истинности, С.В. Логинова):

1. 
   По свойству импликации функция имеет значение 0 тогда, когда в первой скобке получится 0, а во второй 1. Из этого следует что возможные сочетания для переменных x и y равны 01, 10, 11.
   
2. 
   Вторая скобка равна 0, если y и z имеют разные значения.
   
3. 
   Составим таблицу истинности для всех возможных вариантов.
   

   x	y	z	F
   0	1	0	0
   1	0	1	0
   1	1	0	0

4. 
   Из получившейся таблицы истинности мы видим, что только одна строка этой таблицы содержит 2 нуля и одну 1 в исходных данных. Эта единица – переменная y, значит третий столбец y. Среди столбцов только один содержит два нуля – столбец z. Отсюда следует, что первый столбец – z.
   
5. 
   Ответ: zxy
   

---

Решение (метод исключения, С.Н. Лукин, г. Москва):

1. 
   всего возможно 6 вариантов решения задачи:
   

x	y	z
x	z	y
y	x	z
y	z	x
z	x	y
z	y	x

В процессе решения будем вычеркивать лишние варианты, пока не останется один-единственный. Также будем по возможности заполнять пустые клетки таблицы (по принципу «Чем меньше неопределенностей, тем лучше»).

2. 
   используем следующее свойство импликации: выражение ab равно нулю тогда и только тогда, когда a=1 и b=0. В нашем примере a это левая скобка, b – правая.
   
3. 
   теперь рассуждаем от противного. Пусть в пустой клетке первой строки таблицы истинности стоит ноль:
   

   ?	?	?	F
   0	0	0	0

4. 
   Тогда в любом из 6 вариантов решения получится x = 0 и y = 0, а значит (x  y)=0, что противоречит упомянутому свойству импликации. Значит, там стоит единица:
   

   ?	?	?	F
   0	0	1	0
   0			0

5. 
   По той же причине в левых двух столбцах первой строки не могут находиться одновременно x и y. Это позволяет нам вычеркнуть два из шести вариантов решения:
   

x	y	z
y	x	z

---

Остаются 4 варианта:

x	z	y
y	z	x
z	x	y
z	y	x

6. 
   Идем дальше. По упомянутому свойству импликации вторая скобка должна равняться 0, а значит y и z не должны совпадать. Это позволяет нам, погдядев на первую строку таблицы истинности, вычеркнуть еще два варианта решения:
   

y	z	x
z	y	x

Остаются 2 варианта:

x	z	y
z	x	y

7. 
   Получается, что в правом столбце обязательно стоит y. Начало положено.
   
8. 
   Попробуем заполнить пустые клетки во второй строке таблицы истинности. Способов заполнения четыре: 00, 01, 10, 11. Первый из них мы рассмотрели выше, он отпадает. Второй отпадает, так как в этом случае две строки таблицы истинности будут совпадать, что противоречит условию задачи. Третий и четвертый способы приказывают нам иметь во втором столбце единицу. Спасибо и на этом:
   

   ?	?	y	F
   0	0	1	0
   0	1		0

9. 
   Теперь рассмотрим первый из двух оставшихся вариантов решения (xzy), подставив сначала в пустую клетку ноль. Но ноль отпадает, так как x и y не могут одновременно равняться нулю. А единица отпадает, так как y и z не должны совпадать. Значит, отпадает и сам вариант решения xzy. Следовательно, решением задачи является единственный невычеркнутый вариант: zxy.
   
10. 
    Из тех же соображений, что y и z не должны совпадать, в оставшуюся пустую клетку ставим единицу:
    

    z	x	y	F
    0	0	1	0
    0	1	1	0

11. 
    А теперь проверьте решение, подставив в выражение (x  y)  (y  z) значения переменных из каждой строки таблицы.
    
12. 
    Ответ: zxy.
    

---

Решение (метод инверсии, А.Н. Носкин, г. Москва):

1. 
   Известно, что если F = 0, то обратная её функция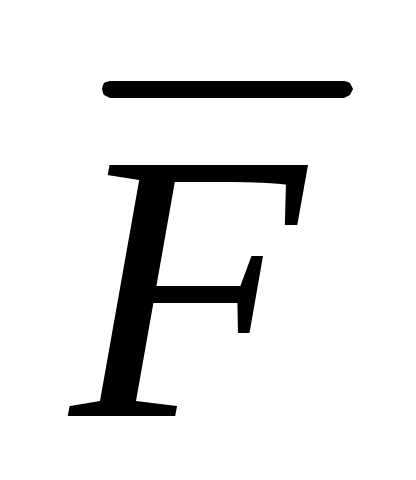 =1.
   
2. 
   Применим закон де Моргана и упростим:
   

3. 
   тогда при тех же значениях аргументов функция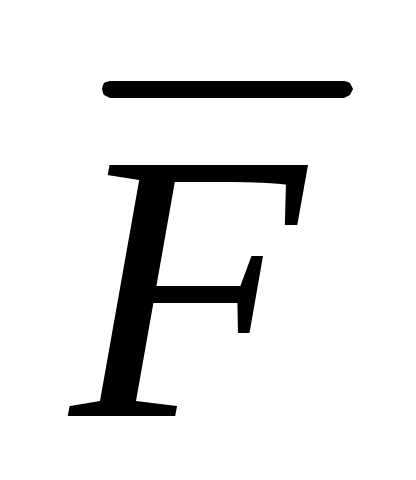 истинна
   

   ?	?	?
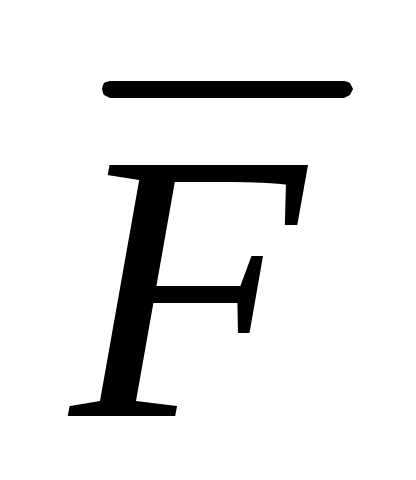
   0	0		1
   0			1

4. 
   анализ формулы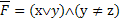 показывает, что для истинности функции 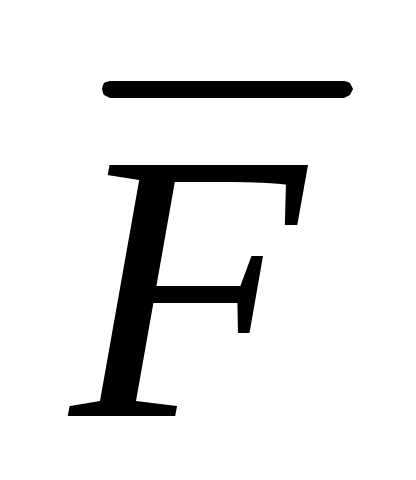необходимо, чтобы значение в каждой скобке были равны 1.
   
5. 
   Кроме того, этот анализ показывает, что в первой строке таблицы, в ее последнем столбце, не может быть 0, так как тогда значение функции не будет равно 1. На основе этого анализа таблица примет вид:
   

?	?	?
0	0	1	1
0			1

6. 
   Анализ первой строки данной таблицы показывает, что в первых двух ячейках не может быть одновременно ни x, ни y. В этих ячейках рядом может быть только x и z, значит y находится в последней ячейке.
   
7. 
   Во второй ячейке, второй строки не может быть 0, так как должны быть неповторяющиеся строки, а все нули быть не могут (не выполнится условие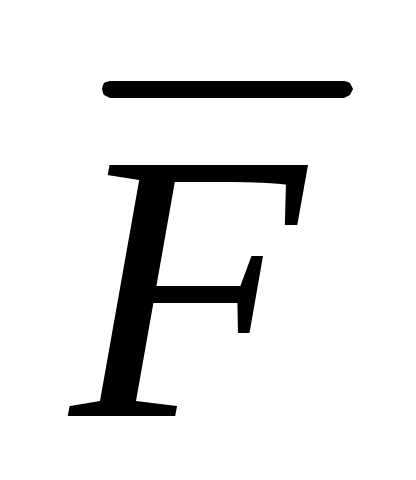 =1). Значит в данной ячейке строго 1.
   

---

?	?	y
0	0	1	1
0	1		1

8. 
   Значит в оставшейся ячейке может быть только 0 или 1, а именно, во второй строке возможен набор 010 или 011. Простой анализ с учетом того, что в последнем столбце y, дает итоговый ответ – набор 011 .
   
9. 
   Ответ: zxy.
   

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx