и построим логическое выражение для заданной функции, обозначив переменные через a, b и с (см. § 22 из учебника для 10 класса):

2. 
   Упрощаем это выражение, используя законы алгебры логики:
   

3. 
   Сравнивая полученное выражение с заданным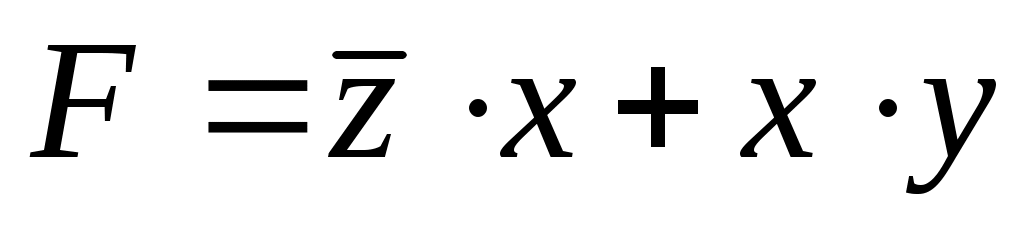 , находим, что a = z, b = y и c = x.
   
4. 
   Ответ: zyx.
   

Решение (сопоставление таблиц истинности, М.С. Коротков):

1. 
   Рассмотрим строки таблицы, где функция равна 1, обозначив переменные через a, b и с
   

a	b	c	F
0	0	1	1
0	1	1	1
1	1	1	1

и сопоставим эти строки с теми строками таблицы истинности заданной функции , где F = 1:

x	y	z	F
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

---

2. 
   Сравнивая столбцы интересующих нас строк, определяем, что c = x (все три единицы в зеленых ячейках), b = y (один ноль и две единицы) и a = z (два ноля и единица).
   
3. 
   Ответ: zyx.
   

Решение (М.В. Кузнецова, через приведение к СДНФ):

1. 
   Функция задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:
   a ∙ 1 = a и .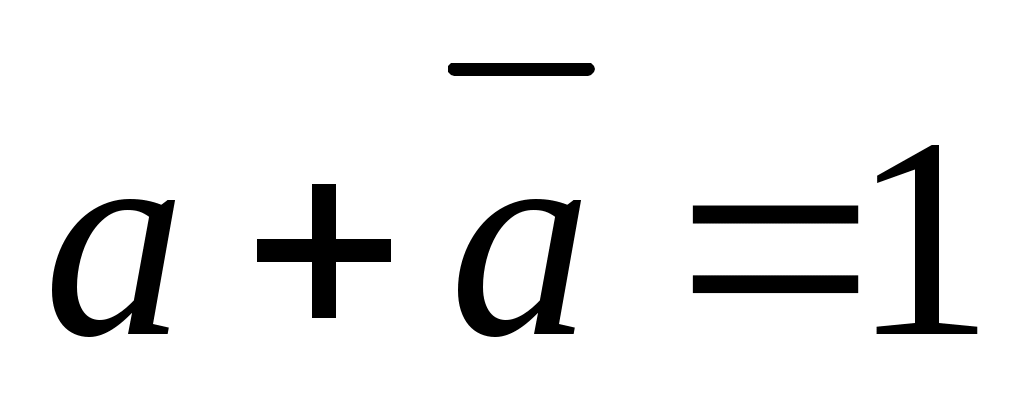
   

Каждую конъюнкцию дополним недостающей переменной:



СДНФ:

2. 
   Каждая конъюнкция в СДНФ соответствует строке таблицы истинности, в которой F=1. Используя полученную СДНФ, делаем вывод: в таблице истинности имеется 3 строки, где F=1, заполним их:
   

	x	y	z	F
	1	1	0	1
	1	0	0	1
	1	1	1	1

3. 
   В таблице, приведенной в задании, рассмотрим строки, где F=1:
   

   ?	?	?	F
   0	0	1	1
   0	1	1	1
   1	1	1	1

4. 
   Сравнивая столбцы этих таблиц, делаем выводы:
   
   1. 
      в первом (жёлтом) столбце таблицы задания находится z (одна единица),
      
   2. 
      во втором (синем) столбце таблицы задания находится y (две единицы),
      
   3. 
      в последнем (зелёном) столбце таблицы задания находится x (все единицы).
      
5. 
   Ответ: zyx.
   

---

---

Ещё пример задания:

Р-13. Каждое логическое выражение A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения A  B?

Решение:

1. 
   полная таблица истинности каждого выражения с пятью переменными содержит 2⁵ = 32 строки
   
2. 
   в каждой таблице по 4 единицы и по 28 (= 32 – 4) нуля
   
3. 
   выражение A  B равно нулю тогда и только тогда, когда A = 0 и B = 1
   
4. 
   минимальное количество единиц в таблице истинности выражения A  B будет тогда, когда там будет наибольшее число нулей, то есть в наибольшем количество строк одновременно A = 0 и B = 1
   
5. 
   по условию A = 0 в 28 строках, и B = 1 в 4 строках, поэтому выражение A  B может быть равно нулю не более чем в 4 строках, оставшиеся 32 – 4 = 28 могут быть равны 1
   
6. 
   Ответ: 28.
   

Ещё пример задания:

Р-12. Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	F
0	0	1	0	0	0
1	0	1	0	1	1
0	1	1	1	0	1

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x1 не совпадает с F.

Решение:

1. 
   полная таблица истинности выражения с пятью переменными содержит 2⁵ = 32 строки
   
2. 
   в приведённой части таблицы в двух строках значение x1 совпадает с F, а в одной – не совпадает
   
3. 
   во всех оставшихся (неизвестных) 32 – 3 = 29 строках значения x1 и F могут не совпадать
   
4. 
   всего несовпадающих строк может быть 1 + 29 = 30.
   
5. 
   Ответ: 30.
   

---

Ещё пример задания:

Р-11. Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:

x1	x2	x3	x4	x5	x6	x7	x8	F
	0						1	0
1			0					1
			1				1	1

Каким выражением может быть F?

1) x1  ¬x2  x3  ¬x4  x5  x6  ¬x7  ¬x8

2) x1  x2  x3  ¬x4  ¬x5  ¬x6  ¬x7  ¬x8

3) ¬x1  x2  ¬x3  x4  x5  ¬x6  ¬x7  ¬x8

4) x1  ¬x2  x3  ¬x4  ¬x5  ¬x6  ¬x7  ¬x8

Решение:

1. 
   перепишем выражения в более простой форме, заменив «И» () на умножение и «ИЛИ» () на сложение:
   

1)

2)

3)

4)

2. 
   в последнем столбце таблицы истинности видим две единицы, откуда сразу следует, что это не может быть цепочка операций «И» (конъюнкций), которая даёт только одну единицу; поэтому ответы 1 и 3 заведомо неверные
   
3. 
   анализируем первую строку таблицы истинности; мы знаем в ней только два значения -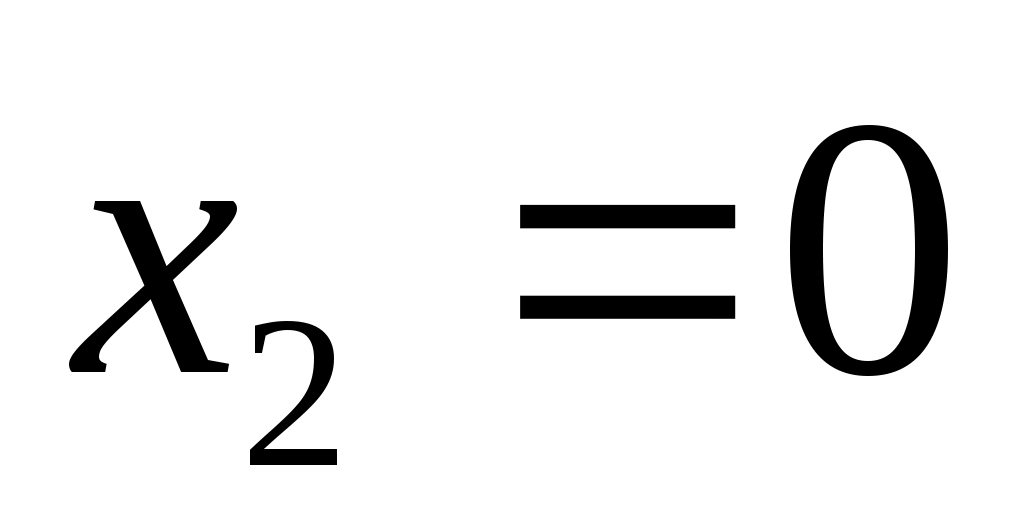 и
   
4. 
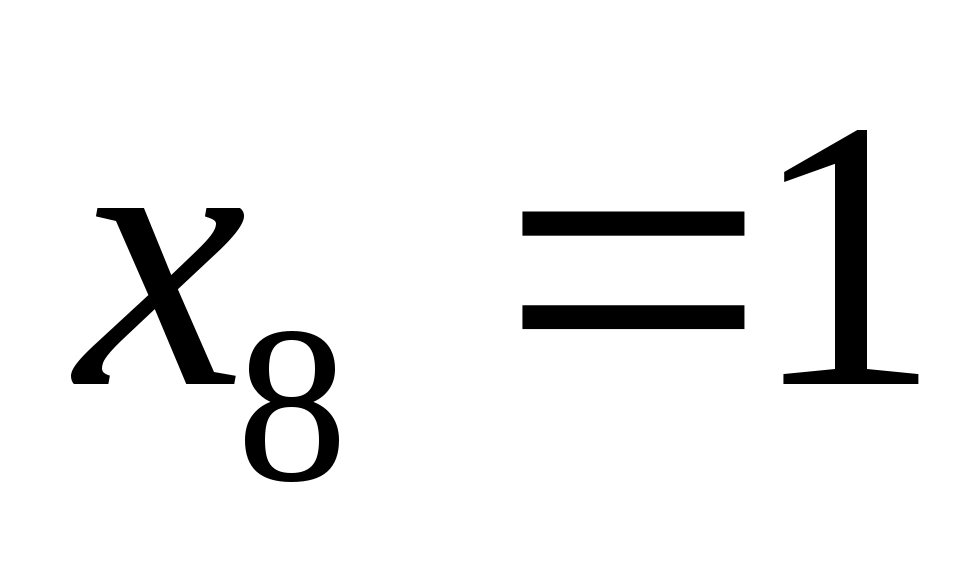
   для того, чтобы в результате в первой строке получить 0, необходимо, чтобы переменная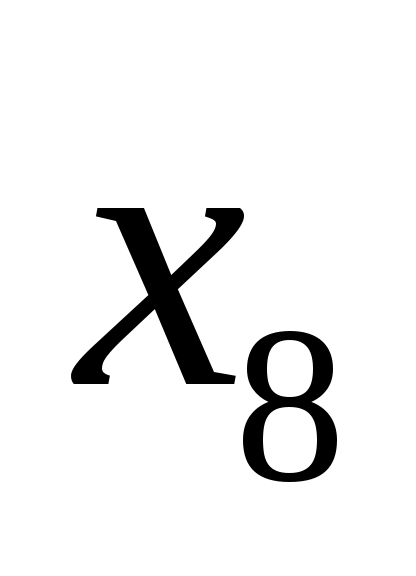 входила в сумму с инверсией (тогда из 1 получится 0!), это условие выполняется для обоих оставшихся вариантов, 2 и 4
   
5. 
   кроме того, переменная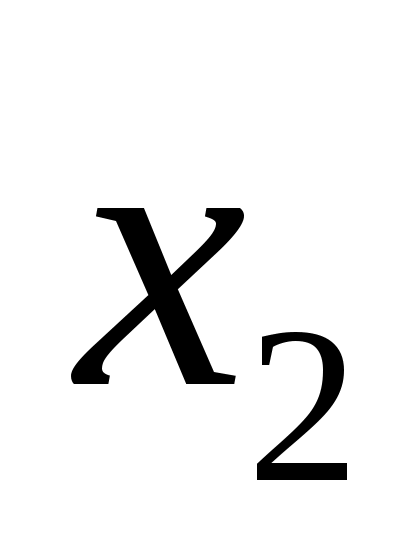 должна входить в выражение без инверсии (иначе соответствующее слагаемое в первой строке равно 1, и это даст в результате 1); этому условию не удовлетворяет выражение 4; остается один возможный вариант – выражение 2
   
6. 
   Ответ: 2.
   

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx