ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 461
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ещё пример задания:
Р-17. Логическая функция F задаётся выражением ¬x y (¬z w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| ? | ? | ? | ? | F |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
-
запишем выражение в более понятной форме: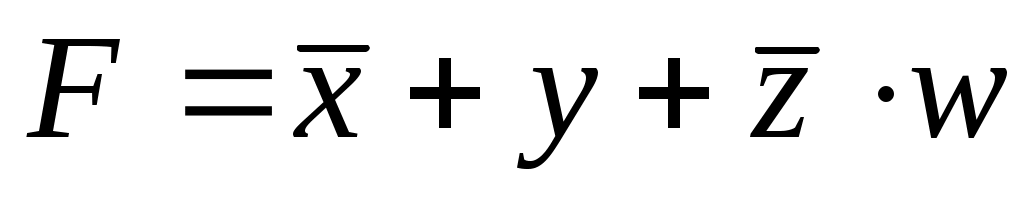
-
анализ формулы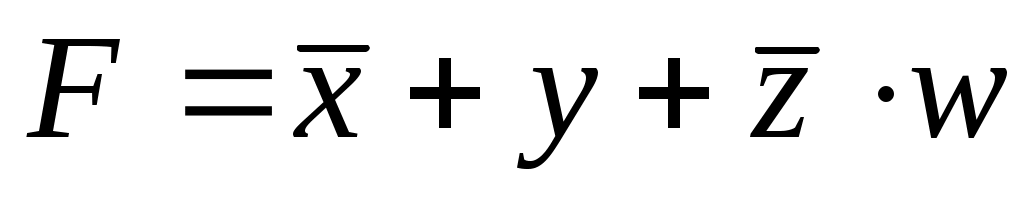 показывает, что для того, чтобы функция F была ложна, необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
y
?
?
x
F
0
0
0
1
0
0
1
0
1
0
0
1
1
1
0
-
остается разобраться с двумя средними столбцами; обратим внимание на вторую строчку таблицы, в которой одна из оставшихся переменных равна 1, а вторая – 0; так как функция равна 0, то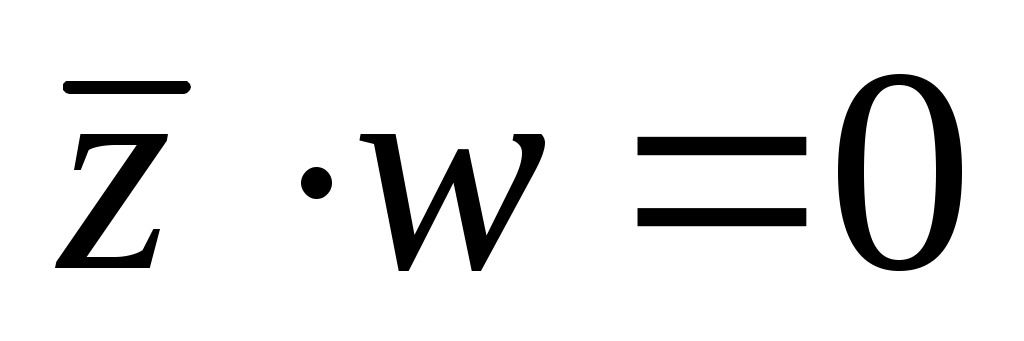
, откуда следует, что z = 1 и w = 0 (иначе произведение будет равно 1) -
Ответ: yzwx.
Решение (2 способ, инверсия выражения):
-
запишем выражение в более понятной форме:
-
попытаемся свести задачу к уже известной задаче; если при каком-то наборе аргументов функция F ложна, то обратная её функция,
, истинна -
построим обратную функцию, используя законы де Моргана:
-
тогда при тех же значениях аргументов функция истинна
?
?
?
?
0
0
0
1
1
0
1
0
1
1
0
1
1
1
1
-
анализ формулы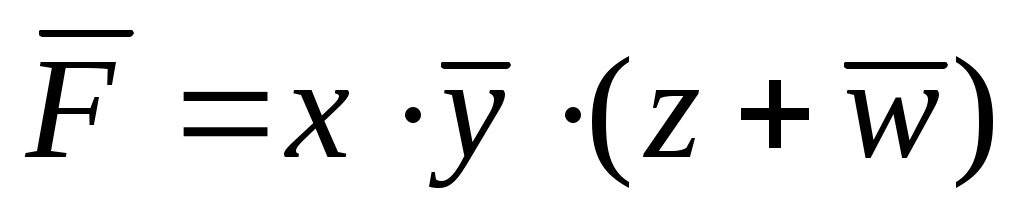
показывает, что для истинности функции необходимо, чтобы x всегдабыл равен 1, а y всегдабыл равен 0; поэтому x – это последний столбец в таблице, а y – первый:
y
?
?
x
0
0
0
1
1
0
1
0
1
1
0
1
1
1
1
-
остается разобраться с двумя средними столбцами; обратим внимание на вторую строчку таблицы, в которой одна из оставшихся переменных равна 1, а вторая – 0; так как функция равна 1, то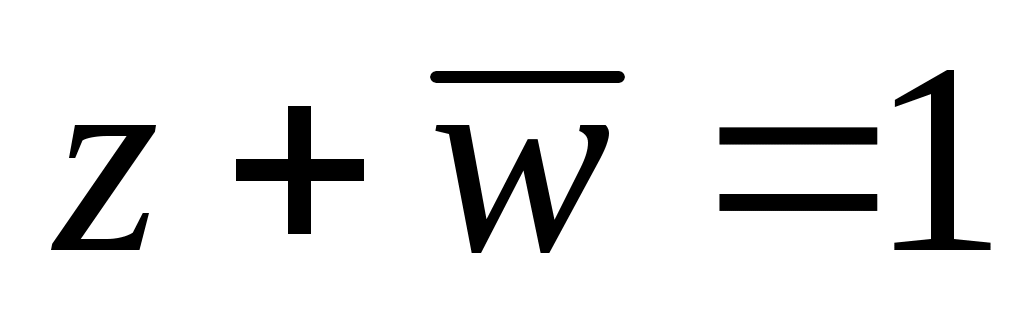
, откуда следует, что z = 1 и w = 0 (иначе сумма будет равна 0) -
Ответ: yzwx.
Ещё пример задания:
Р-16. Логическая функция F задаётся выражением (x y ) (y z). Ниже приведён фрагмент таблицы истинности. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z?
| ? | ? | ? | F |
| 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
Решение:
-
Выражение представляет собой логическое произведение имплкаций. Поэтому для его истинности обе импликации должны быть истинны. -
Расмотрим верхнюю строчку таблицы, где функция принимает значение 1. Здесь одна из переменных равна 0, а две другие равны 1. -
Нулю в этой строке может быть равна только переменная x, так как при y = 0 получаем
(1 0 ) (0 1) = 0 1 = 0
а при z = 0 имеем (1 1 ) (1 0) = 1 0 = 0, то есть эти два варианта не подходят.
Таким образом, второй стоблец – x.
-
Теперь рассматриваем вторую строку, где мы должны получить 0. Мы уже знаем, что второй столбец – x, поэтому во второй строке x = 0, и (0 y ) (y z) = 0. -
Первая импликация 0 y = 1 независимо от значения y. Поэтому для того, чтобы все выражение было равно 0, нужно обеспечить y z = 0. -
Это условие сразу даёт y = 1 и z = 0. Поэтому третий столбец – y, а первый – z. -
Ответ: zxy.
Ещё пример задания (М.В. Кузнецова):
Р-15. Логическая функция F задаётся выражением (x ¬y ¬z) (¬x y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z?
| | ? | ? | ? | F |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение (М.В. Кузнецова, через СКНФ и сопоставление таблиц истинности):
-
Запишем заданное выражение в более простых обозначениях:
-
Функция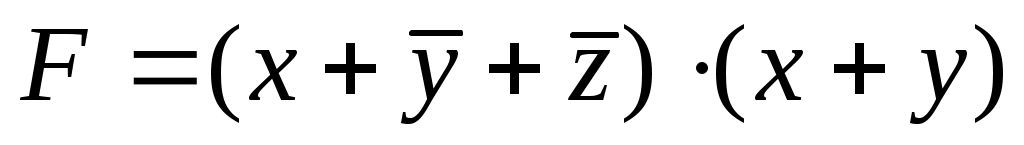 задана в виде КНФ (конъюнктивной нормальной формы), которую можно привести к СКНФ, используя известные тождества алгебры логики: 
, 
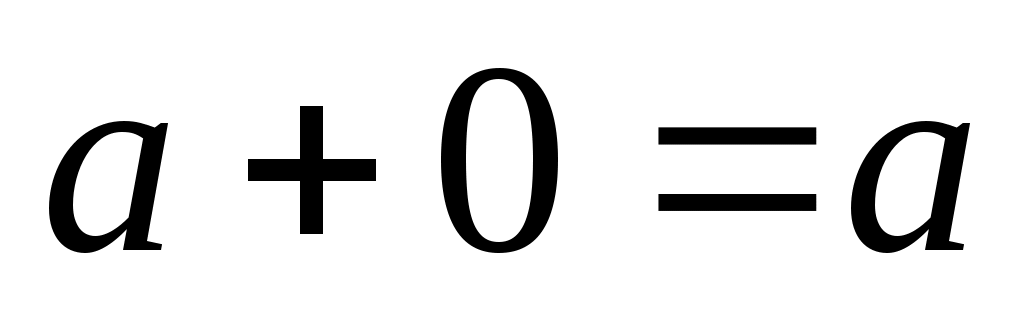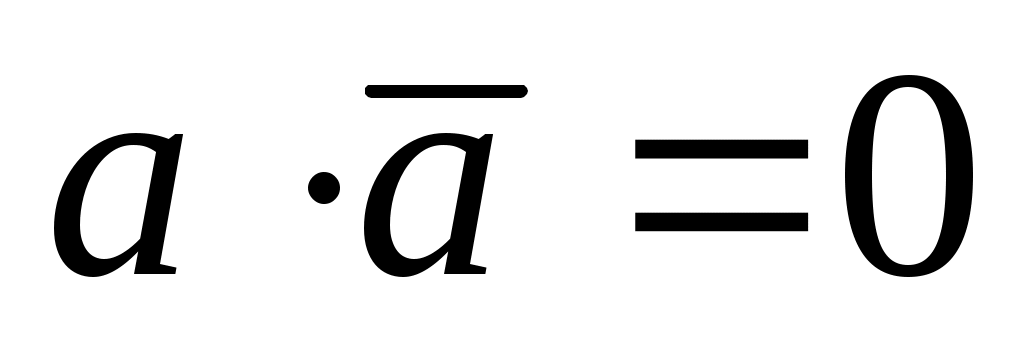и распределительный закон для операции «И» 
.
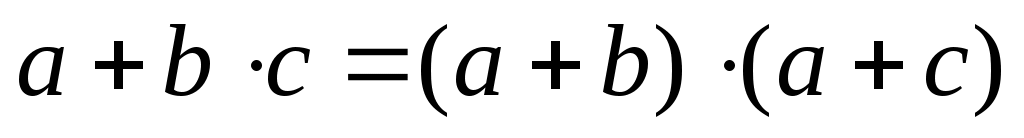Вторую дизъюнкцию дополним недостающей переменной z:
СКНФ:
-
Каждая дизъюнкция в СКНФ соответствует строке таблицы истинности, в которой F=0. Используя полученную СДНФ, делаем вывод: в таблице истинности имеется 3 строки, где F=0, заполним их:
| | x | y | z | F |
 | 0 | 1 | 1 | 0 |
 | 1 | 0 | 0 | 0 |
 | 1 | 0 | 1 | 0 |