ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 93
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ

Лабораторные работы по дисциплине
Структуры и алгоритмы обработки данных
Выполнил: студент гр. З-20-ИВТ-по-Б
Шведов Игорь Михайлович
Зачетная книжка №20.2029
_____________________
Подпись студента
Проверил: Трубаков А.О.
«___» _______________ 20__ г.
_____________________
Подпись преподавателя
Брянск 2022
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ 3
1. ЛАБОРАТОРНАЯ РАБОТА №1 4
1.1. Задание 4
1.2. Решение 4
1.3. Демонстрация программы 8
2. ЛАБОРАТОРНАЯ РАБОТА №2 10
2.1. Задание 10
2.2. Решение 10
2.3. Демонстрация программы 15
3. ЛАБОРАТОРНАЯ РАБОТА №3 21
3.1. Задание 21
3.2. Решение 21
3.3. Демонстрация программы 26
4. ЛАБОРАТОРНАЯ РАБОТА №4 31
4.1. Задание 31
4.2. Решение 31
4.3. Демонстрация программы 36
5. ЛАБОРАТОРНАЯ РАБОТА №5 39
5.1. Задание 39
5.2. Решение 39
5.3. Демонстрация программы 44
6. ЛАБОРАТОРНАЯ РАБОТА №6 52
6.1. Задание 52
6.2. Решение 52
6.3. Демонстрация программы 56
1. ЛАБОРАТОРНАЯ РАБОТА №1
1.1. Задание
Имеется два текстовых файла. В первом из них содержится некоторое описание. Переносы слов допускаются. Второй файл содержит список слов, не подлежащих разглашению. Требуется переписать первый файл, заменив каждое из подобных слов точками.
1.2. Решение
Эта и следующие программы написаны на С++ в Visual Studio 2015. Ниже представленная программа учитывает не только допущение переносов слов, но и различные особенности текстов, которые могут потенциально доставить неприятности для программистов. Это то, что слова могут быть с большой буквы, около слова могут быть знаки препинания, а также то, что одно слово может включать другое как подстроку. Например, если требуется заменить точками слово «генерал», нужно обеспечить, чтобы, к примеру, слово «генеральный» не было никак изменено.
#include
#include
#include
#include
#define MAX_STRLEN 100 // макс. длина строки в файле
#define MAX_STRCNT 20 // макс. число строк в файле
#define FAIL -1 // значение, соответствующее неуспешному поиску
using namespace std;
char ToLower(char c) // приведение к нижнему регистру
{
if (c >= 'А' && c <= 'Я')
return c + 'а' - 'А';
return c;
}
bool IsLetter(char c) // является ли символ буквой?
{
if (c <= 'я' && c >= 'а') return true;
if (c <= 'Я' && c >= 'А') return true;
return false;
}
// содержит ли строка str символ c?
bool Contains(char str[], char c)
{
for (int i = 0; str[i] != 0; i++)
if (str[i] == c)
return true;
return false;
}
// является ли index-ый символ началом слова?
bool IsStartOfWord(char str[], int index)
{
// если не буква, то не начало
if (IsLetter(str[index]) == false) return false;
// если буква и первая в тексте, то начало
if (index == 0) return true;
// если буква и не первая в тексте, то смотря что левее
return Contains("!?.,;: ", str[index - 1]);
}
// является ли index-ый символ концом слова?
bool IsEndOfWord(char str[], int index)
{
// если не буква, то нет
if (IsLetter(str[index]) == false) return false;
int n = strlen(str);
// если это буква и она в конце строки, то является
if (index == n - 1) return true;
// иначе - смотря что справа
return Contains("!?.,;: ", str[index + 1]);
}
// прочесть файл
int ReadFile(char FileName[], char str[MAX_STRCNT][MAX_STRLEN + 1])
{
int n = 0;
ifstream f(FileName, ios::in);
while (f.eof() == false) // пока не найден конец файла
{
// читать строку файла
f.getline(str[n], MAX_STRLEN + 1, '\n');
n++; // увеличить счётчик строк
}
f.close();
return n;
}
// показать содержимое массива строк
void ShowStrings(char str[MAX_STRCNT][MAX_STRLEN + 1], int n)
{
for (int i = 0; i < n; i++)
cout << str[i] << endl;
}
// объединить строки массива в одну
void Linearize(char str[MAX_STRCNT][MAX_STRLEN + 1], int n, char buffer[])
{
int pos = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; str[i][j] != 0; j++)
{
buffer[pos] = str[i][j];
pos++;
}
}
buffer[pos] = 0;
}
// определить длину каждой строки в массиве
void GetStrLens(char str[MAX_STRCNT][MAX_STRLEN + 1], int n, int Lens[])
{
for (int i = 0; i < n; i++)
Lens[i] = strlen(str[i]);
}
// находится ли слово в строке str, начиная с позиции str_index?
int WordIsFound(char str[], char word[], int str_index)
{
// если str_index - не начало слова, то нет
if (IsStartOfWord(str, str_index) == false) return FAIL;
int str_pos = str_index;
// сверяем символы строки, начиная с str_index,
// и символы слова word
for (int i = 0; word[i] != 0; i++, str_pos++)
{
// если слово длиннее, чем число символов
// от str_index и до конца строки str
if (str[str_pos] == 0) return FAIL;
// перенос не участвует в сравнении символов
if (str[str_pos] == '-') i--;
else
{
// ToLower: слово в тексте может начинаться с большой
// буквы или быть выделено большими буквами
if (ToLower(str[str_pos]) != word[i])
return FAIL;
}
}
// если символ str, соответствующий последней букве word,
// не конец слова: такое бывает, если word - часть слова,
// начинающегося с str_index (с str_index идёт "завал", а word="вал")
if (IsEndOfWord(str, str_pos - 1) == false)
return FAIL;
// вернуть индекс, идущий после вхождения слова в str
return str_pos;
}
// заменить слово, начинающееся с str_index, звёздочками
void KillWord(char str[], char word[], int str_index)
{
int str_pos = str_index;
for (int i = 0; word[i] != 0; i++, str_pos++)
{
if (str[str_pos] == '-') i--;
str[str_pos] = '.';
}
}
// обработка по позиции str_index
int ProcessPosition(char str[], char list[MAX_STRCNT][MAX_STRLEN + 1], int nList,
int str_index)
{
for (int i = 0; i < nList; i++) // идём по списку слов
{
int next = WordIsFound(str, list[i], str_index);
if (next != FAIL) // если по позиции str_index слово list[i]
{
// заменяем звёздочками
KillWord(str, list[i], str_index);
return next; // возвращаем позицию символа после звёздочек
}
}
// замены не было - дальше требуется обработать следующую позицию
return str_index + 1;
}
// главная функция обработки строки
void ProcessStr(char str[], char list[MAX_STRCNT][MAX_STRLEN + 1], int nList)
{
int str_index = 0;
while (str[str_index] != 0)
{
str_index = ProcessPosition(str, list, nList, str_index);
}
}
// по строке и массиву длин разбить строку на несколько
void RestoreStrs(char str[], int Lens[], int n, char Text[MAX_STRCNT][MAX_STRLEN + 1])
{
char * ptr = str;
for (int i = 0; i < n; i++)
{
char end = ptr[Lens[i]];
ptr[Lens[i]] = 0;
strcpy_s(Text[i], MAX_STRLEN, ptr);
ptr[Lens[i]] = end;
ptr += Lens[i]; // смещение указателя на Lens[i] позиций
}
}
// запись текста в файл
void WriteText(char FileName[], char Text[MAX_STRCNT][MAX_STRLEN + 1], int n)
{
ofstream file(FileName, ios::out);
for (int i = 0; i < n; i++)
{
file << Text[i];
if (i < n - 1) file << endl;
}
file.close();
}
void main()
{
setlocale(LC_ALL, "rus");
char FileText[20], FileList[20];
cout << "Введите имя файла с текстом: ";
cin >> FileText;
cout << "Введите имя файла со списком: ";
cin >> FileList;
char text[MAX_STRCNT][MAX_STRLEN + 1];
char list[MAX_STRCNT][MAX_STRLEN + 1];
int nText = ReadFile(FileText, text); // прочитать текст
int nList = ReadFile(FileList, list); // прочитать список слов
cout << endl << "Содержимое файла " << FileText << endl;
cout << "______________________________________" << endl;
ShowStrings(text, nText);
cout << endl << "Содержимое файла " << FileList << endl;
cout << "______________________________________" << endl;
ShowStrings(list, nList);
char Linear[MAX_STRCNT * MAX_STRLEN + 1];
// привести массив строк к единой строке
Linearize(text, nText, Linear);
// обработать эту строку
ProcessStr(Linear, list, nList);
int lens[MAX_STRCNT];
// определить длины строк в тексте
GetStrLens(text, nText, lens);
// восстановить массив строк по строке
RestoreStrs(Linear, lens, nText, text);
cout << endl << "Измененный текст: " << endl;
cout << "______________________________________" << endl;
ShowStrings(text, nText);
// записать текст в файл
WriteText(FileText, text, nText);
_getch();
}
1.3. Демонстрация программы
Вид исходных текстовых файлов и окна программы:
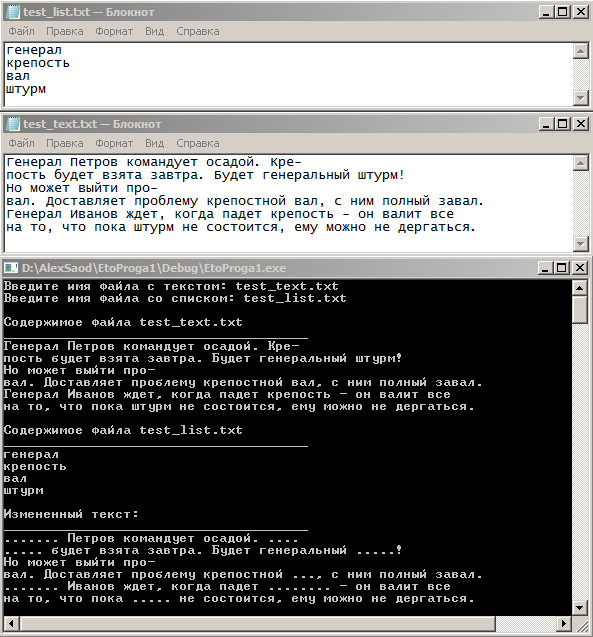
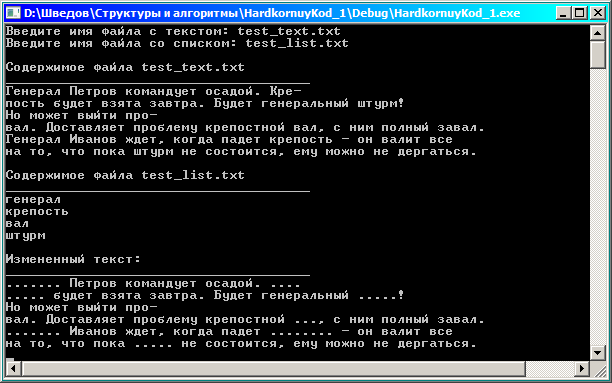
Как видно, не возникает проблем, связанных с разными регистрами, словами, которые часть других слов, переносами.
Вид измененного файла:
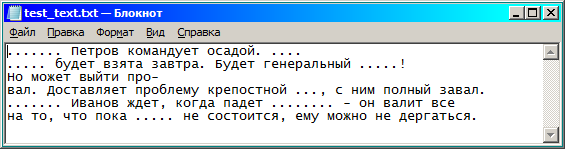
2. ЛАБОРАТОРНАЯ РАБОТА №2
2.1. Задание
В некотором институте приобретаемые компьютеры выделяются различным факультетам поочередно. В пределах факультета имеются очереди из кафедр. Факультет, получивший компьютер, перемещается в конец очереди, а соответствующая кафедра исключается из факультетской очереди. Вновь организованные факультеты и кафедры занимают последние места в соответствующих очередях. Составить программу ведения очереди на компьютеры.
2.2. Решение
#include
#include
#include
#define MAXSZ 9 // максимальный размер строки
using namespace std;
// белый цвет текста
int white_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_RED | FOREGROUND_INTENSITY;
// голубой цвет текста
int cyan_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_INTENSITY;
// получаем дескриптор для устройства вывода
HANDLE handle = GetStdHandle(STD_OUTPUT_HANDLE);
void SetColor(int color)
{
// установка цвета текста
SetConsoleTextAttribute(handle, color);
}
struct Chair // структура КАФЕДРА
{
char Name[MAXSZ]; // имя
Chair * next; // следующая кафедра из списка
// конструктор
Chair(char NameOfChair[])
{
strcpy_s(this->Name, MAXSZ, NameOfChair);
this->next = NULL;
}
};
struct Faculty // структура ФАКУЛЬТЕТ
{
char Name[MAXSZ]; // имя
Chair * head, *tail; // голова и хвост списка кафедр
Faculty * next; // следующий факультет в списке факультетов (т.е. очереди)
// конструктор
Faculty(char FacName[])
{
strcpy_s(this->Name, MAXSZ, FacName);
head = NULL;
tail = NULL;
next = NULL;
}
void AddChair(char ChairName[]); // добавление кафедры в конец факультетской очереди
void RemoveChair(); // удаление кафедры из головы факультетской очереди
void Print(); // вывод факультетской очереди на экран
};
void Faculty::AddChair(char ChairName[])
{
// добавление кафедры
Chair * Additional = new Chair(ChairName);
if (this->head == NULL) // особая ситуация - когда очередь пуста
{
this->head = Additional;
this->tail = this->head;
return;
}
this->tail->next = Additional;
this->tail = Additional;
}
void Faculty::RemoveChair()
{
// удаление первой кафедры из очереди
if (this->head == NULL) return;
Chair * q = this->head->next;
delete[](this->head);
this->head = q;
if (q == NULL) this->tail = NULL;
}
void Faculty::Print() // выводим факультетскую очередь на экран
{
if (this->head == NULL) // особая ситуация - когда очередь пуста
{
cout << "\n На факультете " << (this->Name) << " нет кафедр, нуждающихся в компьютерах";
return;
}
cout << "\n Очередь факультета " << (this->Name) << ": ";
Chair * cur = this->head;
// для непустой очереди бежим по списку, выводя содержимое узлов
while (cur)
{
cout << (cur->Name);
if (cur->next) cout << ", ";
cur = cur->next;
}
}
struct Queue // структура ОЧЕРЕДЬ
{
Faculty * head, *tail; // голова и хвост списка (очереди) факультетов
Queue() { head = NULL; tail = NULL; } // конструктор
void AddFaculty(char FacName[], char NewChair[]); // добавление факультета
bool AddChair(char FacultyName[], char ChairName[]); // добавление кафедры
void ToTail(); // перенос головного элемента в хвост очереди факультетов
void OneComp(); // вспомогательная функция удаления из очереди
void NewComp(); // основная функция удаления из очереди
void Print(); // вывод очереди на экран
};
void Queue::AddFaculty(char FacName[], char NewChair[])
{
/* ! смысл второго параметра: сразу же организуем на новом факультете первую
кафедру; факультетов без кафедр не бывает */
Faculty * NewFacl = new Faculty(FacName); // создаём факультет
NewFacl->AddChair(NewChair); // создаём кафедру
// помещаем факультет в очередь
if (this->head == NULL)
{
this->head = NewFacl;
this->tail = this->head;
return;
}
this->tail->next = NewFacl;
this->tail = NewFacl;
}
bool Queue::AddChair(char FacultyName[], char ChairName[])
{
Faculty * cur = this->head;
// ищем в очереди факультет, к которому относится кафедра
while (cur)
{
if (strcmp(cur->Name, FacultyName) == 0)
{
// в очередь найденного факультета добавляем кафедру
cur->AddChair(ChairName);
return true;
}
cur = cur->next;
}
// здесь окажемся, если был указан отсутствующий в списке факультет
return false;
}
void Queue::ToTail()
{
// перемещение в хвост очереди
/* особые условия - пустая очередь и очередь из 1 элемента */
if (this->head == NULL) return;
if (this->tail == this->head) return;
/* если у нас "правильная" очередь, т.е. хотя бы из 2 элементов */
Faculty * Second = this->head->next;
this->tail->next = this->head;
this->tail = this->head;
this->tail->next = NULL;
this->head = Second;
}
void Queue::OneComp()
{
// выдача компа - вспомогательная функция
if (this->head == NULL) return;
if (this->head->head != NULL)
{
cout << "Комп выдан: " << (this->head->Name) << ", " << (this->head->head->Name) << "\n";
this->head->RemoveChair();
ToTail();
return;
}
ToTail();
OneComp();
}
void Queue::NewComp()
{
// выдача компа - основная функция
bool flag = false;
Faculty * cur = this->head;
while (cur) // ищем первый в списке факультет, которому нужны компы
{
if (cur->head != NULL)
{
flag = true;
break;
}
cur = cur->next;
}
if (flag == false) return;
OneComp(); // вызываем вспомогательную функцию
}
void Queue::Print()
{
// вывод очереди на экран
if (this->head == NULL) // особое условие - компы не нужны никому
{
cout << "\n Нет факультетов, требующих компы";
return;
}
Faculty * cur = this->head;
cout << "\n Очередь: ";
// бежим по списку факультетов
while (cur)
{
cout << endl;
cur->Print(); // выводим факультетскую очередь
cur = cur->next;
}
}
// получение строки с кириллицей
void GetStr(char str[])
{
char buufer[MAXSZ];
cin >> buufer;
OemToChar(buufer, str);
}
void ShowMenu() // функция вывода меню
{
SetColor(cyan_color);
cout << "\n 1 - Дать новый комп, 2 - организовать факультет, 3 - организовать кафедру/добавить кафедру в очередь факультета, ";
cout << "4 - показать очередь, другая клафиша - выход\n\n ";
SetColor(white_color);
}
void main()
{
setlocale(LC_ALL, "rus");
SetColor(white_color);
Queue Q;
char FacName[MAXSZ], ChairName[MAXSZ];
bool flag = true;
while (flag == true)
{
ShowMenu();
int key;
cin >> key;
cout << "Выбрано: " << key << "\n";
switch (key) // действуем в зависимости от нажатой клавиши
{
case 1: /* 1 - поступили компы, выполняется удаление кафедры из очереди
и перемещение факультета в хвост списка факультетов */
{
Q.NewComp();
cout << "Операция выполнена";
}
break;
case 2: /* 2 - организован новый факультет */
{
cout << "Введите имя факультета: ";
GetStr(FacName); // вводится имя факультета
cout << "Добавьте первую кафедру на этот факультет: ";
GetStr(ChairName); // вводится имя первой его кафедры
Q.AddFaculty(FacName, ChairName); // факультет добавляется в очередь
}
break;
case 3: /* 3 - организована новая кафедра */
{
cout << "Введите сокращенное имя кафедры: ";
GetStr(ChairName); // вводится имя кафедры
cout << "Введите сокращенное имя факультета: ";
GetStr(FacName); // вводится имя факультета
// если такого факультета нет, ничего не добавляется
if (Q.AddChair(FacName, ChairName) == false)
cout << "Не могу найти факультет!\n";
}
break;
case 4: /* 4 - показать очередь факультетов и очереди кафедр */
{
Q.Print();
}
break;
default: /* прочее - завершить работу программы */
{
flag = false;
}
}
}
}
2.3. Демонстрация программы
Добавим несколько факультетов и кафедр в изначально пустую очередь:
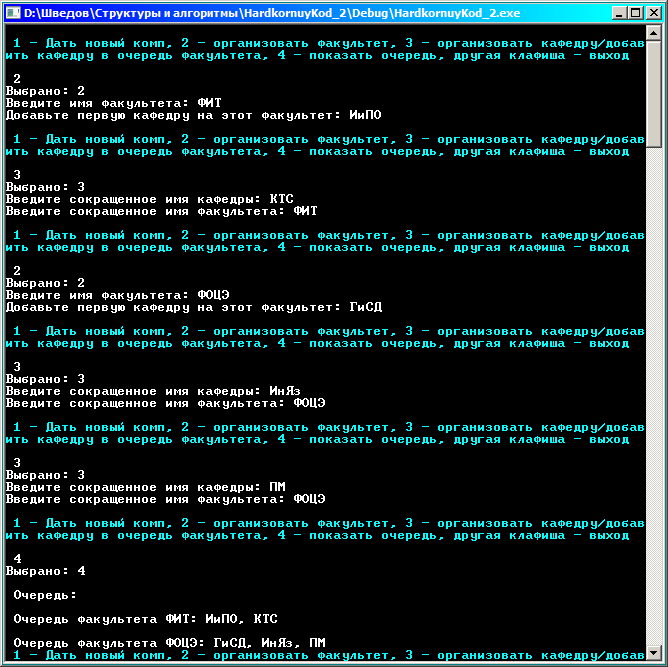
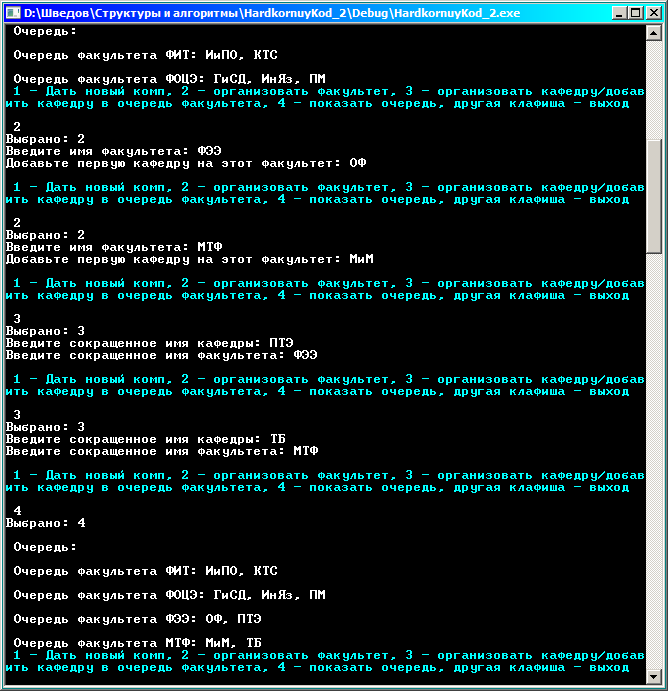
Выполним извлечение из очереди (т.е. имитируем поступление нового компьютера):
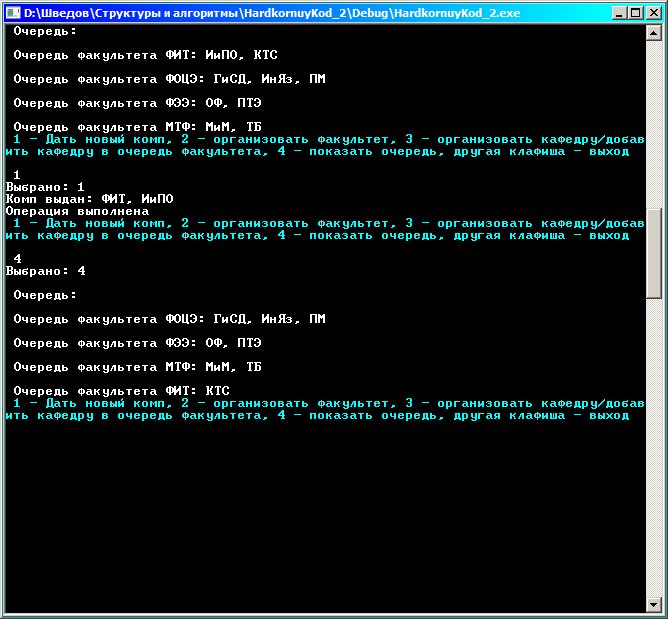
Заметим, что кафедра ИиПО исключилась из очереди факультета ФИТ, а сам факультет ушел в конец очереди факультетов.
Выполним еще одно извлечение:
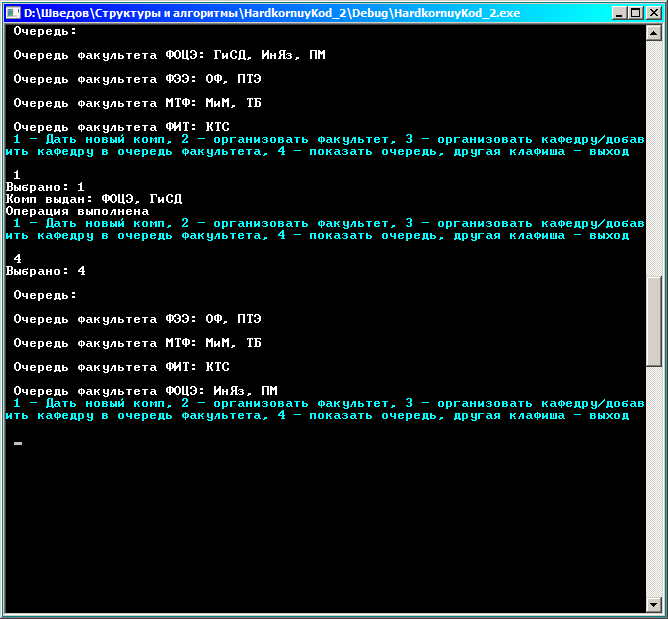
Теперь ГиСД исключена из очереди ФОЦЭ, а сам ФОЦЭ помещен в хвост очереди факультетов.
Добавим кафедру ВМ в очередь факультета ФИТ.
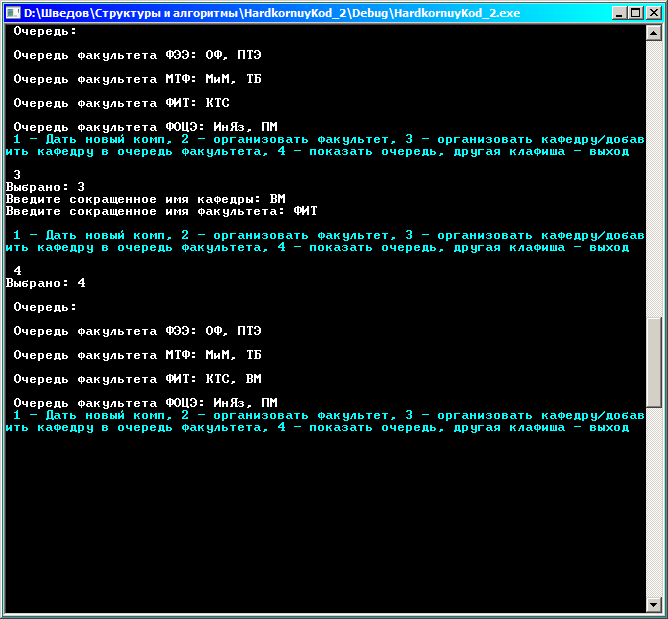
Как и предполагалось:
-
кафедра заняла место в хвосте очереди ФИТ;
-
позиция факультета в очереди факультетов осталась той же.
3. ЛАБОРАТОРНАЯ РАБОТА №3
3.1. Задание
Ввести произвольное сильно ветвящееся дерево. Выдать списки вершин:
1) являющихся листьями;
2) не являющихся листьями;
3) родителей листьев;
4) заданного уровня считая от вершины.
3.2. Решение
Следующая программа не только выполняет заданные операции для сильно ветвящихся деревьев, но и выполняет визуализацию дерева с изображением «веток». Чтение дерева осуществляется из файла. Это сделано, чтобы просто можно было загрузить дерево, не вводя его данные каждый раз заново с клавиатуры.
#include
#include
#include
#include
// спец. значение, которым не может быть индекс в массиве
#define SPECIAL_VALUE -1
using namespace std;
struct Node // структура УЗЕЛ ДЕРЕВА
{
int id; // идентификатор узла
int nKeys; // число ключей узла
int * keys; // ключи
Node ** children; // потомки
Node(int id, int MaxAllowedPower) // конструктор узла
{
this->nKeys = 0;
this->id = id;
// ! если узел не листовой потомков на 1 больше, нежели ключей
this->keys = new int[MaxAllowedPower - 1];
this->children = new Node * [MaxAllowedPower];
for (int i = 0; i < MaxAllowedPower; i++)
this->children[i] = NULL;
}
// является ли листом?
bool IsLeaf() { return (this->children[0] == NULL); }
// операция вывода в поток
friend ostream & operator << (ostream & os, Node & v);
int FindLastChild() // поиск самого правого сына
{
// если узел листовой, детей нет
if (IsLeaf()) return SPECIAL_VALUE;
// если не листовой, используем то, что у нас
// ровно nKeys + 1 детей
return nKeys;
}
// вывод поддерева с корнем this на экран
void PrintTree(int level, // уровень узла
int num_of_child, // каким по счёту сыном своего родителя является узел
bool Vis[] // информация для вывода вертикальных частей веток
);
};
// различные функции условий поиска узлов
bool IsLeaf(Node * v) { return v->IsLeaf(); }
bool IsInternal(Node * v) { return !(v->IsLeaf()); }
bool IsParentOfLeaf(Node * v)
{
if (IsLeaf(v)) // если узел - лист, он точно не родитель листа
return false;
// все листья на одном уровне, потому достаточно
// проверить, является ли 1-ый ребенок листом
return IsLeaf(v->children[0]);
}
ostream & operator << (ostream & os, Node & v)
{
os << "id = " << v.id << ", ключи: ";
for (int i = 0; i < v.nKeys; i++)
{
os << v.keys[i];
// если ключ не последний
if (i < v.nKeys - 1)
os << ", ";
}
return os;
}
void Node::PrintTree(int level, int num_of_child, bool Vis[])
{
for (int j = 0; j < 2; j++)
{
for (int i = 0; i < level - 1; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
if (level > 0)
{
if (j == 1) cout << "|_______";
else cout << "| ";
}
if (j < 1) cout << "\n";
}
// выводим содержимое узла
cout << (*this) << "\n";
if (this->IsLeaf() == true)
{
for (int i = 0; i < level; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
cout << "\n";
return;
}
int lchild = this->FindLastChild();
// рекурсивно вызываем функцию для потомков
for (int i = 0; i <= nKeys; i++)
{
bool Temp[100];
if (level > 0)
copy(Vis, Vis + level, Temp);
Temp[level] = (i != lchild) ? true : false;
if (this->children[i] != NULL)
this->children[i]->PrintTree(level + 1, i, Temp);
}
}
class SVD // класс СИЛЬНОВЕТВЯЩЕЕСЯ ДЕРЕВО
{
int MaxPower; // макс. степень
Node * root; // корень
int count; // счетчик для поиска
// для загрузки одного узла из файла
void LoadNodeFromFile(ifstream * file, Node ** all, int index);
// для загрузки узлов из файла
void LoadNodesFromFile(ifstream * file);
// удаление поддерева
void DelSubtree(Node * rt);
// поиск узлов с заданным условием с сохранением
// их id в массив чисел
void Finder(Node *rt, bool(*Filter)(Node *), int ids[]);
// поиск узлов на заданном уровне
void FindAtLevel(Node * rt, int level, int requiredLevel, int ids[]);
public:
// конструктор с загрузкой из файла
SVD(int MaxPower, char FileName[]);
// вывод дерева
friend ostream & operator << (ostream & os, SVD & derevo);
// поиск по заданному условию
int Finder(bool(*Filter)(Node *), int ids[])
{
count = 0; // пока что ничего не найдено
Finder(root, Filter, ids);
return count; // вернуть число найденных узлов
}
// поиск узлов на заданном уровне
int FindAtLevel(int requiredLevel, int ids[])
{
count = 0; // пока что ничего не найдено
FindAtLevel(root, 0, requiredLevel, ids);
return count; // вернуть число найденных узлов
}
// деструктор
SVD() { DelSubtree(root); }
кафедра заняла место в хвосте очереди ФИТ;
позиция факультета в очереди факультетов осталась той же.
#include
#include
#include
// спец. значение, которым не может быть индекс в массиве
#define SPECIAL_VALUE -1
using namespace std;
struct Node // структура УЗЕЛ ДЕРЕВА
{
int id; // идентификатор узла
int nKeys; // число ключей узла
int * keys; // ключи
Node ** children; // потомки
Node(int id, int MaxAllowedPower) // конструктор узла
{
this->nKeys = 0;
this->id = id;
// ! если узел не листовой потомков на 1 больше, нежели ключей
this->keys = new int[MaxAllowedPower - 1];
this->children = new Node * [MaxAllowedPower];
for (int i = 0; i < MaxAllowedPower; i++)
this->children[i] = NULL;
}
// является ли листом?
bool IsLeaf() { return (this->children[0] == NULL); }
// операция вывода в поток
friend ostream & operator << (ostream & os, Node & v);
int FindLastChild() // поиск самого правого сына
{
// если узел листовой, детей нет
if (IsLeaf()) return SPECIAL_VALUE;
// если не листовой, используем то, что у нас
// ровно nKeys + 1 детей
return nKeys;
}
// вывод поддерева с корнем this на экран
void PrintTree(int level, // уровень узла
int num_of_child, // каким по счёту сыном своего родителя является узел
bool Vis[] // информация для вывода вертикальных частей веток
);
};
// различные функции условий поиска узлов
bool IsLeaf(Node * v) { return v->IsLeaf(); }
bool IsInternal(Node * v) { return !(v->IsLeaf()); }
bool IsParentOfLeaf(Node * v)
{
if (IsLeaf(v)) // если узел - лист, он точно не родитель листа
return false;
// все листья на одном уровне, потому достаточно
// проверить, является ли 1-ый ребенок листом
return IsLeaf(v->children[0]);
}
ostream & operator << (ostream & os, Node & v)
{
os << "id = " << v.id << ", ключи: ";
for (int i = 0; i < v.nKeys; i++)
{
os << v.keys[i];
// если ключ не последний
if (i < v.nKeys - 1)
os << ", ";
}
return os;
}
void Node::PrintTree(int level, int num_of_child, bool Vis[])
{
for (int j = 0; j < 2; j++)
{
for (int i = 0; i < level - 1; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
if (level > 0)
{
if (j == 1) cout << "|_______";
else cout << "| ";
}
if (j < 1) cout << "\n";
}
// выводим содержимое узла
cout << (*this) << "\n";
if (this->IsLeaf() == true)
{
for (int i = 0; i < level; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
cout << "\n";
return;
}
int lchild = this->FindLastChild();
// рекурсивно вызываем функцию для потомков
for (int i = 0; i <= nKeys; i++)
{
bool Temp[100];
if (level > 0)
copy(Vis, Vis + level, Temp);
Temp[level] = (i != lchild) ? true : false;
if (this->children[i] != NULL)
this->children[i]->PrintTree(level + 1, i, Temp);
}
}
class SVD // класс СИЛЬНОВЕТВЯЩЕЕСЯ ДЕРЕВО
{
int MaxPower; // макс. степень
Node * root; // корень
int count; // счетчик для поиска
// для загрузки одного узла из файла
void LoadNodeFromFile(ifstream * file, Node ** all, int index);
// для загрузки узлов из файла
void LoadNodesFromFile(ifstream * file);
// удаление поддерева
void DelSubtree(Node * rt);
// поиск узлов с заданным условием с сохранением
// их id в массив чисел
void Finder(Node *rt, bool(*Filter)(Node *), int ids[]);
// поиск узлов на заданном уровне
void FindAtLevel(Node * rt, int level, int requiredLevel, int ids[]);
public:
// конструктор с загрузкой из файла
SVD(int MaxPower, char FileName[]);
// вывод дерева
friend ostream & operator << (ostream & os, SVD & derevo);
// поиск по заданному условию
int Finder(bool(*Filter)(Node *), int ids[])
{
count = 0; // пока что ничего не найдено
Finder(root, Filter, ids);
return count; // вернуть число найденных узлов
}
// поиск узлов на заданном уровне
int FindAtLevel(int requiredLevel, int ids[])
{
count = 0; // пока что ничего не найдено
FindAtLevel(root, 0, requiredLevel, ids);
return count; // вернуть число найденных узлов
}
// деструктор
};
void SVD::LoadNodeFromFile(ifstream * file, Node ** all, int index)
{
char NodeType[5];
(*file) >> NodeType; // читаем тип узла
(*file) >> all[index]->nKeys; // читаем кол-во ключей
int i;
// читаем ключи
for (i = 0; i < all[index]->nKeys; i++)
(*file) >> all[index]->keys[i];
// если узел внутренний, читаем потомков
if (strcmp(NodeType, "node") == 0)
{
int childId;
// потомков на 1 больше ключей
for (i = 0; i <= all[index]->nKeys; i++)
{
(*file) >> childId;
// -1: нумерация в массиве с 0, а не с 1
all[index]->children[i] = all[childId - 1];
}
}
}
void SVD::LoadNodesFromFile(ifstream * file)
{
int nNodes, rootId;
(*file) >> nNodes;
(*file) >> rootId;
Node ** all = new Node *[nNodes];
int i;
for (i = 0; i < nNodes; i++)
// i+1; у all[0] идентификатор 1, у all[1] = 2...
all[i] = new Node(i + 1, MaxPower);
this->root = all[rootId - 1];
for (i = 0; i < nNodes; i++)
this->LoadNodeFromFile(file, all, i);
}
SVD::SVD(int MaxPower, char FileName[])
{
this->MaxPower = MaxPower;
ifstream file(FileName, ios::in);
LoadNodesFromFile(&file);
file.close();
}
ostream & operator << (ostream & os, SVD & derevo)
{
bool Vis[1];
derevo.root->PrintTree(0, SPECIAL_VALUE, Vis);
return os;
}
void SVD::DelSubtree(Node * rt)
{
// рекурсивное удаление для потомков
for (int i = 0; i <= rt->nKeys; i++)
{
// за указателем NULL не будет используемых ячеек
if (rt->children[i] == NULL) break;
DelSubtree(rt->children[i]);
}
// удаляем массивы ключей и потомков
delete[](rt->keys);
delete[](rt->children);
// удаляем сам узел
delete rt;
}
void SVD::Finder(Node *rt, bool(*Filter)(Node *), int ids[])
{
if (Filter(rt)) // если rt соответствует условию
{
ids[count] = rt->id;
count++;
}
int maxIndex = rt->FindLastChild();
// рекурсивный поиск для потомков
for (int i = 0; i <= maxIndex; i++)
Finder(rt->children[i], Filter, ids);
}
void SVD::FindAtLevel(Node * rt, int level, int requiredLevel, int ids[])
{
if (level == requiredLevel) // если нужный уровень
{
ids[count] = rt->id;
count++;
// ! если узел на нужном уровне, нет смысла искать
// для потомков
return;
}
int maxIndex = rt->FindLastChild();
// рекурсивный поиск для потомков
for (int i = 0; i <= maxIndex; i++)
FindAtLevel(rt->children[i], level + 1, requiredLevel, ids);
}
void ShowArray(int A[], int n)
{
for (int i = 0; i < n; i++)
cout << A[i] << " ";
cout << "\n";
}
void main()
{
setlocale(LC_CTYPE, "rus");
char FileName[15];
cout << "Введите файл с деревом: ";
cin >> FileName;
SVD derevo(4, FileName);
cout << "Дерево\n" << derevo << "\n";
int ids[100]; // для сохранения результатов поиска
int n = derevo.Finder(IsLeaf, ids); // поиск листьев
cout << "id листьев: ";
ShowArray(ids, n);
n = derevo.Finder(IsInternal, ids); // поиск внутренних узлов
cout << "id внутренних узлов: ";
ShowArray(ids, n);
// поиск родителей листьев
n = derevo.Finder(IsParentOfLeaf, ids);
cout << "id родителей листьев: ";
ShowArray(ids, n);
int level;
cout << "Введите искомый уровень: ";
cin >> level;
n = derevo.FindAtLevel(level, ids);
cout << "id вершин на уровне: ";
ShowArray(ids, n);
_getch();
}