ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 100
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3.3. Демонстрация программы
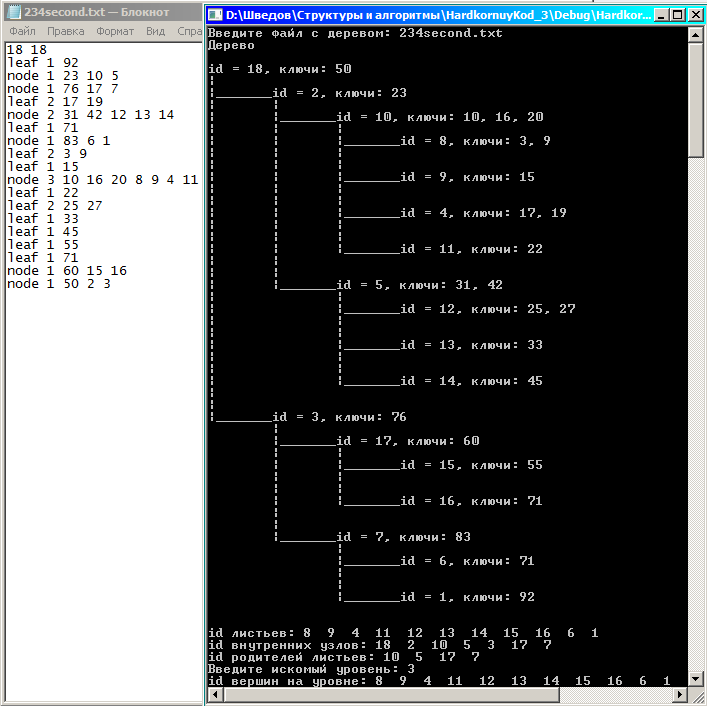
Тестовая коллекция деревьев (напротив каждой вершины поставлен ее идентификатор):
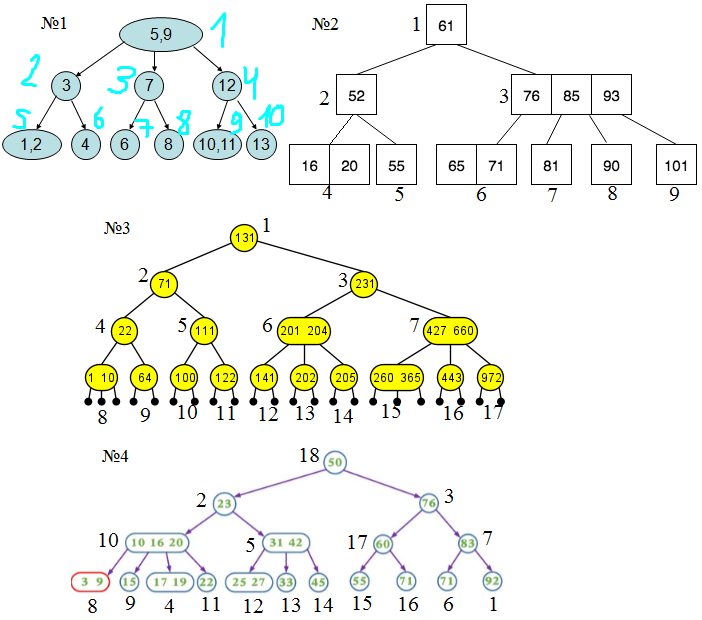
Тест №1:
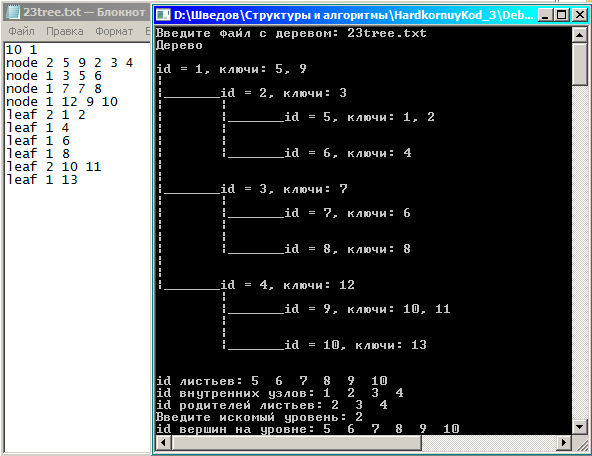
Тест №2:
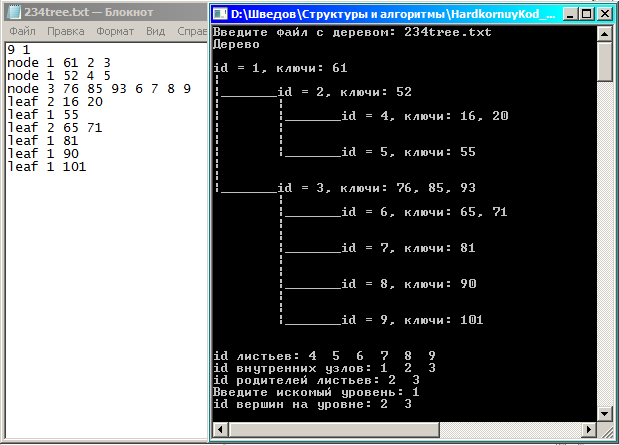
Тест №3:
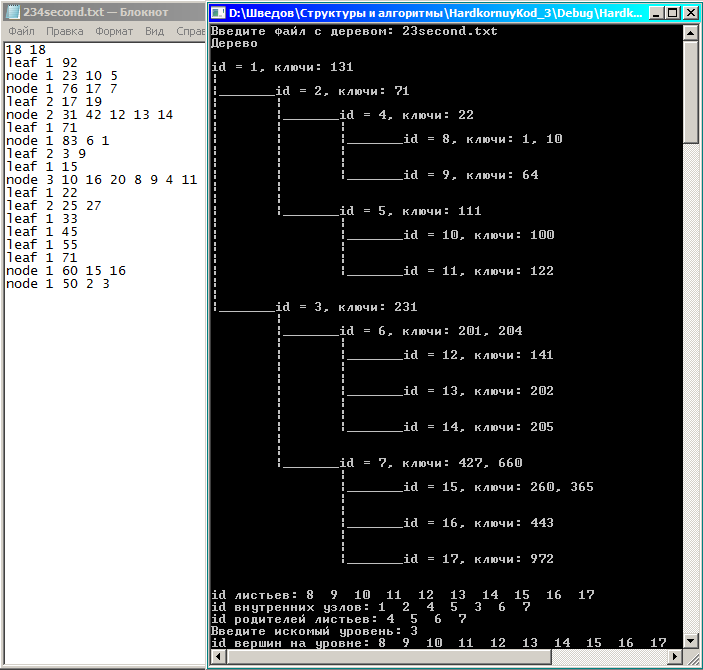
Тест №4:
4. ЛАБОРАТОРНАЯ РАБОТА №4
4.1. Задание
Имеется множество слов, т.е. строк, состоящих из букв а-я. Суммарная длина слов равна N. Алгоритмы сортировки с какой минимальной сложностью можно применить здесь? Написать программы, реализующие этот алгоритм, сравнить эффективность на примере другого метода.
4.2. Решение
Поскольку в общем случае все символы в каждой строке могут участвовать в сравнении с символами других строк, с которыми она сравнивается, и нельзя полагать, что значительная часть символов строк окажется незадействованной при сравнениях, то слова с суммарной длиной N в худшем случае нельзя отсортировать быстрее, чем за время O(N).
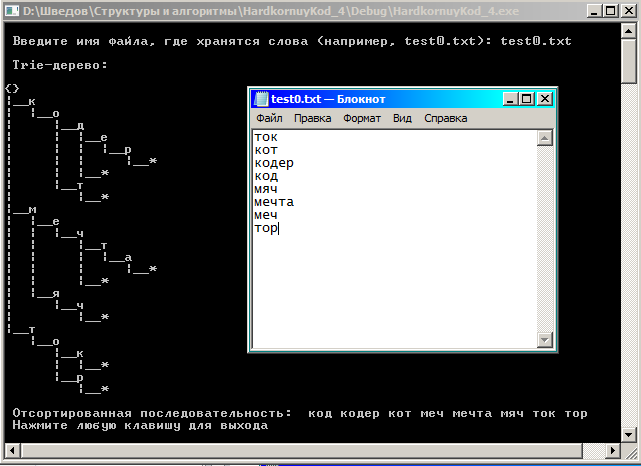
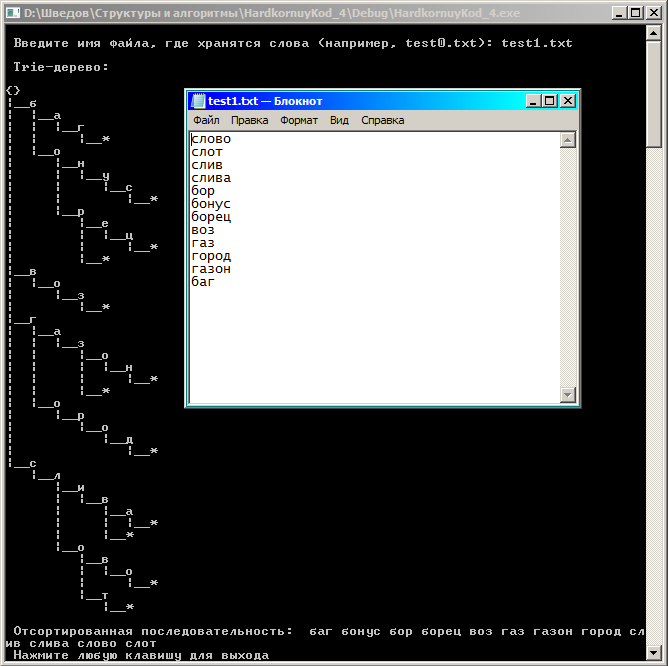
Пример алгоритма минимального порядка сложности (далее реализуется именно он). При сортировке числовых данных используется такой алгоритм, как сортировка вставками в дерево. Нечто аналогичное реализуем для строк, но нам нужно подходящее именно для строк (т.е. не бинарное дерево поиска и не АВЛ-дерево). Это Trie-дерево. Все сортируемые строки добавляем в Trie-дерево, и дальше обходим Trie-дерево. Чтобы можно было хранить пары строк вида (W, W+Z), расширяем алфавит символом конца ввода, и тогда одно слово может быть началом другого. Время добавления строки длиной L составляет O(L), то есть дерево строится за время O(N). Обход дерева также выполняется за время O(N), поскольку оценка количества узлов составляет O(N).
Преимущество над «быстрой сортировкой». Интерес представляет сравнение предложенной сортировки с сортировками, выполняемыми на основе массивов. Пусть n – количество слов. С ростом n отношение N/n становится стабильным (на основе аксиом теории вероятностей: средняя длина большого числа слов – показатель стабильный). Соответственно, попытки применить универсальные сортировки вроде «быстрой» сортировки при больших N и n характеризуются сложностью O(N log N), то есть при больших N «быстрая сортировка» уступит сортировке вставками в Trie-дерево. При небольших N и n сортировка вставками в Trie-дерево невыгодна, потому что хотя операций немного, они довольно сложны. Например, довольно дорогостоящей является операция выделения памяти под узел с последующей инициализацией указателей в узле. Обход дерева также намного дороже, чем простой вывод на экран содержимого строкового массива.
#include
#include
#include
#include
#include
#include
#define ALPH_CARD 32 /* количество символов в алфавите */
#define MAXWORDSZ 21 /* максимальный размер слова минус 1 */
using namespace std;
struct Node /* структура УЗЕЛ ДЕРЕВА */
{
Node * next[ALPH_CARD + 1]; /* указатели на потомков */
Node(); /* конструктор */
bool IsLeaf(); /* является ли узел листом? */
int FindLastChild(); /* находим номер самого правого сына */
};
Node::Node()
{
for (int i = 0; i < ALPH_CARD + 1; i++)
{
this->next[i] = NULL; /* потомков пока что нет */
}
}
bool Node::IsLeaf()
{
for (int i = 0; i < ALPH_CARD + 1; i++)
if (this->next[i] != NULL) return false;
return true;
}
int Node::FindLastChild()
{
for (int i = ALPH_CARD; i >= 0; i--)
if (this->next[i] != NULL) return i;
return -1;
}
class TrieDerevo /* класс trie-дерево */
{
private:
int pos; /* вспомогательное поле для подсчёта при поиске */
Node *root; /* указатель на корень */
char AlphStart; /* первый символ алфавита */
int NumInAlph(char c) { return c - AlphStart; } /* определение, каким по счёту в алфавите заданный символ */
void Print(Node *rt, int level, int num_of_child, bool Vis[]); /* вывод поддерева на экран */
void Add(char *word); /* добавление слова */
void DelTree(Node *rt); /* удаление поддерева */
// вывод строк в порядке их возрастания - вспомогательная функция
void PrintContent(Node * rt, char prefix[], int level);
public:
TrieDerevo(char c) { root = new Node; AlphStart = c; } /* конструктор */
bool AddFromFile(char *FileName); /* добавление коллекции из файла */
void Print() { bool Vis[1]; Print(root, 0, -1, Vis); } /* вывод всего дерева на экран */
// вывод строк в порядке их возрастания - основная функция
void PrintContent() { this->PrintContent(this->root, "", 0); }
TrieDerevo() { DelTree(root); } /* деструктор */
#include
#include
#include
#include
#include
#define ALPH_CARD 32 /* количество символов в алфавите */
#define MAXWORDSZ 21 /* максимальный размер слова минус 1 */
using namespace std;
struct Node /* структура УЗЕЛ ДЕРЕВА */
{
Node * next[ALPH_CARD + 1]; /* указатели на потомков */
Node(); /* конструктор */
bool IsLeaf(); /* является ли узел листом? */
int FindLastChild(); /* находим номер самого правого сына */
};
Node::Node()
{
for (int i = 0; i < ALPH_CARD + 1; i++)
{
this->next[i] = NULL; /* потомков пока что нет */
}
}
bool Node::IsLeaf()
{
for (int i = 0; i < ALPH_CARD + 1; i++)
if (this->next[i] != NULL) return false;
return true;
}
int Node::FindLastChild()
{
for (int i = ALPH_CARD; i >= 0; i--)
if (this->next[i] != NULL) return i;
return -1;
}
class TrieDerevo /* класс trie-дерево */
{
private:
int pos; /* вспомогательное поле для подсчёта при поиске */
Node *root; /* указатель на корень */
char AlphStart; /* первый символ алфавита */
int NumInAlph(char c) { return c - AlphStart; } /* определение, каким по счёту в алфавите заданный символ */
void Print(Node *rt, int level, int num_of_child, bool Vis[]); /* вывод поддерева на экран */
void Add(char *word); /* добавление слова */
void DelTree(Node *rt); /* удаление поддерева */
// вывод строк в порядке их возрастания - вспомогательная функция
void PrintContent(Node * rt, char prefix[], int level);
public:
TrieDerevo(char c) { root = new Node; AlphStart = c; } /* конструктор */
bool AddFromFile(char *FileName); /* добавление коллекции из файла */
void Print() { bool Vis[1]; Print(root, 0, -1, Vis); } /* вывод всего дерева на экран */
// вывод строк в порядке их возрастания - основная функция
void PrintContent() { this->PrintContent(this->root, "", 0); }
};
// вывод строк в порядке их возрастания - вспомогательная функция
void TrieDerevo::PrintContent(Node * rt, char prefix[], int level)
{
/* если у узла есть потомок, соответствующий символу
конца ввода, то префикс узла является одним из хранящихся слов */
if (rt->next[ALPH_CARD] != NULL)
cout << " " << prefix;
// проверка для всех указателей на потомков узла rt
for (int i = 0; i < ALPH_CARD; i++)
{
// если имеется потомок, соответствующий i-ом символу алфавита
if (rt->next[i] != NULL)
{
// запоминаем префикс потомка
char tmp[MAXWORDSZ];
strncpy_s(tmp, prefix, level);
tmp[level] = (char(this->AlphStart + i));
tmp[level + 1] = 0;
// рекурсивно вызываем функцию для потомка
PrintContent(rt->next[i], tmp, level + 1);
}
}
}
void TrieDerevo::Add(char *word) // добавление слова в Trie-дерево
{
Node * cur = root; /* спуск начинаем с корня */
int n = strlen(word), pos, cur_symb = 0; /* cur_symb – какой символ вставляемого слова сейчас актуален */
while (1) // цикл спуска по дереву
{
pos = NumInAlph(word[cur_symb]); /* ищем, каким по счёту а алфавите актуальный символ */
if (cur_symb == n) /* если актуальный символ - последний в слове */
{
cur->next[ALPH_CARD] = new Node;
return;
}
/* если актуальный символ - не последний в слове */
if (cur->next[pos] == NULL) /* если у текущего узла нет потомка, соответствующего актуальному символу */
{
/* создаём такого потомка */
Node * child = new Node;
cur->next[pos] = child;
}
cur = cur->next[pos]; /* спускаемся на следующий уровень дерева */
cur_symb++; /* запоминаем, что ещё один символ добавляемого слова использован */
}
}
// загружаем в дерево коллекцию из файла
bool TrieDerevo::AddFromFile(char *FileName)
{
/* пытаемся открыть файл */
ifstream f(FileName, ios::in);
if (!f) return false; /* если это не удаётся, возвращаем неуспех */
char cur_word[100];
this->root = new Node;
while (!f.eof()) /* пока не пройдём весь файл */
{
f >> cur_word; /* считываем слово */
this->Add(cur_word); /* добавляем его в дерево */
}
f.close();
return true;
}
// вывод поддерева на экран
void TrieDerevo::Print(Node *rt, int level, int num_of_child, bool Vis[])
{
if (level > 0) // выводим отступа
{
for (int i = 0; i < level - 1; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
if (level > 0) cout << "|__";
}
if (level == 0) cout << "{}\n";
else
{
// выводим символ, соответствующий узлу
if (rt->IsLeaf() == false)
cout << char(this->AlphStart + num_of_child) << "\n";
else cout << "*\n";
}
if (rt->IsLeaf() == true) return;
int lchild = rt->FindLastChild();
// рекурсивно вызываем функцию для потомков
for (int i = 0; i < ALPH_CARD + 1; i++)
{
bool Temp[MAXWORDSZ];
if (level > 0)
copy(Vis, Vis + level, Temp);
Temp[level] = (i != lchild) ? true : false;
if (rt->next[i] != NULL)
Print(rt->next[i], level + 1, i, Temp);
}
}
// удаление поддерева
void TrieDerevo::DelTree(Node *rt)
{
if (!rt) return;
/* сначала удаляем потомков узла */
for (int i = 0; i < ALPH_CARD; i++)
if (rt->next[i]) DelTree(rt->next[i]);
delete rt; /* затем сам узел */
}
void main()
{
setlocale(LC_ALL, "rus");
char FileName[MAXWORDSZ];
cout << "\n Введите имя файла, где хранятся слова (например, test0.txt): ";
// пользователь вводит имя файла с неотсортированной коллекцией
cin >> FileName;
TrieDerevo T('а');
// не исключено, что файл не существует
if (T.AddFromFile(FileName) == false)
cout << "\n Файл не найден";
// если файл существует
else
{
cout << "\n Trie-дерево:\n\n";
// показываем построенное Trie-дерево
T.Print();
cout << "\n Отсортированная последовательность: ";
// на основе обхода Trie-дерева показываем отсортированную коллекцию слов
T.PrintContent();
}
cout << "\n Нажмите любую клавишу для выхода";
_getch();
}
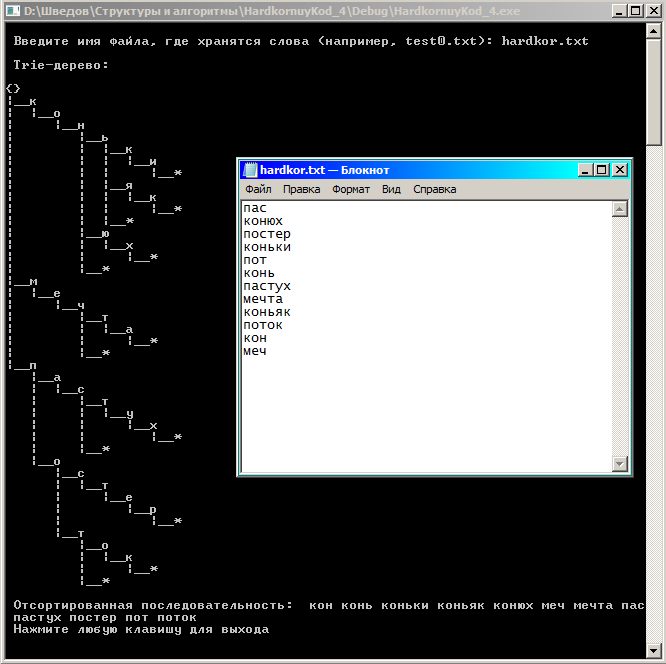
4.3. Демонстрация программы
Самый сложный из тестов, с высокой вероятностью проявляющий «баги», если есть цепочка ситуаций, когда одно слово – начало другого. Далее «кон» – начало «конь» и «конюх», а «конь» – начало «коньяк» и «коньки» (имеем цепочку отношений «одно слово – начало другого»). Программа успешно прошла и такой запутанный тест.
5. ЛАБОРАТОРНАЯ РАБОТА №5
5.1. Задание
Составить программу поиска записи с включением в сбалансированном бинарном дереве поиска (АВЛ-дереве).
5.2. Решение
Поиск с включением в АВЛ-дерево осуществляется следующим образом. 1. Сначала ведем спуск по дереву, как для обычного бинарного дерева поиска. Выбираем правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. 2. При вставке ключа требуется проверить, не нарушены ли требования к показателю сбалансированности. В случае необходимости выполняется балансировка.
Также дадим краткое пояснение визуализации дерева «с веточками» в консольном приложении (PrintTree ниже). Требуется использовать для каждого узла уровень и булев массив, который задает, где нужно выводить вертикальные полосы (символ «|») на текущей строке консольного окна (true – выводить полосу по соответствующей позиции, false – нет). 1. Выводим содержимое, предшествующее в строке содержимому корня поддерева (включая полосы). 2. Выводим корень. 3. Рекурсия для поддеревьев.
#include
#include
#include
#include
#include
#include
using namespace std;
// белый цвет текста
int white_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_RED | FOREGROUND_INTENSITY;
// голубой цвет текста
int cyan_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_INTENSITY;
// получаем дескриптор для устройства вывода
HANDLE handle = GetStdHandle(STD_OUTPUT_HANDLE);
void SetColor(int color)
{
// установка цвета текста
SetConsoleTextAttribute(handle, color);
}
struct node // структура для представления узлов АВЛ-дерева
{
int item; // элемент
unsigned char height; // высота поддерева с корнем в данном узле
node * left, *right; // указатели на левое и правое поддеревья
node(int item) // конструктор
{
this->item = item;
left = right = 0;
height = 1;
}
};
class Avlka
{
private:
node *Root; // корень дерева
// для запоминания, найден ли такой ключ,
// при попытке добавить ключ
bool HasFound;
/* Вспомогательные функции, связанные с высотой
height она может работать с нулевыми указателями(с пустыми деревьями);
bfactor вычисляет показатель сбалансированности для узла(и работает только с ненулевыми указателями);
fixheight восстанавливает корректное значение поля height заданного узла
(при условии, что значения этого поля в правом и левом дочерних узлах являются корректными) * /
*/
unsigned char height(node* p)
{
return p ? p->height : 0;
}
int bfactor(node* p)
{
// показатель сбалансированности поддерева с корнем p
return height(p->right) - height(p->left);
}
void fixheight(node* p)
{
unsigned char hl = height(p->left);
unsigned char hr = height(p->right);
p->height = (hl>hr ? hl : hr) + 1;
}
node* rotateright(node* p); // правый поворот вокруг p
node* rotateleft(node* q); // левый поворот вокруг q
node* balance(node* p); // балансировка узла p
node* Vstavka(node* p, int item); // вставка в дерево с корнем p
// вывод поддерева на экран
void PrintTree(node * rt, int level, int num_of_child, bool Vis[]);
void DelTree(node * root); // удаление дерева
public:
// конструктор с построением по заданной
// последовательности
Avlka(int A[], int n)
{
Root = NULL;
for (int i = 0; i < n; i++)
Vstavka(A[i]);
}
void PrintTree() // вывод дерева
{
bool Vis[1];
PrintTree(Root, 0, -1, Vis);
}
bool Vstavka(int item) // добавление отдельного элемента
{
HasFound = false;
Root = Vstavka(Root, item);
// вставка считается неуспешной, если item
// уже был в дереве
return !HasFound;
}
Avlka() { DelTree(Root); }
#include
#include
#include
#include
#include
using namespace std;
// белый цвет текста
int white_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_RED | FOREGROUND_INTENSITY;
// голубой цвет текста
int cyan_color = FOREGROUND_BLUE | FOREGROUND_GREEN | FOREGROUND_INTENSITY;
// получаем дескриптор для устройства вывода
HANDLE handle = GetStdHandle(STD_OUTPUT_HANDLE);
void SetColor(int color)
{
// установка цвета текста
SetConsoleTextAttribute(handle, color);
}
struct node // структура для представления узлов АВЛ-дерева
{
int item; // элемент
unsigned char height; // высота поддерева с корнем в данном узле
node * left, *right; // указатели на левое и правое поддеревья
node(int item) // конструктор
{
this->item = item;
left = right = 0;
height = 1;
}
};
class Avlka
{
private:
node *Root; // корень дерева
// для запоминания, найден ли такой ключ,
// при попытке добавить ключ
bool HasFound;
/* Вспомогательные функции, связанные с высотой
height она может работать с нулевыми указателями(с пустыми деревьями);
bfactor вычисляет показатель сбалансированности для узла(и работает только с ненулевыми указателями);
fixheight восстанавливает корректное значение поля height заданного узла
(при условии, что значения этого поля в правом и левом дочерних узлах являются корректными) * /
*/
unsigned char height(node* p)
{
return p ? p->height : 0;
}
int bfactor(node* p)
{
// показатель сбалансированности поддерева с корнем p
return height(p->right) - height(p->left);
}
void fixheight(node* p)
{
unsigned char hl = height(p->left);
unsigned char hr = height(p->right);
p->height = (hl>hr ? hl : hr) + 1;
}
node* rotateright(node* p); // правый поворот вокруг p
node* rotateleft(node* q); // левый поворот вокруг q
node* balance(node* p); // балансировка узла p
node* Vstavka(node* p, int item); // вставка в дерево с корнем p
// вывод поддерева на экран
void PrintTree(node * rt, int level, int num_of_child, bool Vis[]);
void DelTree(node * root); // удаление дерева
public:
// конструктор с построением по заданной
// последовательности
Avlka(int A[], int n)
{
Root = NULL;
for (int i = 0; i < n; i++)
Vstavka(A[i]);
}
void PrintTree() // вывод дерева
{
bool Vis[1];
PrintTree(Root, 0, -1, Vis);
}
bool Vstavka(int item) // добавление отдельного элемента
{
HasFound = false;
Root = Vstavka(Root, item);
// вставка считается неуспешной, если item
// уже был в дереве
return !HasFound;
}
};
node* Avlka::rotateright(node* p) // правый поворот вокруг p
{
node* q = p->left;
p->left = q->right;
q->right = p;
fixheight(p);
fixheight(q);
return q;
}
node* Avlka::rotateleft(node* q) // левый поворот вокруг q
{
node* p = q->right;
q->right = p->left;
p->left = q;
fixheight(q);
fixheight(p);
return p;
}
/* функции редактирования дерева (балансировка, вставка, удаление) */
node* Avlka::balance(node* p) // балансировка узла p
{
fixheight(p);
if (bfactor(p) == 2) // если "перекос" в сторону правого поддерева
{
if (bfactor(p->right) < 0)
p->right = rotateright(p->right);
return rotateleft(p);
}
if (bfactor(p) == -2) // если "перекос" в сторону левого поддерева
{
if (bfactor(p->left) > 0)
p->left = rotateleft(p->left);
return rotateright(p);
}
return p; // здесь окажемся, если балансировка не понадобилась
}
node* Avlka::Vstavka(node* p, int item) // вставка в дерево с корнем p
{
if (!p) return new node(item); // особый случай - если дерево пустое
if (p->item == item) // если нашли такой же ключ
{
HasFound = true; // запоминаем, что он найден
return p;
}
// вставку делаем по правилу бинарного дерева поиска
if (p->item > item)
p->left = Vstavka(p->left, item);
else
p->right = Vstavka(p->right, item);
return balance(p); /* после вставки выполняем балансировку,
если она потребуется */
}
void Avlka::DelTree(node * root) // удаление дерева
{
if (!root) return;
DelTree(root->left); // удаляем левое поддерево
DelTree(root->right); // удаляем правое поддерево
delete root; // удаляем корень
}
// вывод поддерева на экран
void Avlka::PrintTree(node * rt, int level, int num_of_child, bool Vis[])
{
if (level > 0) // выводим отступы
{
for (int i = 0; i < level - 1; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
if (level > 0) cout << "|__";
}
if (num_of_child != -1)
{
if (num_of_child == 0) cout << "L: ";
else cout << "R: ";
}
// выводим содержимое узла и показатель сбалансированности
cout << (rt->item) << ", bfactor: " << bfactor(rt) << "\n";
if (rt->left == NULL && rt->right == NULL)
{
for (int i = 0; i < level; i++)
{
if (Vis[i] == true) cout << "| ";
else cout << " ";
}
cout << "\n";
return;
}
int lchild = (rt->right != NULL) ? 1 : 0;
node * deti[] = { rt->left, rt->right };
// рекурсивно вызываем функцию для потомков
for (int i = 0; i < 2; i++)
{
bool Temp[40];
if (level > 0)
copy(Vis, Vis + level, Temp);
Temp[level] = (i != lchild) ? true : false;
if (deti[i]) PrintTree(deti[i], level + 1, i, Temp);
}
}
// создаем массив уникальных чисел рандомом
void RandomArr(int A[], int n)
{
srand(time(0)); // инициализируем случайный датчик