ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 102
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
for (int i = 0; i < n; i++)
{
// рандомное число от 1 до 1000
A[i] = rand() % 1001 + 1;
// если такой элемент уже есть
if (find(A, A + i, A[i]) != (A + i))
i--; // взаимно уничтожится с i++
}
}
void ShowArray(int A[], int n)
{
for (int i = 0; i < n; i++)
cout << " " << A[i];
cout << endl;
}
void main()
{
setlocale(LC_CTYPE, "rus");
SetColor(white_color);
int n;
cout << "Введите число случайных ключей: ";
cin >> n;
int * A = new int[n];
RandomArr(A, n); // рандомом заполняем массив
cout << "Случайный массив: ";
SetColor(cyan_color); // чтобы вывести цветом
ShowArray(A, n); // выводим массив
SetColor(white_color);
// формируем дерево по массиву ключей
Avlka MEGADEREVCE(A, n);
cout << "Авлка:\n";
SetColor(cyan_color);
MEGADEREVCE.PrintTree(); // выводим дерево
SetColor(white_color);
delete[] A;
// добавляем ключи в дерево, пока не надоест
while (true)
{
int key;
cout << "Введите добавляемый ключ (или 0 - для выхода): ";
SetColor(cyan_color);
cin >> key;
if (key == 0) break;
SetColor(white_color);
// вернет false при дублировании ключей
if (MEGADEREVCE.Vstavka(key) == false)
cout << "Такой ключ уже есть\n";
else // при недублировании ключей
{
cout << "Авлка:\n";
SetColor(cyan_color);
MEGADEREVCE.PrintTree(); // покажем обновленное дерево
SetColor(white_color);
}
}
}
5.3. Демонстрация программы
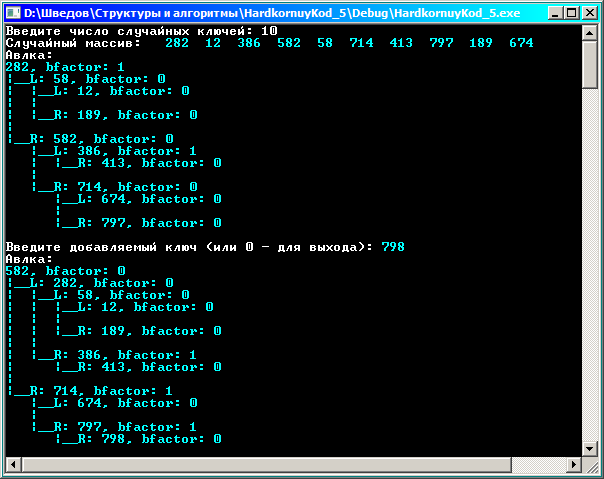
Сформируем дерево по случайным ключам.
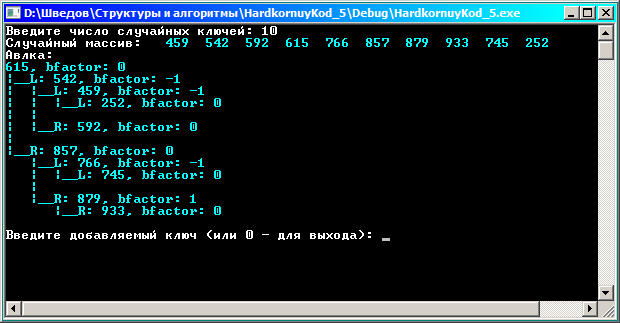
Обозначения: L - левое поддерево, R - правое поддерево, bfactor - разность высоты правого и левого поддерева (у АВЛ-дерева может быть только -1, 0 или 1).
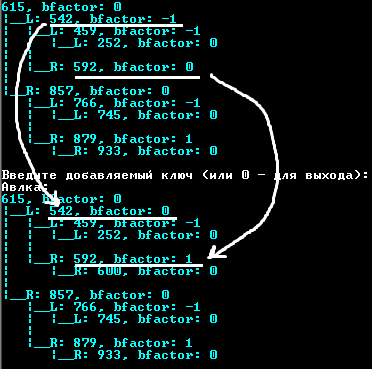
Пример вставки, когда балансировка не нужна:
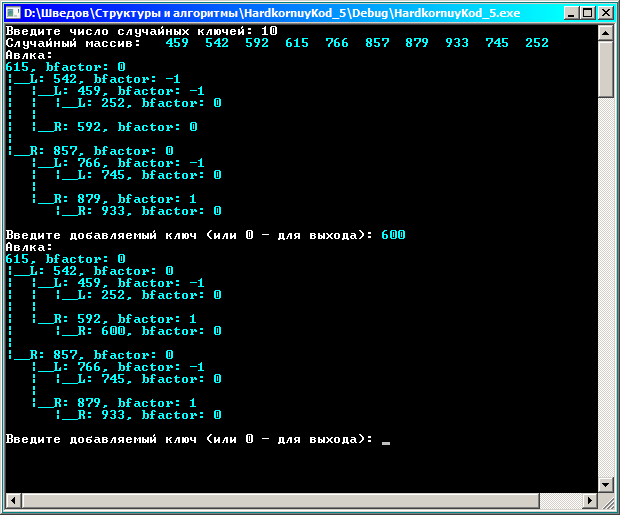
Заметим, что выполнена корректировка показателей сбалансированности.
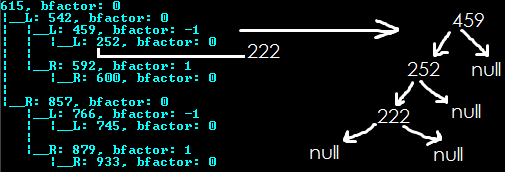
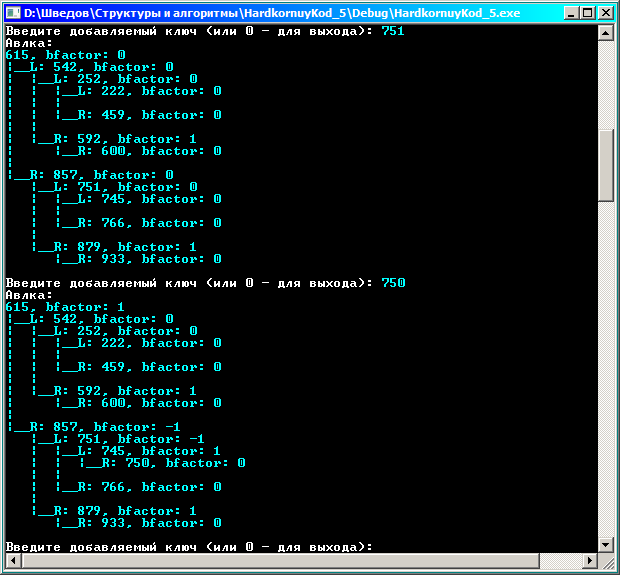
Продемонстрируем вставку для случая, когда баланс нарушится. Если вставить ключ 222 без балансировки, у поддерева с корнем 459 высота левого поддерева станет 2, а правого останется 0, т.е. показатель = -2.
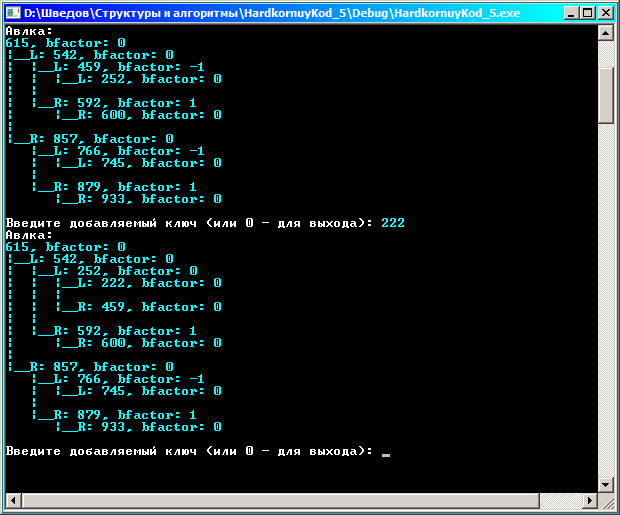
При вставке 222 программа осуществила балансировку:
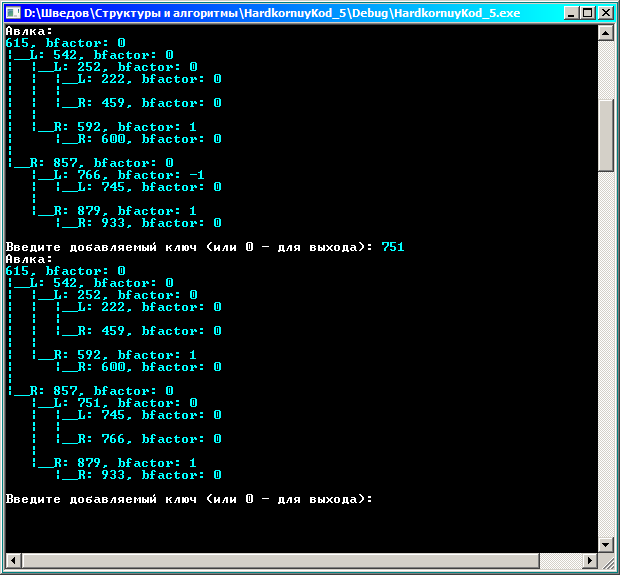
Еще несколько примеров вставки:
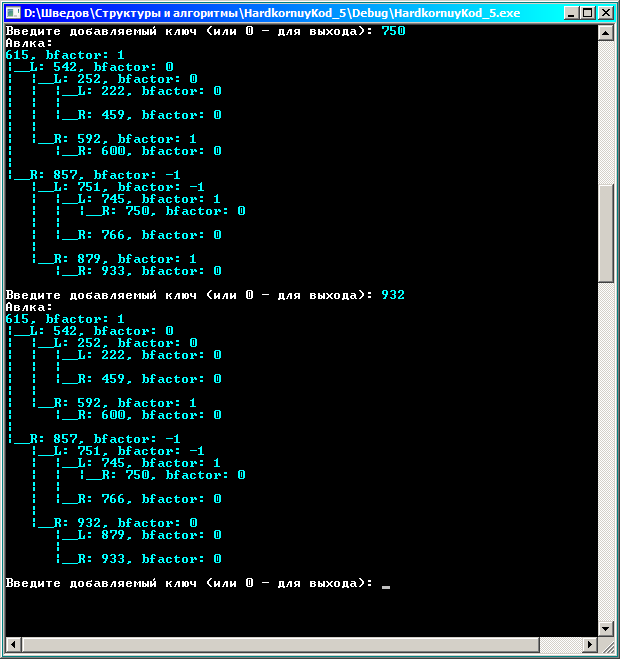
Примеры попыток добавить существующий ключ:
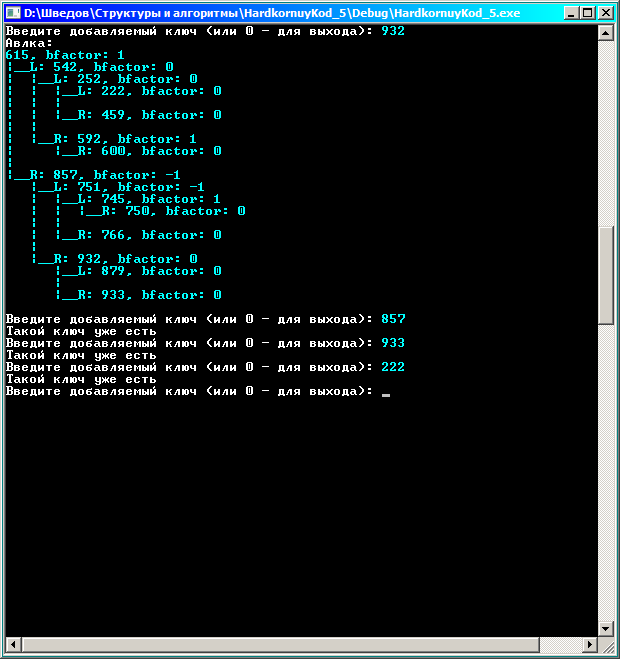
Тестирование показывает, что программа корректно работает, даже когда при вставке нарушается допустимый баланс поддеревьев корня.
6. ЛАБОРАТОРНАЯ РАБОТА №6
6.1. Задание
Написать процедуру обхода графа G (выдачи на печать всех его вершин).
6.2. Решение
Существуют два базовых варианта – обход в глубину (DFS) и в ширину (BFS). Идея DFS заключается в том, что мы двигаемся от начальной вершины в определенном направлении (по определенному пути) до тех пор, пока можем. Если далее двигаться некуда («тупик» или все доступные вершины уже посещены), то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту. BFS подразумевает посещение соседей стартовой вершины, затем посещение соседей этих соседей и т.д.
Для реализации DFS/BFS мы поддерживаем список открытых вершин – которые предстоит проверить, и массив флагов, указывающих, является ли каждая вершина посещенной. Изначально список открытых вершин содержит только начальную. Далее, для каждой вершины из списка открытых вершин выполняется раскрытие – сама вершина считается посещенной и извлекается из списка, а еще не посещенные смежные с ней вершины заносятся в список открытых. Если извлечение из списка открытых и добавление в список – с одного конца, имеем поиск в глубину (в данном случае его нерекурсивный способ), если с разных концов – в ширину. При наличии нескольких компонент связности такой обход нужно выполнить отдельно для каждой.
#include
#include
#include
#include
#define MAXN 20
#define FAIL -1
using namespace std;
// чтение матрицы смежности из файла
int ReadMatrix(char FileName[], bool A[MAXN][MAXN])
{
ifstream file(FileName, ios::in);
int n, cur;
file >> n; // читаем число вершин
// читаем матрицу
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
file >> cur;
if (cur == 0) A[i][j] = false;
else A[i][j] = true;
}
file.close();
return n;
}
// поиск первой непосещённой вершины, начиная со start-ой
int IndexOfNotVisit(bool Visited[], int start, int n)
{
for (int i = 0; i < n; i++)
if (Visited[i] == false) return i;
return FAIL;
}
void InitBoolArr(bool Arr[], int n)
{
for (int i = 0; i < n; i++)
Arr[i] = false;
}
struct Node // узел списка вершин
{
int item; // номер вершины
Node * next; // указатель на следующий элемент
Node(int item)
{
this->item = item;
this->next = NULL;
}
};
class List // список
{
Node * head, *tail;
public:
List() { head = NULL; }
// ToHead = true - вставка в голову,
// ToHead = false - вставка в хвост
void Add(int item, bool ToHead)
{
if (head == NULL) // если список пустой
{
head = new Node(item);
// единственный узел одновременно и голова, и хвост списка
tail = head;
return;
}
if (ToHead == true)
{
Node * p = new Node(item);
p->next = head;
head = p;
}
else
{
tail->next = new Node(item);
tail = tail->next;
}
}
// извлечение содержимого головы (с удалением головы)
int ExtractHead()
{
if (head == NULL) return FAIL;
Node * q = head->next;
int extracted = head->item; // запомнить, что было в голове
delete head; // удалить голову
head = q; // кто был следующим за головой теперь голова
return extracted;
}
bool Contains(int item) // поиск элемента item
{
Node * cur = head;
while (cur)
{
if (cur->item == item) return true;
cur = cur->next;
}
return false;
}
List()
#include
#include
#include
#define MAXN 20
#define FAIL -1
using namespace std;
// чтение матрицы смежности из файла
int ReadMatrix(char FileName[], bool A[MAXN][MAXN])
{
ifstream file(FileName, ios::in);
int n, cur;
file >> n; // читаем число вершин
// читаем матрицу
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
file >> cur;
if (cur == 0) A[i][j] = false;
else A[i][j] = true;
}
file.close();
return n;
}
// поиск первой непосещённой вершины, начиная со start-ой
int IndexOfNotVisit(bool Visited[], int start, int n)
{
for (int i = 0; i < n; i++)
if (Visited[i] == false) return i;
return FAIL;
}
void InitBoolArr(bool Arr[], int n)
{
for (int i = 0; i < n; i++)
Arr[i] = false;
}
struct Node // узел списка вершин
{
int item; // номер вершины
Node * next; // указатель на следующий элемент
Node(int item)
{
this->item = item;
this->next = NULL;
}
};
class List // список
{
Node * head, *tail;
public:
List() { head = NULL; }
// ToHead = true - вставка в голову,
// ToHead = false - вставка в хвост
void Add(int item, bool ToHead)
{
if (head == NULL) // если список пустой
{
head = new Node(item);
// единственный узел одновременно и голова, и хвост списка
tail = head;
return;
}
if (ToHead == true)
{
Node * p = new Node(item);
p->next = head;
head = p;
}
else
{
tail->next = new Node(item);
tail = tail->next;
}
}
// извлечение содержимого головы (с удалением головы)
int ExtractHead()
{
if (head == NULL) return FAIL;
Node * q = head->next;
int extracted = head->item; // запомнить, что было в голове
delete head; // удалить голову
head = q; // кто был следующим за головой теперь голова
return extracted;
}
bool Contains(int item) // поиск элемента item
{
Node * cur = head;
while (cur)
{
if (cur->item == item) return true;
cur = cur->next;
}
return false;
}
{
Node * p = head, *q;
while (p)
{
q = p->next;
delete p;
p = q;
}
}
friend ostream & operator << (ostream & os, List & spisok);
};
ostream & operator << (ostream & os, List & spisok)
{
Node * cur = spisok.head;
while (cur)
{
os << (cur->item + 1) << " ";
cur = cur->next;
}
return os;
}
// процедура раскрытия вершины node
void Discover(List * Opened, bool A[MAXN][MAXN], int n, int node, bool IsDepth, bool Visited[])
{
// цикл по node-ой строке матрицы смежности
for (int k = 0; k < n; k++)
{
int i = (IsDepth == false) ? k : (n - k - 1);
// если есть связь (node, i)
if (A[node][i] == true)
{
// если i-ая вершина не посещена и отсутствует
// в списке открытых
if (Visited[i] == false && Opened->Contains(i) == false)
{
// вносим вершину в список открытых (для поиска в глубину - в голову списка, для поиска в ширину - в хвост)
Opened->Add(i, IsDepth);
}
}
}
}
// обход компоненты связности
void Traverse(bool A[MAXN][MAXN], int n, bool IsDepth, int start, bool Visited[], List * results)
{
List Opened; // открытые вершины
// вносим стартовую вершину в открытые
Opened.Add(start, IsDepth);
while (1)
{
// извлекаем головной элемент из списка открытых
int node = Opened.ExtractHead();
// если оказалось, что список открытых вершин пустой
if (node == FAIL) break;
// добавляем извлеченный элемент в список результатов
results->Add(node, false);
// помечаем node как посещённую
Visited[node] = true;
// используем процедуру раскрытия для node
Discover(&Opened, A, n, node, IsDepth, Visited);
}
}
// основная функция обхода
List * Traverse(bool A[MAXN][MAXN], int n, bool IsDepth)
{
List * results = new List;
// создаем массив для хранения информации о том, какие вершины посещали
bool Visited[MAXN];
// пока что заполняем его значениями false
InitBoolArr(Visited, n);
int node = 0;
// цикл вызовов вспомогательной функции -
// свой вызов на каждую компоненту связности
while (node != FAIL)
{
Traverse(A, n, IsDepth, node, Visited, results);
// проверим, все ли вершины посещены, и выдадим индекс
// первой не посещённой (если такие ещё есть)
node = IndexOfNotVisit(Visited, node + 1, n);
}
return results;
}
void main()
{
setlocale(LC_ALL, "rus");
bool A[MAXN][MAXN];
char FileName[30];
cout << "Введите имя файла: ";
cin >> FileName;
int n = ReadMatrix(FileName, A);
List * spisok = Traverse(A, n, true);
cout << "Обход в глубину: " << (*spisok) << "\n";
delete spisok;
spisok = Traverse(A, n, false);
cout << "Обход в ширину: " << (*spisok) << "\n";
delete spisok;
_getch();
}
6.3. Демонстрация программы
Тест для дерева:
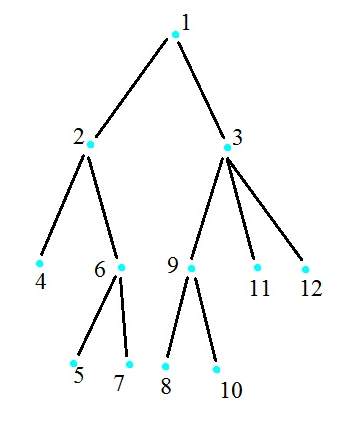
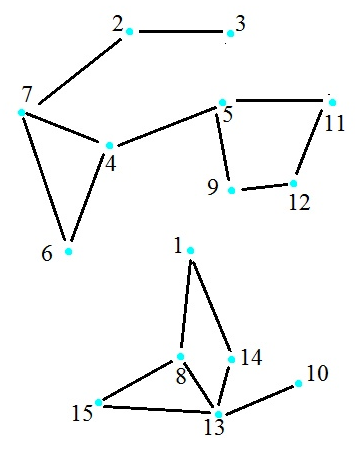
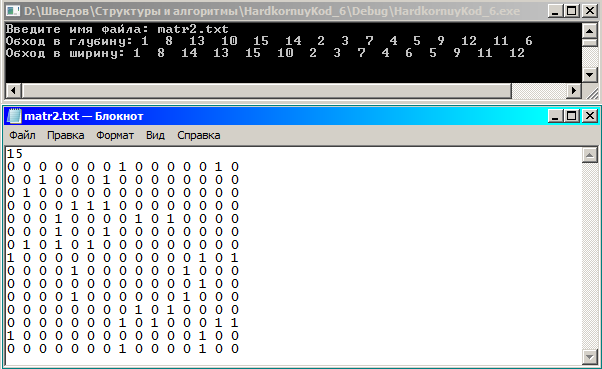
Вид матрицы смежности в файле и самой программы:
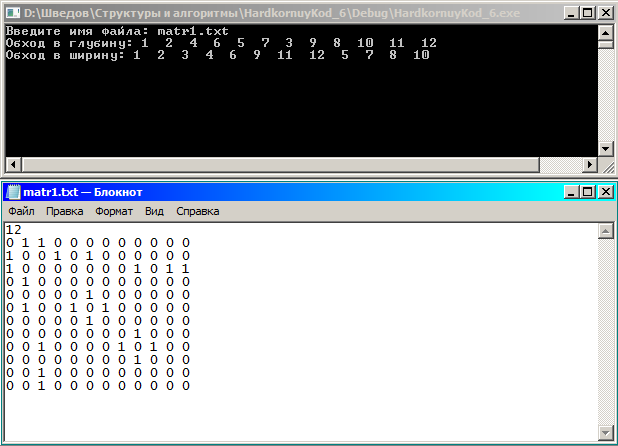
Тест для графа с двумя компонентами связности, каждая из которых содержит циклы (тем самым мы проверяем, правильно ли учитываются флаги посещения вершин в функции раскрытия):