Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл (3,25Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 141

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

_{МИНОБРНАУКИ} РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования

«Тульский государственный университет» Институт прикладной математики и компьютерных наук

Утверждено на заседании совета Института прикладной

математики и компьютерных наук

« 24 » июня 2022 г., протокол № 10

Директор ИПМиКН

А.А. Сычугов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению курсовой работы по дисциплине (модулю)

«Введение в математический анализ»

основной профессиональной образовательной программы высшего образования – программы бакалавриата
01.00.00 Математика и механика

09.00.00 Информатика и вычислительная техника

10.00.00 Информационная безопасность Форма обучения: очная

Тула 2023 год

Разработчики методических указаний

Боницкая О.В., к.ф.-м.н.

Инченко О.В., к.ф.-м.н.

Кузнецова В.А., к.ф.-м.н.

(подпись)(подпись)(подпись)

ВВЕДЕНИЕ

Цель выполнения курсовой работы в рамках дисциплины «Введение в математический анализ» - углубленное изучение теоретического материала и отработка практических навыков применения методов качественного исследования и программных пакетов при вычислении определенных и несобственных интегралов.

Основное требование к курсовой работе – умение

сочетать классические качественные методы исследования и вычисления определенных и несобственных интегралов с современными численно- аналитическими методами их исследования и вычисления, предполагающими использование стандартных функций, заложенных в математическом пакете wxMaxima.

Исходные данные заданий курсовой работы содержатся в данных методических указаниях. Данные по каждому разделу курсовой работы предваряются формулировкой заданий, необходимым теоретическим материалом для их выполнения, а также рекомендациями и примерами выполнения аналогичных заданий.

Курсовая работа предусматривает выполнение заданий, тематика которых сформулирована непосредственно в тексте данных методических указаний. Объем курсовой работы не регламентируется и может варьироваться в зависимости от конкретного варианта задания.

Курсовая работа выполняется в течение 2-го семестра обучения.

Защита курсовой работы проходит в форме индивидуальной беседы с преподавателем в период с 14 по 16 неделю учебного семестра включительно. Перед защитой необходимо получить оценку рецензента.

Оформление курсовой работы осуществляется согласно требованиям, содержащимся в данных методических указаниях.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Тульский государственный университет»

Институт прикладной математики и компьютерных наук

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту по курсу

«ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ»

на тему

«Приближенные методы вычисления интегралов»

Автор работыстудент гр.

(дата, подпись) (фамилия и инициалы)
Руководитель работы

(дата, подпись) (должность) (фамилия и инициалы)

Работа защищенас оценкой

(дата)

Члены комиссии

(дата, подпись) (должность) (фамилия и инициалы)

(дата, подпись) (должность) (фамилия и инициалы)

(дата, подпись) (должность) (фамилия и инициалы)

Тула 2023

ЗАДАНИЕ

на курсовой проект по дисциплине

«ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ»

студенту гр.

(фамилия, имя, отчество)

Тема работы: «Приближенные методы вычисления интегралов» Входные данные: (формулировка всех заданий варианта)

Задание получил

(подпись) (дата)

График выполнения работы:
Замечания консультанта

К защите. Руководитель работы

(подпись) (дата)

Приложение определенных интегралов.

Площадь плоской фигуры

Если

f(x)  0

^на[a,b] ^,^то^{интеграл}

b

_f_x_dx

a

геометрически представляет

собой площадькриволинейнойтрапеции,которая ограничена графиком

функции

^y^^f⁽^x⁾, прямыми x a, x bи осью Ox, т.е.

b

S _f_x_dx

a

Пусть криволинейная трапеция ограничена слева и справа прямыми x a,

x b, сверху - графиком функции f_x_, снизу - графиком функции g_x_.

b

Тогда площадь фигуры, ограниченной данными линиями вычислим по формуле:

S __f_x_ g_x__dx.

a
Пример 1. Вычислить площадь фигуры, ограниченной линиями:

1) y x²  2x 4 ,

y 3,

x 1

Построим графики данных функций. Найдем точку пересечения прямой
y 3
и параболы
y x²  2x 4 . Для

этого приравняем значения y: 3  x²  2x 4 . Отсюда получаем

^x²^²^x^¹^⁰^, ^x^¹2 ^⁰^,

x1. При

этом Если

y 3.

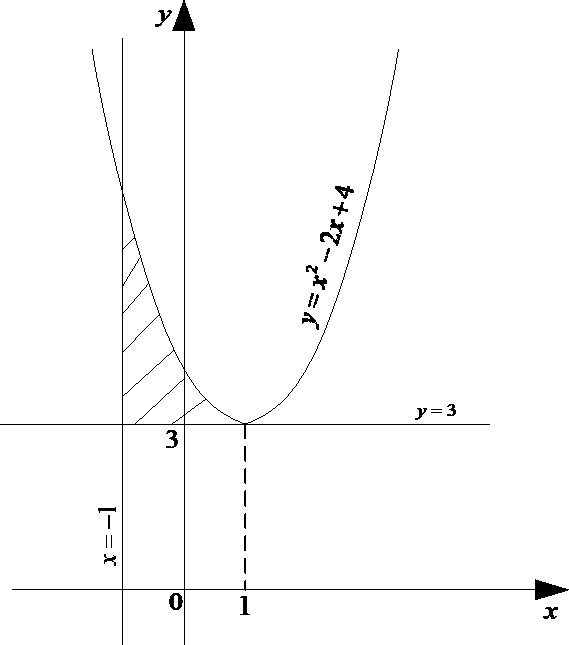x 1, то

y (1)²  2  (1)  4  7 .

Найдем вершину параболы:

x ^^b ² 1, y_1_ 3- это точка

2a 2

пересечения прямой и параболы. Строим область, площадь которой надо вычислить:

b

Тогда площадь фигуры, ограниченной данными линиями вычислим по формуле:

^S^__^f ^x ^^g ^x_^dx,

a