Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 143
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
y sin x,
2
y 2 ,
x 0,
x 2 .
Построим чертеж.
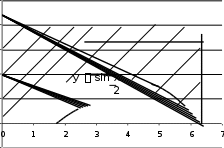 2,5
2,52
x 2
1,5
1
0,5
0
-0,5
2 2
2
x
x2
S 2 sin dx 2x 2cos
0 0
4 2 2 4 4 ,
т.е. S 4 4ед2 .
3) y 2x2 8x 4 , y x2 x 4 .
y 2x2 8x 4 - парабола, ветви направлены вверх, y x2 x 4 -
парабола, ветви направлены вниз. Значит, фигура ограниченна сверху
параболой
y x2 x 4 , а снизу параболой
y=2x2 8x 4 .
Найдем точки пересечения линий:
2x2 8x 4 x2 x 4 ,
3x2 9x 0 ,
3x x 3 0 ,
откуда
x1 0 ,
x2 3.
Вычислим значения ординат: при
x1 0
получаем
y1 4 , при
x2 3
получаем
y2 2 .
Построим графики парабол и найдем область, площадь которой надо вычислить:
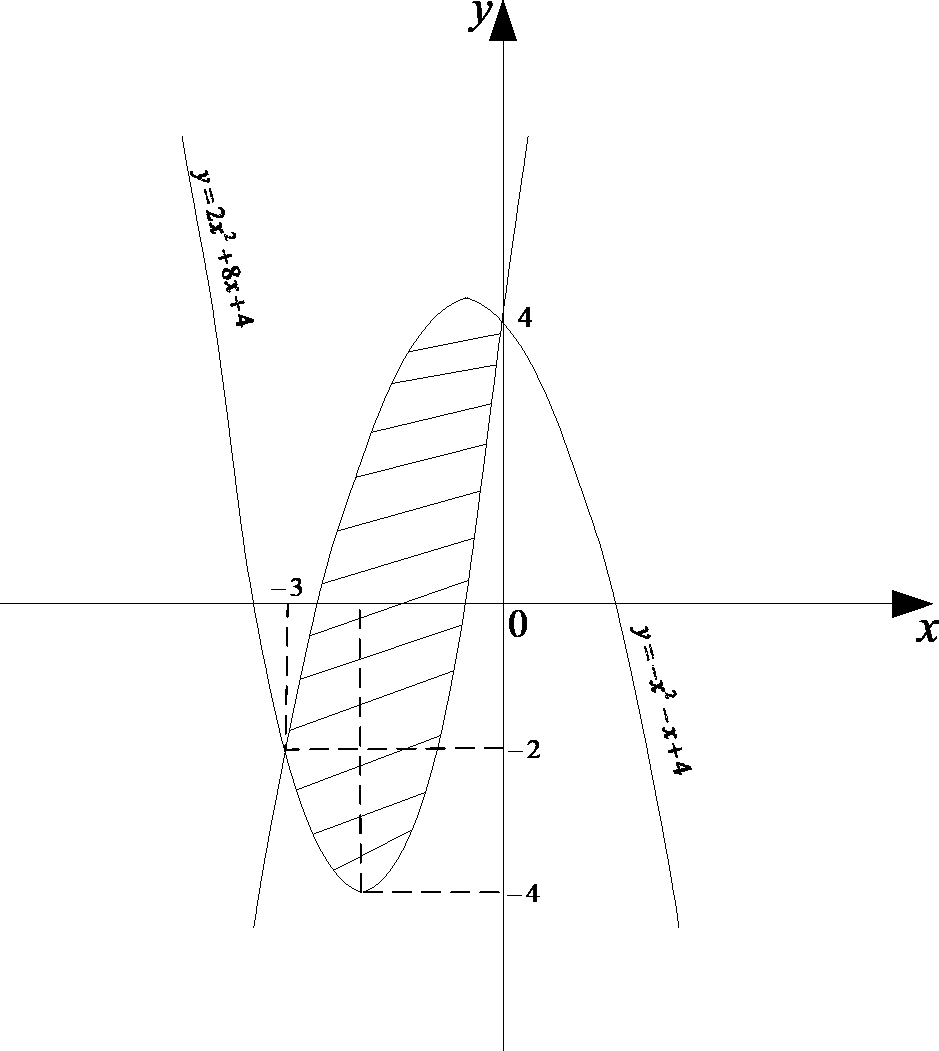
Найдем площадь фигуры:
0 0
9 0
S x2 x 4 2x2 8x 4dx 3x2 9xdx x3
x2
3 3
2 3


0 27 81 27 ,
2 2
т.е.
2
S 27 ед2 .
Для решения подобных задач в Maxima следует выполнить следующиедействия:
-
Изобразить кривые, которые задают рассматриваемый объект. -
Найти точки пересечения этих кривых. -
При необходимости разбить фигуру на области. -
Вычислить определенные интегралы с помощью программы Maxi- ma и вручную. -
Записать ответ.
Пример 2. Вычислить площадь фигуры, ограниченной следующими линиями
y 3x x2 и y x2 x.
Зададим
функции и построим графики:
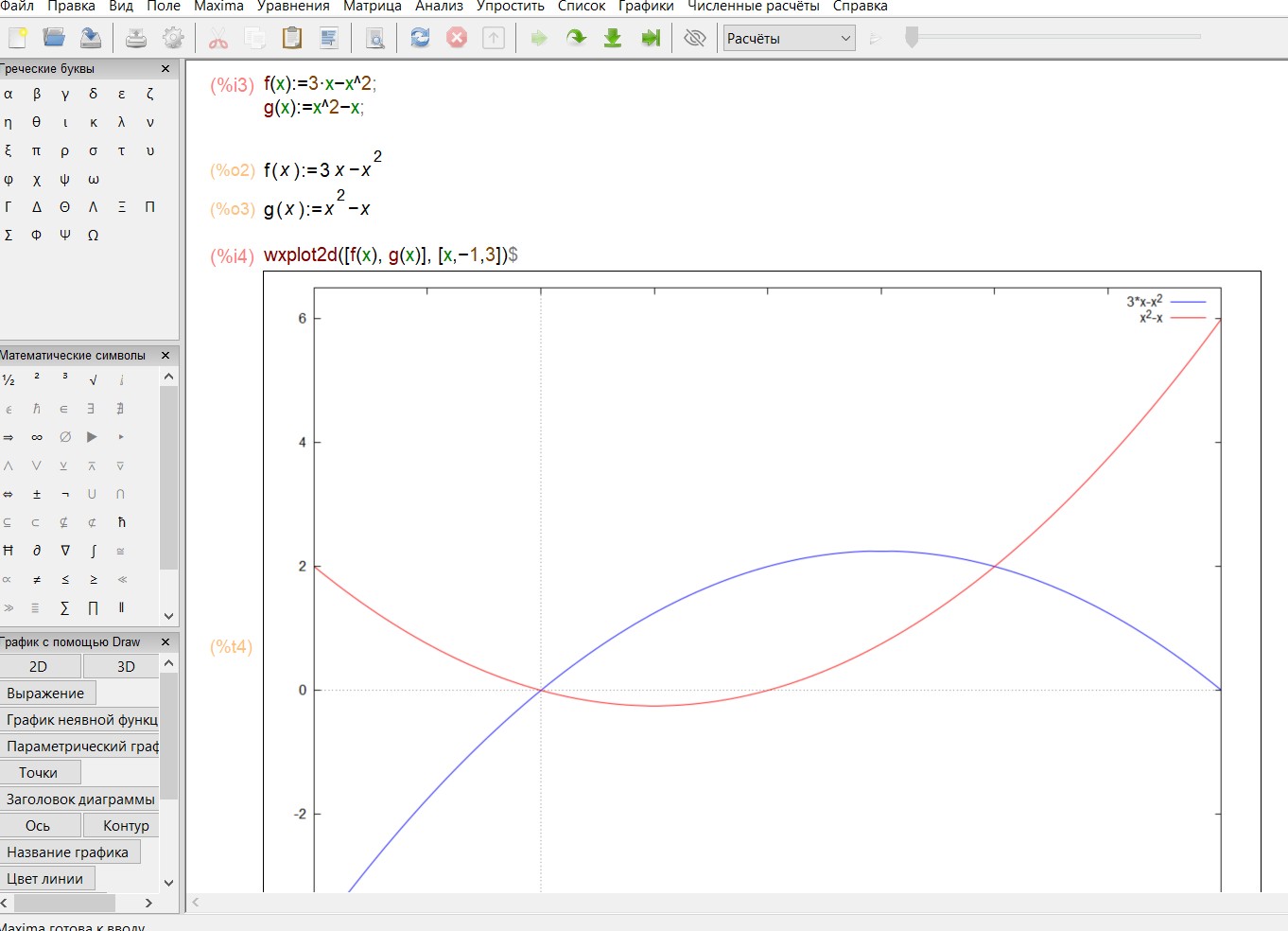
Из графика видно, что функции пересекаются в двух точках, и об- ласть является простой, т.е. ее не нужно делить на подобласти.
Найдем точки пересечения кривых, затем составим и вычислим определен- ный интеграл, результат которого и есть площадь данной фигуры
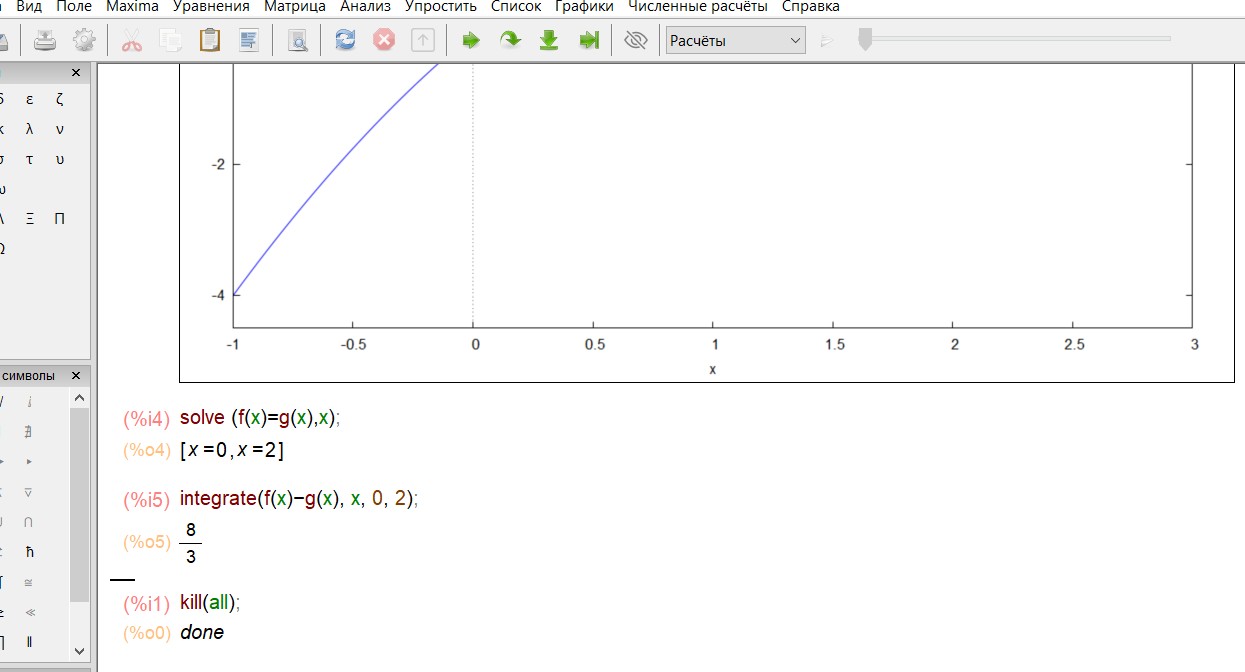
Пример 3.
Вычислить площадь фигуры, ограниченной следующими линиями
y 4 , y = 0, ???? = 4, ???? = 0, ???? = 4.
x
Зададим функции
y 4 , y = 0, ???? = 4,
x
Вертикальные прямые ???? = 4 ???? = 0 в Maxima можно построить только, представив их уравнения в параметрическом виде:
x 4
y t
и x 0 .
y t
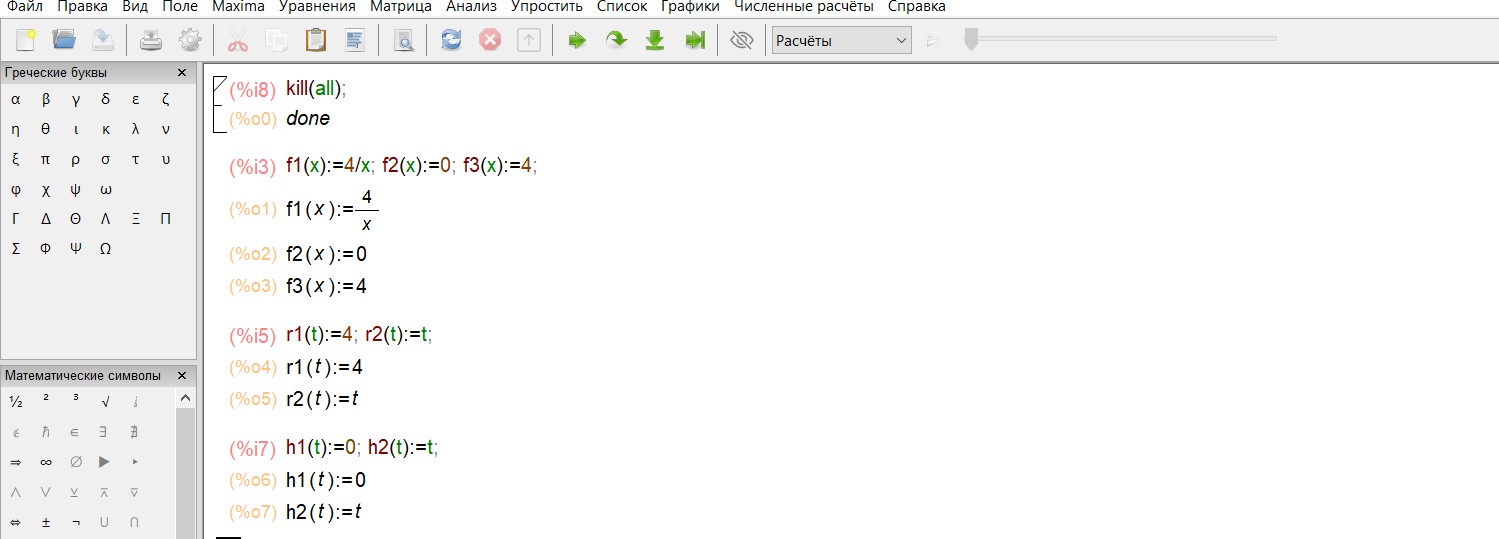
Теперь построим графики всех этих функций:
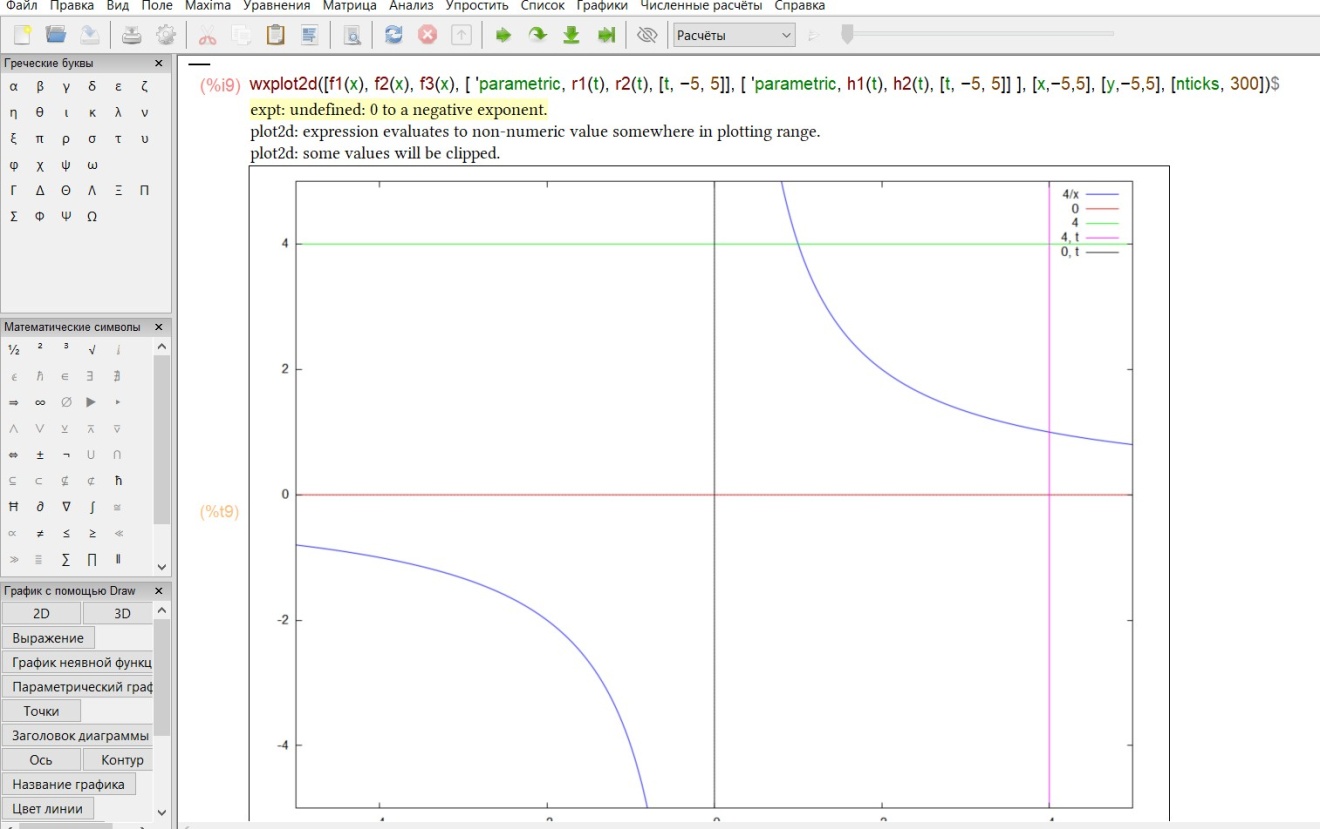
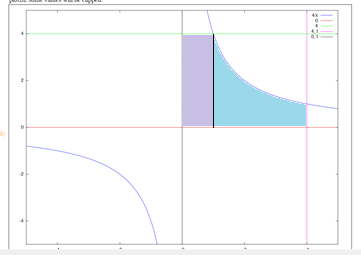 Чтобы вычислитьплощадь интересующей нас фигуры, необходимо поделить область на две части: от прямой х=1.
Чтобы вычислитьплощадь интересующей нас фигуры, необходимо поделить область на две части: от прямой х=1.Первая фигура является прямоугольником, ее площадь равна S1 4 1 4 . Площадь второй фигуры вычисляем с помощью определенного интеграла:

Площадь искомой фигуры равна
4 4 ln 4 .



 ЗАДАНИЕ 1(Вариант 8)
ЗАДАНИЕ 1(Вариант 8)
 Задача 1. Вычислить площадь фигуры, ограниченной графиками функций (аналитически и с помощью программы wxMaxima). Выполнить построение.
Задача 1. Вычислить площадь фигуры, ограниченной графиками функций (аналитически и с помощью программы wxMaxima). Выполнить построение.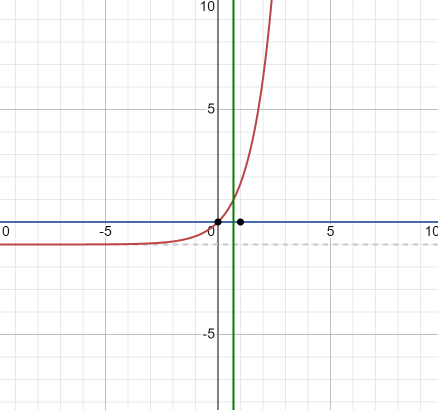
Аналитически решим задачу следующим образом. Найдем точки пересечения графиков функций y=e^x-1 и y=0:
e^x - 1 = 0
e^x = 1
x = ln(1)
x = 0
Точка пересечения графика функции y=e^x-1 и оси OX: (0,0)
Точка пересечения вертикальной линии x=ln2 и оси OX: (ln2,0)
Таким образом, фигура ограничена графиками функций y=e^x-1, y=0 и вертикальной линией x=ln2. Для нахождения площади фигуры нужно вычислить интеграл от e^x-1 до 0 по переменной x в пределах от 0 до ln2:
S = ∫[0,ln2] [e^x-1]dx
S = [e^x - x] [0,ln2]
S = e^ln2 - ln2 - (e^0 - 0)
S = 2 - ln2
Ответ: площадь фигуры, ограниченной графиками функций
y=e^x-1,
y=0,
x=ln2 равна 2 - ln2.
Теперь выполним построение этой фигуры в программе wxMaxima. Для начала определим функции:
f(x) := exp(x)-1;
g(x) := 0;
Затем построим графики этих функций и вертикальной линии x=ln2:
draw2d(
terminal = 'svg,
xrange=[-1,2],
yrange=[-1,3],
color=red,
key=false,
title="График функции y=e^x-1",
xlabel="x",
ylabel="y",
f(x),
g(x),
vertical_line(ln(2))
);
Результатом будет изображение графика функции y=e^x-1, оси координат, горизонтальной линии y=0 и вертикальной линии x=ln2. Площадь фигуры можно найти с помощью интегрирования или подсчета площади методом трапеций.
| 1 | y x 23 , y 4x 8. | 2 | y x 9 x2 , y 0, 0 x 3. |
| 3 | y 4 x2 , y x2 2x. | 4 | y sin xcos2 x, y 0, 0 x 2. |
| 5 | y 4 x2 , y 0, x 0, x 1. | 6 | y x2 4 x2 , y 0, 0 x 2. |
| 7 | y cos xsin2 x, y 0, 0 x 2. | 8 | y ex1, y 0, x ln 2. |
| 9 | y 1 , y 0, x1 ln x x 1, x e3 . | 10 | y arccos x, y 0, x 0. |
| 11 | y x12 , y2 x1. | 12 | y 2x x2 3, y x2 4x 3. |
| 13 | y x 36 x2 , y 0, 0 x 6. | 14 | x arccos y, x 0, y 0. |
| 15 | y arctg x, y 0, x 3. | 16 | y x2 8 x2 , y 0, 0 x 2 2 . |
| 17 | x ey1, x 0, y ln 2. | 18 | y x 4 x2 , y 0, 0 x 2. |
| 19 | y x , y 0, 1 x x 1. | 20 | y 1 , y 0, 1 cos x x 2, x 2. |