Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 142
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Вычислить несобственный интеграл приближенно.
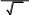Задача 3.Проверить результат вычислений с помощью встроенных функций программы wxMaxima.
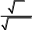
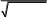
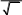
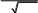
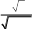
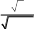
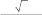
Используем замену переменной: x = t / (1 - t), dx = dt / (1 - t)^2
Тогда границы интегрирования изменятся на [0, 1].
Подставляем новую переменную в функцию f(x):
f(t) = e^(-t^2 / (1 - t)^2) / (1 - t)^2
Применяем метод трапеций:
I = h * (f(a)/2 + Σ(f(xi)) + f(b)/2)
где h = (b - a) / n, xi = a + i * h, i = 1, 2, ..., n-1.
Выбираем количество интервалов n таким образом, чтобы оценка погрешности была меньше заданной точности:
E <= 0.001, где E - оценка погрешности.
Используем встроенную функцию trapz программы wxMaxima для проверки результата.
ex2 dx
0
Задача 1. Подберем число A так, чтобы интеграл
числить приближенно с точностью до 0.0001.
ex2 dx
0
можно было вы-
Из неравенства Тогда
x2 2Ax A2 (x A)2 0
следует
x2 2Ax A2 .
2 Ax
2 A2
ex2 dx
e2 Ax A2 dx eA2 e2 Axdx eA2 e
eA2 e e.
A A A
e32
2A A
2A 2A
Легко проверить, что
0.00005 .
2 3 2
Очевидно, что достаточно взять
A 3.
3
ex2 dx ex2 dx ex2 dx.
0 0 3
Задача 2. Теперь вычислим с помощью метода трапеций (или другого выше
3
рассмотренного) определенный интеграл e x2 dx. Верхний предел оценен
0
выше.
Результат вычисления: 0.8861936233658585. Отрезок интегрирования был разбит на 3 части.
3
Задача 3. Вычислим интеграл e x2 dx
0
с помощью встроенной функции
romberg.
Оценим остаток несобственного интеграла ex2 dx
3
с помощью встроенного
пакета quadpack.
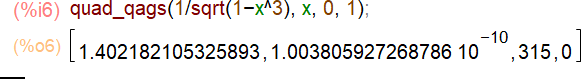
Как мы видим, результат 1.957719323677975*10^-5, что меньше 0.00005.
0.5
dx
0
Задача 1. Найдем такое положительное число , чтобы интеграл
0.5 dx
был вычислен с точностью до .
0
Точкой бесконечного разрыва подынтегральной функции является
концевая точка
x 0. Найдем искомое значение , для которого выполняет-
ся неравенство (4.2) для левого конца:
f xdx
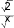0
.
2
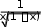Так как
при
x0;0.5, то
dx
2 dx
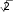2
2 .
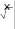
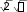0
Задача 3.Проверить результат вычислений с помощью встроенных функций программы wxMaxima.| 1 | 2 x 2 xdx 0 | 21 | 2 x 3 3 dx 0 8 x |
| 2 | arctgx x(2 x) dx 1 | 22 | arctgx 5 dx 1 x |
| 3 | 1 x3 3 3 x dx 0 | 23 | 3 2x1 4 x 2 dx 2 |
| 4 | dx e3 xx3 1 | 24 | dx x(1 x3) 1 |
| 5 | 1 3 x2 1 xdx 0 | 25 | 3 x 3 xdx 1 |
| 6 | arctgx 3 dx 1 1 x | 26 | arctgx x2 (1 x) dx 1 |
| 7 | 2 x2 x1 dx 1 | 27 | 0 x2 1 1 xdx 1 |
| 8 | dx 5 1 x x1 | 28 | dx exx x 1 |
| 9 | 0 4 x x2 5 2 dx 1 x | 29 | 1 1 x 3 dx 0 1 x |
| 10 | arctgx 3 2 dx 1 x x | 30 | arctgx x3 xdx 1 |
| 11 | 1 x2 2 3 x 1 dx 1 | 31 | 2 4 x3 4 x2 1 dx 1 |
| 12 | x2 x4 2 x3 dx 1 | 32 | dx 5 10 1 x x x 1 |
| 13 | 2 3 x2 4 2 xdx 1 | 33 | 0 dx 2 1 3 x(2 x) |
| 14 | arctgx x(1 x2 ) dx 1 | 34 | dx e2 xx2 1 |
| 15 | 2 x 2 4 3 dx 0 x | 35 | 1.5 dx 3 1 x1 |
| 16 | dx e4 xx4 1 | 36 | dx x2 x 1 1 |
| 17 | 1 2 x 4 dx 0 1 x | 37 | 2 x 2 dx 1 4 x |
| 18 | arctg2x 4 dx 1 4 x | 38 | xarctgx 2 x3 dx 1 |
| 19 | 1,5 dx 3 x(2 x) 0 | 39 | 0.5 dx 4 x(2 x) 0 |
| 20 | dx 3 2 1 x x 2 | 40 | x x 2 x3 dx 1 |
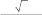
Используем замену переменной: x = t / (1 - t), dx = dt / (1 - t)^2
Тогда границы интегрирования изменятся на [0, 1].
Подставляем новую переменную в функцию f(x):
f(t) = e^(-t^2 / (1 - t)^2) / (1 - t)^2
Применяем метод трапеций:
I = h * (f(a)/2 + Σ(f(xi)) + f(b)/2)
где h = (b - a) / n, xi = a + i * h, i = 1, 2, ..., n-1.
Выбираем количество интервалов n таким образом, чтобы оценка погрешности была меньше заданной точности:
E <= 0.001, где E - оценка погрешности.
Используем встроенную функцию trapz программы wxMaxima для проверки результата.
Примеры выполнения задания.
Пример 1.
ex2 dx
0
Задача 1. Подберем число A так, чтобы интеграл
числить приближенно с точностью до 0.0001.
ex2 dx
0
можно было вы-
Из неравенства Тогда
x2 2Ax A2 (x A)2 0
следует
x2 2Ax A2 .
2 Ax2 A2
-
A2
ex2 dx
e2 Ax A2 dx eA2 e2 Axdx eA2 e
eA2 e e.
A A A
e32
2A A
2A 2A
Легко проверить, что
0.00005 .
2 3 2Очевидно, что достаточно взять
A 3.
3
ex2 dx ex2 dx ex2 dx.
0 0 3
Задача 2. Теперь вычислим с помощью метода трапеций (или другого выше
3
рассмотренного) определенный интеграл e x2 dx. Верхний предел оценен
0
выше.
Результат вычисления: 0.8861936233658585. Отрезок интегрирования был разбит на 3 части.
3
Задача 3. Вычислим интеграл e x2 dx
0
с помощью встроенной функции
romberg.
Оценим остаток несобственного интеграла ex2 dx
3
с помощью встроенного
пакета quadpack.
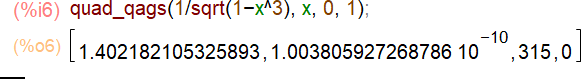
Как мы видим, результат 1.957719323677975*10^-5, что меньше 0.00005.
Пример 2.
0.5
dx
0
Задача 1. Найдем такое положительное число , чтобы интеграл
0.5 dx
был вычислен с точностью до .0
Точкой бесконечного разрыва подынтегральной функции является
концевая точка
x 0. Найдем искомое значение , для которого выполняет-
ся неравенство (4.2) для левого конца:
f xdx
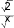0 .
2 Так как при
x0;0.5, то
dx
2 dx
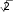2 2 .
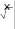
0