Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 149
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
print("Значение интеграла:", result)
Значение интеграла: 0.15076181319431824
b
Задача 9. Вычислить интеграл f(x)dxметодом трапеций.
а
import numpy as np
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
a = 0.4 # нижний предел интегрирования
b = 1.2 # верхний предел интегрирования
n = 100 # количество разбиений
dx = (b - a) / n # шаг сетки
result = 0 # инициализациярезультата
for i in range(n):
x1 = a + i*dx
x2 = a + (i+1)*dx
result += (integrand(x1) + integrand(x2)) * dx / 2
print("Значение интеграла:", result)
Значение интеграла: 0.14887375069617526b
Задача 10. Вычислить интеграл f(x)dxметодом Симпсона.
a
import numpy as np
def integrand(x):
return np.exp(2*x)*np.sin(3*x)
a = 0.4 # нижний предел интегрирования
b = 1.2 # верхний предел интегрирования
n = 100 # количество разбиений (должно быть четным)
if n%2 != 0:
n += 1 # увеличиваем n, чтобы было четным
dx = (b - a) / n # шаг сетки
result = 0 # инициализация результата
for i in range(int(n/2)):
x1 = a + 2*i*dx
x2 = x1 + dx
x3 = x2 + dx
result += (integrand(x1) + 4*integrand(x2) + integrand(x3)) * dx / 3
print("Значение интеграла:", result)
Значение интеграла: 0.14717267733238303
В задачах 7-10 обеспечить точность вычислений
0.001.
Пример выполнения задания.
0
Зададим интеграл (x2 2x1) sin(3x)dx.
1
Задача 1. Вычислим непосредственно с помощью формулы Ньютона-
Лейбница определенный интеграл
x2 2x 1sin 3xdx
1
Для вычисления интеграла применим метод интегрирования по частям:
0 u x2 2x 1 du (2x 2)dx
x2 2x 1sin 3xdx
1
dv sin 3xdx v
1
cos3x
3
 1 0
1 0 1 0
1 2 0
x2 2x 1 cos3x

2x 2cos3xdx


x 1cos3xdx

3
u x 1
1
du dx
3 1
1 2 1
3 3 1
 0 1 0
0 1 0 1

(x 1) sin 3x
-
sin 3xdx
dv cos3xdx v sin 3x
 3
3 3 3 3
1 3 1
1 2 0 1 1 cos3x




0 1 1 1 cos3 7 2 cos3 -0.18592648




3 3 3 3
1 3 9 27 27
Задача 2. Найдем неопределенный интеграл с помощью программы wxMaxima.
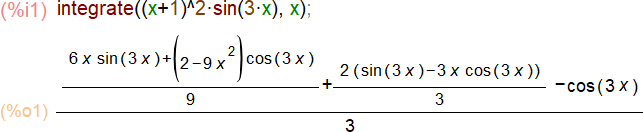
Задача 3. Вычислим определённый интеграл.
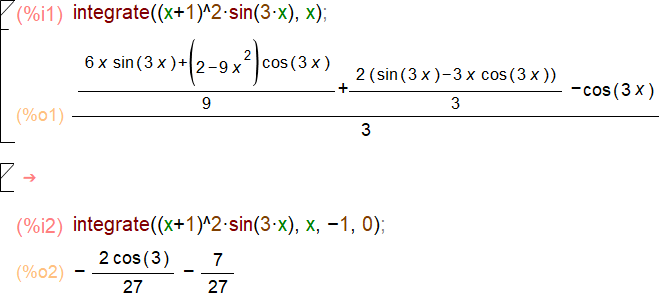
Задача 4. Вычислим определённый интеграл посредством встроенной функ- ции приближенного вычисления quadpack.

В ячейке вывода массив результата вычисления содержит:
-0.1859264817333003– приближённое значение интеграла; 2.064198609078587*10^-15 – относительная погрешность вычислений; 21 – число интервалов разбиения;
0 – признак корректности вычислений (0 – без проблем).
Задача 5. Вычислим определённый интеграл посредством встроенной функ- ции приближенного вычисления romberg(f(x), x, a, b);

Задача 6. Применим метод левых прямоугольников.

Задана точность вычислений
0 . 0 0. Для определения количества
отрезков разбиения, обеспечивающих заданную точность, был организован
цикл. Получили 0.185607624168928.
n14 , а результат вычисления интеграла: -
Задача 7. Применим метод средних прямоугольников.

Точность 7.652390164653022*10^-5, результат вычисления: - 0.1859519914907337.
Для обеспечения заданной точности интервал был разделен на 35 отрезков. Для определения числа отрезков
, соответствующих точности 0.001, необхо- димо создать цикл.
Результат вычисления: -0.1859519914907337. Точность 7.652390164653022*10^-5.
Задача 8. Применим метод правых прямоугольников.

Для обеспечения заданной точности интервал был разделен на 70 отрезков. Для определения числа отрезков необходимо создать цикл.
Результат вычисления: -0.1859137266631504. Точность 3.8264827583262*10^-5.
Задача 9. Применим метод трапеции.

Для обеспечения заданной точности интервал был разделен на 10 отрезков. Для определения числа отрезков необходимо создать цикл.
Результат вычисления: -0.1853015587248992. Точность 6.246081200169395*10^-4.
Задача 10. Применим метод Симпсона.

Для обеспечения заданной точности интервал был разделен на 2 отрезка. Для определения числа отрезков необходимо создать цикл.
Результат вычисления: -0.1859123439526545. Точность 2.219513808524957*10^-5.
3. Приближенное вычисление несобственных интегралов
К несобственным интегралам относятся интегралы, которые имеют хотя бы один бесконечный предел интегрирования или подынтегральную функцию, имеющую разрыв второго рода – обращающуюся в бесконечность хотя бы в одной точке отрезка интегрирования.
-
Интегралы от разрывных функций
-
Если подынтегральная функция в некоторых внутренних точках ci
-
i 1, 2,.. отрезка интегрирования a,b имеет разрыв первого рода
(скачок), то интеграл следует вычислять для каждого участка непрерывности отдельно, а результаты складывать. Например, в случае одной точки разрыва
первого рода типа скачка (рис. 6)
x c
( a c b) имеем
b c b
f xdx f xdx f xdx.
a a c
 y
yx
0 a c b
Рис. 6. Пример функции, имеющей разрыв первого рода в точке
x c.
Для вычисления каждого из интегралов в правой части полученного равенства можно использовать любой из рассмотренных в данной главе методов.
-
Если подынтегральная функция имеет разрыв второго рода
(бесконечный) в некоторой внутренней точке cотрезка интегрирования
a,b, тогда по определению полагают
b c1 b
f xdx lim f xdx f xdx
(4.1)
10
2
a 0
a c2
На отрезках a,c 1
и c 2 ,b
подынтегральная функция не имеет
особенностей (рис. 6) и соответствующие интегралы