Файл: Министерство транспорта российской федерации федеральное государственное образовательное учреждение высшего профессионального образования.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 158

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯМОСКОВСКИЙ ГОСУДАРСТВЕННЫЙТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИКафедра аэродинамики, конструкции и прочностилетательных аппаратовЕфимов В.В. ОСНОВЫ АВИАЦИИЧасть I ОСНОВЫ АЭРОДИНАМИКИ И ДИНАМИКИПОЛЕТА ЛЕТАТЕЛЬНЫХ АППАРАТОВдля студентов 1 курса специальности 061100всех форм обученияМосква - 2003Рецензенты: д.т.н., проф. Ципенко В.Г., д.т.н., проф. Калугин В.Т.Ефимов В.В.Основы авиации. Часть I. Основы аэродинамики и динамики полета летательных аппаратов: Учебное пособие. - М.: МГТУ ГА, 2003. - 64 с.Данное пособие издается в соответствии с учебным планом для студентов 1- го курса специальности 061100 всех форм обучения.Рассмотрено и одобрено на заседаниях кафедры 08.04.03 и методического совета 29.04.03. Содержание ВведениеУчебное пособие «Основы аэродинамики и динамики полета летательных аппаратов» посвящено одному из разделов дисциплины «Основы авиации», предусмотренной учебным планом подготовки студентов 1-го курса специальности 061100.В настоящем учебном пособии основные сведения из аэродинамики и динамики полета излагаются в максимально упрощенной форме. Это связано с тем, что студенты 1-го семестра 1-го курса не знакомы с математическим аппаратом, необходимым для фундаментального изучения этих наук. Однако для того, чтобы грамотно решать задачи повышения экономической эффективности летательных аппаратов (ЛА), которые будут стоять в будущем перед выпускниками данной специальности, достаточно владеть материалом в том объеме, который предлагается ниже.Пособие состоит из двух частей. В первой части излагаются основы аэродинамики: дается представление о строении земной атмосферы и свойствах воздуха, вводится понятие стандартной атмосферы, рассмотрены свойства воздуха и основные законы аэродинамики, физика взаимодействия воздуха с обтекаемыми телами.Вторая часть пособия посвящена динамике полета. В ней рассматривается движение центра масс ЛА, а также движение ЛА вокруг его центра масс, т.е. вопросы устойчивости и управляемости.В конце пособия дан список литературы, которая при желании или необходимости может быть использована для более глубокого изучения материала. 1. Основы аэродинамики летательных аппаратовАэродинамика - это наука об общих законах движения газа (преимущественно воздуха), а также о взаимодействии газа с движущимися в нем телами. Это взаимодействие может быть механическим и тепловым, в результате чего на ЛА в процессе его полета в атмосфере действуют аэродинамические силы, происходит нагрев его поверхности. Именно благодаря аэродинамическим силам возможен полет самолета или вертолета, т.е. аппаратов тяжелее воздуха. Однако аэродинамические силы не только поднимают ЛА в воздух, но и создают вредное сопротивление его движению, а нагрев поверхности ЛА приводит к изменению прочностных характеристик его конструкции. Величины аэродинамических и тепловых нагрузок зависят от формы ЛА и режимов его полета (скорости, высоты). В связи с этим основной задачей аэродинамики является выбор рациональной внешней формы ЛА с целью получения заданных летно-технических характеристик (ЛТХ), а также определение аэродинамических нагрузок и тепловых потоков, действующих на поверхность ЛА, для прочностных расчетов. Строение атмосферы Полеты ЛА гражданской авиации происходят в атмосфере Земли, поэтому при создании и эксплуатации ЛА необходимо учитывать строение и параметры атмосферы (давление, плотность, температуру).Рассмотрим строение атмосферы. Атмосферой называют газовую оболочку, которая благодаря воздействию гравитационного поля Земли удерживается ею и вращается вместе с планетой как единое целое. Плотность воздуха и атмосферное давление максимальны у поверхности Земли, а с подъемом на высоту постепенно уменьшаются. Воздух, составляющий атмосферу, представляет собой механическую смесь газов. В нижних слоях атмосферы содержание газов в объемных долях следующее: азот (N2) 78 %, кислород (О2) 21 %, аргон (Аг) 0,93 %, другие газы (в том числе СО2 - углекислый газ)

Тс = 288,15 К; рс = 101300 Па; рс = 1,225 кг/м3; ас = 340,29 м/с; vc = 1,46 • 1(Г5 м2/с.Изменение параметров стандартной атмосферы по высоте представляют, как правило, в табличной форме. Однако для тропосферы (до высоты 11 км) основные параметры стандартной атмосферы приближенно можно рассчитать по следующим формулам: (9a) Тн= ТС- 0,0065Н; / х-,5,256 Ph = Pc 1- <44300 )_, TT \-15,256 (96) = pc 1- <44300 )_ (9b) Основы кинематики и динамики воздуха В аэродинамике при изучении движения воздуха иногда удобнее использовать не модель сплошной среды, а модель, рассматривающую среду как совокупность множества частиц. В этой модели движение частиц представляют в виде траекторий и линий тока. Траекторией движения частицы называется геометрическое место точек, в которых частица находилась в процессе своего движения. При этом вектор скорости частицы в всех точках траектории направлен по касательной к ней (см. рис. 4). Линия тока - это линия, составленная из точек, в которых движущиеся частицы находятся в фиксированный момент времени, причем векторы скоростей частиц направлены по касательной к этой линии так же, как и в случае с траекторией. Траектория и линия тока различаются тем, что траектория описывает движение одной частицы в разные моменты времени, а линия тока - движение совокупности частиц в каждый фиксированный момент времени. При определенном условии траектория и линия тока совпадают. Это происходит в том случае, если в каждой фиксированной точке линии тока вектор скорости не изменяется с течением времени по величине и направлению. Такое течение называется установившимся . При неустановившемся течении вектор скорости со временем изменяется, что приводит к изменению формы линии тока, и она уже не совпадает с траекторией движения отдельной частицы. Рис. 4. Траектория частицыПредставим себе замкнутую линию и через точки этой линии проведем линии тока. В результате получим замкнутую поверхность, образованную линиями тока. Такая поверхность называется трубкой тока. Поскольку, как следует из определения линии тока, векторы скорости движения частиц направлены по касательной к поверхности трубки тока, то эта поверхность является непроницаемой для частиц воздуха. Воздух, движущийся внутри трубки тока, называется струйкой. Струйка называется элементарной, если ее поперечное сечение достаточно мало и можно считать, что в каждый фиксированный момент времени скорости частиц воздуха в этом сечении равны. Рассмотрим такую струйку (см. рис. 5). Рис. 5. Элементарная струйкаПоскольку поверхность трубки тока непроницаема для частиц воздуха, то при установившемся течении через каждое поперечное сечение элементарной струйки в единицу времени будет протекать одна и та же масса воздуха. Это вытекает из закона сохранения массы, если принять, что трубка тока не имеет разрывов, через которые может поступать или уходить воздух.Поэтому формула, описывающая это явление, называется уравнением неразрывности и имеет вид:т = р 17*’ = const, (10)где т - масса воздуха, протекающего через поперечное сечение струйки в единицу времени;р - плотность воздуха в данном сечении струйки;V- скорость воздуха в данном сечении струйки;F- площадь поперечного сечения струйки.Для малых скоростей течения (при М < 0,3) можно принять, что воздух несжимаем, т.е. плотность воздуха не меняется от сечения к сечению (р = const). Тогда ее можно исключить из уравнения (10) и, возвращаясь к рис. 5, записать:KiFi = V2F2. (11)Из этого уравнения можно сделать важный вывод: при уменьшении площади поперечного сечения струйки скорость течения воздуха в ней возрастает, а при увеличении - падает. Но это справедливо только для дозвуковых течений (М < 1). При сверхзвуке (Л7 > 1) картина меняется с точностью до наоборот. Здесь уже важную роль играет сжимаемость. Например, при уменьшении площади поперечного сечения плотность воздуха увеличивается настолько, что в целом произведение Fp возрастает, а это приводит к уменьшению скорости потока V (см. формулу (10)). Поэтому при сверхзвуковом потоке для того, чтобы увеличить скорость, необходимо также увеличивать площадь поперечного сечения струйки.Важное место в аэродинамике отводится также закону сохранения энергии, который используется для получения взаимосвязи давления и скорости воздуха в струе. На рис. 6 показана струйка при виде сбоку. Рассмотрим относительно некоторого уровня баланс энергии масс воздуха, проходящих через сечения 1 и 2 за одинаковый промежуток времени АЛ Движение воздуха в струйке будем считать установившимся, а сжимаемость и трение учитывать не будем. Выделим для рассмотрения некоторую массу воздуха т, проходящую через сечение 1 со скоростью V\ за время Л/. Эта масса обладает т К2 кинетической энергией, равной —и имеет потенциальную энергию, равную работе силы тяжести mgh\. Кроме этого, на рассматриваемую массу воздействует сила давления воздуха p\F\, лежащего выше сечения 1, поэтому необходимо также учесть работу, совершаемую этой силой. Работа, как известно, равна произведению силы на перемещение, которое в данном случае можно вычислить, умножив скорость V\ на промежуток времени Л?, в тече-ние которого рассматриваемая масса воздуха проходит через сечение 1. Согласно закону сохранения суммарная энергия рассматриваемой массы воздуха при прохождении ею сечения 2 не изменится, поэтому можно записать: P\F\V\t±t + + mgh i= P2F2V2^t + + mghi • (12)1 Рис. 6. Движение воздуха в струйкеВ соответствии с уравнением (11) объем воздуха, проходящий через сечение 1 должен быть равен объему воздуха, проходящего через сечение 2: F\V\/St — F2V2At -Поделим уравнение (12) на уравнение (13) и получим:PK12 Z PVl /Pi +—^ + Pghi= Р2 +—^ + pgh2. (14)(13) Или: (15)pF2 р + + pgn = const. (16)Мы получили уравнение Бернулли для газа без учета сжимаемости. Если пренебречь действием силы тяжести или предположить, что движение воздуха происходит в горизонтальной плоскости, то потенциальная энергия рассматриваемой массы воздуха не изменится, и из выражения (15) произведение pgh можно исключить: рЕ2 р + = const. 2Слагаемоер называется статическим давлением, а слагаемое Рг2 - динамическим давлением (или скоростным нано-ром). Сумма же статического и динамического давлений называется полным давлением и обозначается р$.pV2Pq = р+ = const.При внимательном рассмотрении уравнения Бернулли можно заметить, что при увеличении скорости потока динамическое давление будет расти, а статическое соответственно - падать, т.к. их сумма изменяться не должна. Так, при обтекании тела набегающим потоком воздуха (см. рис. 7) на его носке существует точка А (критическая точка), в которой скорость потока из- за полного торможения равна 0. В этой точке динамическая составляющая равна нулю, а статическое давление максимально и равно полному давлению. В любой другой точке поверхности тела скорость потока будет больше 0, а это значит, что статическое давление будем меньше, чем в критической точке. Рис. 7. Обтекание тела набегающим потокомВзаимосвязь статического и динамического давлений хорошо иллюстрируется на примере функционирования прибора, который носит название трубка Пито - Прандтля, или в технике - приемник воздушного давления (ПВД). Этот прибор широко используется в авиации для определения скорости полета. Схематично трубка Пито - Прандтля изображена на рис. 8. Прибор имеет две полости, соединенных с манометром. Когда трубка выставлена вдоль вектора скорости набегающего потока, то в полости 1 давление воздуха будет равно полному давлению, т.к. это критическая точка и поток в ней полностью тормозится. Полость 2 сообщается с потоком через боковое отверстие в трубке, при этом линии тока проходят мимо этого отверстия, не искажаясь. За счет этого в полости 2 действует только статическое давление, а влияние динамического давления исключено. Разность давлений в полостях 1 и 2, измеряемая с помощью манометра, будет равна скоростному напору:рИ2^ = Рор. (18)Отсюда, зная плотность воздуха, легко определить скорость набегающего потока (или скорость полета). Основы аэродинамики самолета До сих пор мы рассматривали взаимодействие набегающего потока с неким абстрактным телом. Однако в авиации эксплуатируются вполне конкретные летательные аппараты: самолеты, вертолеты, планеры, аэростаты, дирижабли и др. Все они, так или иначе, взаимодействуют с окружающим воздухом в процессе своего полета. Среди всего многообразия видов летательных аппаратов, созданных человеком, наибольшее распространение получил самолет. Самолет - это летательный аппарат тяжелее воздуха, который имеет крыло для создания подъемной силы и силовую установку для создания тяги. Геометрические характеристики основных частей самолета Основными частями самолета являются: крыло, фюзеляж, оперение, шасси, силовая установка, бортовое оборудование (см. рис. 9). В данном разделе нас интересуют, прежде всего, те части самолета, которые непосредственно взаимодействуют с набегающим потоком воздуха и создают основную долю аэродинамических сил, т.е. крыло, фюзеляж и оперение. Шасси и силовая установка, как правило, тоже обтекаются потоком воздуха, но в данном курсе мы не будем заострять на этом внимание. Рис. 9. Общий вид самолетаКрыло предназначено для создания подъемной силы, которая уравновешивает силу тяжести, действующую на самолет, а также обеспечивает изменение траектории полета. Подъемная сила на крыле появляется во время движения самолета относительно окружающего воздуха. Этот эффект создается благодаря тому, что крыло имеет определенную форму, которая характеризуется в свою очередь формой профиля, формой крыла при виде сверху (формой крыла в плане) и при виде спереди.Профиль крыла - это сечение крыла плоскостью, параллельной плоскости симметрии самолета. Это плоскость, относительно которой большинство элементов самолета располагаются симметрично слева и справа, ее иногда называют базовой плоскостью самолета.Формы профилей разнообразны, они выбираются, прежде всего, исходя из соображений обеспечения требуемых летно-технических характеристик самолета. На рис. 10 приведены наиболее распространенные формы профилей. Геометрические характеристики профиля показаны на рис. 11. Для описания формы профиля используют такие геометрические характеристики, как хорда, относительная толщина, относительная вогнутость и др. Хордой профиля называется отрезок прямой, соединяющий две наиболее удаленные точки профиля. Хорда обозначается, как правило, буквой Ь. Формы верхнего и нижнего контуров профиля задаются с помощью таблиц с координатами точек или в виде аналитических зависимостей: ув =/(х) и уи = f (х). При этом начало системы координат располагают в передней точке хорды, а саму хорду - на оси Ох. - двояковыпуклый симметричный двояковыпуклый несимметричный выпукло-вогнутый Рис. 10. Формы профилей - суперкритический Рис. 11. Геометрические характеристики профиляОтносительная толщина профиля равна отношению максимальной толщины профиля к его хорде, выраженному в процентах:— _ Опах . 1 оо % , (19)44300>44300>1   2   3   4   5   6

ьгде с111ах - наибольшее расстояние между точками профиля, лежащими на прямой, перпендикулярной хорде: с111ах = (ук -ун)тах.В зависимости от типа самолета величина относительной толщины профиля колеблется в пределах от 2 до 20 %. Сверхзвуковые самолеты имеют крылья с тонкими профилями (до 5 %), у дозвуковых - профили крыльев толще (как правило, свыше 10 %).Положение максимальной толщины профиля по длине хорды определяется относительной координатой:хс= — -100%, (20)bгде - абсцисса максимальной толщины профиля. Величина для дозвуковых самолетов колеблется в пределах 25 4- 30 %, для сверхзвуковых - 40 -ь 50 %.Средняя линия профиля - это геометрическое место точек, соответствующих серединам отрезков, соединяющих точки профиля, лежащие на прямой, перпендикулярной хорде, т.е. это координаты середин толщин профиля: уср(х) = 0,5[ув(х) + дУ*)].Относительная вогнутость профиля - это отношение максимальной вогнутости профиля к его хорде, выраженное в процентах:/ = ^-400%, (21)ьгде /пах - максимальная по абсолютной величине ордината средней линии профиля, т.е. максимальное отклонение средней линии профиля от хорды, ее еще называют стрелой прогиба: = 0,5(ув +^н)тах-Относительная вогнутость профилей современных самолетов находится в пределах 0 -ь 4 %.Вогнутость профиля иногда называют кривизной профиля. Положение максимальной вогнутости по длине хорды определяется относительной координатой:Xf=^

Рис. 21. Траекторная система координатУглом пути называется угол между проекцией вектора Ик на горизонтальную плоскость XgQZg и осью 0Xg. Угол наклона траектории 0 - это угол между вектором земной скорости VK и местной горизонтальной плоскостью XgQZg. Аэродинамические силы и моменты, действующие на самолет Механическое воздействие набегающего потока на самолет сводится к нагрузкам, непрерывно распределенным по его поверхности. Для удобства изучения эти распределенные нагрузки приводят к результирующей силе, приложенной в центре масс самолета, которая называется аэродинамической силой и обозначается (см. рис. 22), а также моменту вокруг центра масс, который называется аэродинамическим моментом и обозначается М. Рис. 22. Аэродинамическая сила и аэродинамический момент, действующие на самолет при его обтекании набегающим потокомТеоретические и экспериментальные исследования показали, что величина аэродинамической силы прямопропорциональна скоростному напору рК2 набегающего потока и характерной площади обтекаемого тела S'.pV2Ra=Cr^-S, (32)где Cr - коэффициент пропорциональности, который носит название коэффициента аэродинамической силы.Аэродинамический момент также прямопропорционален скоростному рИ2напору , характерной площади S и характерному линейному размеру обтекаемого тела Г.рИ2М = I, (33)где m - коэффициент пропорциональности, который называется коэффициентом аэродинамического момента.За характерную площадь и характерный размер берутся соответственно площади и размеры тех частей самолета, которые вносят основную долю в создание рассчитываемой силы или момента.Разложим аэродинамическую силу Ra на составляющие по осям связанной и скоростной систем координат. В связанной системе координат эти проекции обозначаются и называются следующим образом:X - аэродинамическая продольная сила;Y - аэродинамическая нормальная сила;Z - аэродинамическая поперечная сила.В скоростной системе координат:Ха - сила лобового сопротивления;Ya - аэродинамическая подъемная сила;Za - аэродинамическая боковая сила.На рис. 23 показаны проекции аэродинамической силы Ra на оси связанной и скоростной систем координат при отсутствии скольжения. Рис. 23. Разложение аэродинамической силы по осям связанной и скоростной систем координат при Р = ОВ дальнейшем мы будем иметь дело в основном с проекциями аэродинамической силы на оси скоростной системы координат. Воспользовавшись формулой (32), запишем выражения для этих проекций. При этом в качестве характерной будем брать характерную площадь того элемента, который играет основную роль в создании данной силы.Так, сила лобового сопротивления самолета складывается из сил лобового сопротивления фюзеляжа, крыла, оперения и других частей самолета. За характерную площадь можно принять площадь миделевого сечения фюзеля- жа ^м.ф- (34)pV2у —Г нq а ^ха °м.ф ->где Сха - коэффициент лобового сопротивления.В создании подъемной силы самолета основную роль играет крыло, поэтому в качестве характерной берется площадь крыла S^: (35)pV2у — С нQ 1 а уа °кр 5где Суа - коэффициент подъемной силы.Аэродинамическая боковая сила в основном определяется вертикальным оперением и фюзеляжем, значительно меньший вклад в создание этой силы вносят крыло, горизонтальное оперение и другие части самолета. Поскольку вертикальное оперение является основным элементом при создании боковой силы (оно для этого предназначено), то его площадь SB 0 и принимают за характерную: (36), рУ2 <,za ^в.о? где Cza - коэффициент боковой силы.Так как аэродинамические моменты, действующие на самолет, рассчитываются в основном относительно связанных осей координат, найдем проекции момента М на оси связанной системы координат (см. рис. 24). Аэродинамический момент относительно оси ОХ называется моментом крена. Он определяется в основном силами, действующими на крыло самолета и в меньшей степени - на вертикальное и горизонтальное оперения:рИ2(37) где тх - коэффициент момента крена.Аэродинамический момент относительно оси ОУ называется моментом рыскания. Он создается силами, действующими в основном на вертикальное оперение и фюзеляж. Этот момент вычисляется по следующей формуле:рИ2M* = myX^-S в.о£в.о, (38)где mv - коэффициент момента рыскания;£в.о - плечо вертикального оперения (расстояние от точки приложения аэродинамической силы, возникающей на вертикальном оперении, до центра масс самолета).Аэродинамический момент относительно оси 0 Z называется моментом тангажа. Он создается силами, действующими на крыло, горизонтальное оперение и фюзеляж. Вертикальное оперение практически не участвует в создании момента тангажа. Момент тангажа вычисляют по формуле:рИ2Mz = mz —, (39)где mz - коэффициент момента тангажа. Подъемная сила Рассмотрим обтекание двояковыпуклого симметричного профиля идеальным газом (см. рис. 25). Профиль считается симметричным, если он симметричен относительно хорды. Пусть он сначала установлен под углом атаки ос = 0. В данном случае угол атаки равен углу между вектором скорости набегающего потока V и хордой профиля. Рис. 25. Обтекание симметричного профиля при ос = О (без образования подъемной силы)У носка профиля в передней критической точке А происходит полное торможение потока, статическое давление в этой точке максимально и равно полному давлению. Далее поток разделяется на два: один обтекает верхнюю поверхность профиля, другой - нижнюю. У задней кромки профиля потоки опять сливаются в задней критической точке В. В точке В также как и в точке А скорость потока равна 0, потому что здесь сходятся линии тока, идущие по верхней и нижней поверхностям профиля, а частица газа не может одновременно двигаться по двум направлениям. Следовательно, в точке В статическое давление также как и в точке А максимально и равно полному давлению. Но между точками А и В статическое давление отличается от полного давления. Это является следствием того, что в процессе движения от точки А к точке В площади поперечных сечений струек сначала уменьшаются, а потом растут. При этом в соответствии с уравнением неразрывности (10) скорость в струйках будет соответственно сначала расти, а затем падать. Из закона сохранения энергии в аэродинамике (см. уравнение Бернулли (16)) следует, что при увеличении скорости статическое давление уменьшается. Значит, от точки А до точки В на верхней и нижней поверхностях профиля будут располагаться зоны относительного разрежения. Поскольку мы рассматриваем симметричный профиль, то величины падения статического давления в этих зонах будут одинаковыми. Это значит, что в направлении, перпендикулярном вектору скорости набегающего потока, на профиль не будет воздействовать составляющая аэродинамической силы, названная выше подъемной.Очевидно, что для того, чтобы получить подъемную силу нужно сделать профиль несимметричным или установить симметричный профиль под некоторым углом атаки ос ф 0 (см. рис. 26).Рассмотрим обтекание профиля потоком под углом атаки ос > 0. В этом случае струйка, обтекающая профиль сверху будет иметь большее сужение,чем струйка, обтекающая профиль снизу, а значит скорость в верхней струйке будет больше, чем в нижней (VB > VH). Это приведет к тому, что на верхней поверхности профиля статическое давление будет меньше, чем на нижней (ръ < /?„). Из-за этой разности образуется аэродинамическая подъемная сила, направленная вверх. а) обтекание несимметричного профиля при ос = О б) обтекание симметричного профиля при ос > ОРис. 26. Обтекание профилей с образованием подъемной силыЕстественно предположить, что чем больше угол атаки или вогнутость профиля, тем больше будет и подъемная сила. Рассмотрим вначале влияние угла атаки на подъемную силу симметричного профиля. В формуле подъемной силы (35) имеется коэффициент, который зависит от угла атаки - это коэффициент подъемной силы Cva. График зависимости Cva от ос для симметричного и несимметричного профилей представлен на рис. 27, из которого видно, что при малых углах атаки коэффициент подъемной силы зависит от ос линейно. Рис. 27. Зависимость коэффициента подъемной силы от угла атакиЕсли профиль имеет положительную относительную вогнутость, то кривая Cva = /(ос) смещается плоскопараллельно вверх. Угол атаки, при котором Суа = О обозначается ОСО, в данном случае осо< 0. Легко видеть, что при одном и том же угле атаки профиль, имеющий большую относительную вогнутость, будет иметь больший коэффициент подъемной силы.На больших углах атаки нарушается плавное обтекание профиля. Это происходит из-за влияния вязкости на движение частиц в пограничном слое. В процессе движения вдоль верхней поверхности профиля частицы воздуха будут терять скорость. На каком-то этапе им не хватит кинетической энергии, чтобы двигаться дальше вдоль поверхности. В итоге на некотором участке верхней поверхности профиля произойдет отрыв пограничного слоя. Это явление приводит к нарушению линейности зависимости Cva = /(ос). При увеличении угла атаки зона отрыва также будет увеличиваться, но коэффициент подъемной силы Суа при этом продолжает расти и достигает своего максимального значения С/тах. Угол атаки, который соответствует Суатах, называется критическим углом атаки оскр (см. рис. 28). Величина критического угла атаки, как правило, не превышает 20°. При дальнейшем увеличении угла атаки отрыв потока достигнет интенсивности, при которой коэффициент подъемной силы будет резко падать. Рис. 28. Соответствие максимального значения коэффициента подъемной силы критическому углу атаки Сила лобового сопротивления Выше мы отметили, что сила лобового сопротивления складывается из сил, действующих на все части самолета, обтекаемые потоком. Но для упрощения и сокращения объема излагаемого материала рассмотрим только силу лобового сопротивления, возникающую на крыле самолета. Соответственно в качестве характерной площади будем использовать площадь крыла.Сила лобового сопротивления крыла складывается из сил различной природы. В общем случае силу лобового сопротивления можно представить в виде следующей суммы:Ха= X а тр + X а д + X а j + X а вл (40)где Хатр - сила сопротивления трения;Хал - сила сопротивления давления;Xai - сила индуктивного сопротивления;1   2   3   4   5   6

Рис. 38. Влияние механизации крыла на вид зависимости Cva = f (ос)Кроме использования описанной выше механизации крыла для улучшения взлетно-посадочных характеристик самолета используются различные энергетические методы. Они основаны на использовании энергииосновных или вспомогательных силовых установок. Здесь может использоваться сжатый воздух, отбираемый от компрессора, струя воздуха, выдуваемая из сопла реактивного двигателя, а также воздух, отбрасываемый воздушным винтом. Эти мероприятия позволяют привнести дополнительную энергию в поток, что затягивает отрыв пограничного слоя на больших углах атаки. При этом также растет скорость потока, обдувающего крыло, что непосредственно увеличивает подъемную силу. 2. Основы динамики полета летательных аппаратовДинамика полета - это наука о движении ЛА. Различают движение центра масс ЛА (траекторное движение) и движение ЛА вокруг его центра масс. К первому виду движения относятся горизонтальный полет ЛА, набор высоты, снижение, взлет, посадка, вираж и др. В процессе же движения вокруг центра масс ЛА может накреняться набок, задирать или опускать нос, поворачиваться влево или вправо, иными словами, ЛА может вращаться вокруг центра масс. При этом ЛА должен сохранять устойчивость своего положения в пространстве и обладать управляемостью.Рассмотрим сначала траекторное движение, а затем перейдем к устойчивости и управляемости. Траекторное движение самолета Уравнения движения центра масс самолета Самолет движется в воздухе под действием аэродинамической силы Ra , силы тяги двигателей Р и силы тяжести G. С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор Р обычно располагается в базовой плоскости самолета и образует некоторый угол с осью ОХ связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор Р приложен в центре масс.Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.Установившийся горизонтальный полет - это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39).Уравнения движения центра масс самолета запишутся в этом случае следующим образом:Pcos а = Ха-,Ya + Psin a = G.Поскольку угол атаки ос мал (при этом cos ос ® 1, a sin ос ® 0), то можно записать: Рис. 39. Схема сил, действующих на самолет в установившемся горизонтальном полете(49) Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета Егп.Учитывая, что G = mg (где т - масса самолета, a g - ускорение свободного падения), можно записать:Cye^S^mg, (50)откуда:к (51)Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха р (которая зависит от высоты полета),площади крыла Л'кр и коэффициента подъемной силы Cva. Поскольку Cva напрямую зависит от угла атаки ос, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.Установившийся набор высоты - прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории 0, показана на рис. 40. Рис. 40. Схема сил, действующих на самолет при установившемся наборе высоты (угол атаки принят малым и не показан)В этом случае уравнения движения примут вид:'Р = Ха + G sin 0;Ya =G cos 0.Необходимо отметить, что при наборе высоты тяга двигателей Р уравновешивает не только силу лобового сопротивления Ха, как в горизонтальном полете, но и составляющую силы тяжести GsinO. Подъемная сила Ya при этом требуется меньшая, поскольку GcosO < G.Важной характеристикой самолета является его скороподъемность - вертикальная скорость набора высоты Vv. Из рис. 40 видно, что:Vy=VHadSinO. (53)Установившееся снижение - прямолинейное движение самолета вниз с постоянной скоростью. На рис. 41 показана схема сил, действующих на самолет при снижении. Местная горизонтальная плоскость Рис. 41. Схема сил, действующих на самолет при установившемся снижении (угол атаки принят малым и не показан) Уравнения движения для установившегося снижения имеют вид:\Р = Ха -Gsin9;\ (54)Ya =G cos 9.Если мы поделим первое уравнение системы (54) на второе, то получим:tSd-^уУ (55)Из уравнения (55) видно, что установившееся снижение возможно только, если тяга меньше лобового сопротивления (Р<Ха). Обычно снижение происходит при малых значениях тяги (при тяге малого газа), поэтому можно принять, что Р



Характерной точкой, представляющей особый интерес, является т о ч - к а «3», которая является точкой касания прямой, проведенной из начала координат к кривой потребных тяг Рп = f (И). Очевидно, что в данной точке от-

Рц

ношение -р- будет минимальным. При выполнении этого условия, как это станет ясно в дальнейшем, обеспечивается максимальная дальность полета.

В точке «4» потребная тяга Рп минимальна. Перепишем формулу (47) для условий установившегося горизонтального полета:

(64)

Если Рп - минимальна, то аэродинамическое качество К будет максимальным. В разделе, посвященном аэродинамическому качеству (см. и. 1.6.6), мы отметили, что коэффициент подъемной силы и угол атаки, соответствующие максимальному значению качества называются наивыгоднейшими. Отсюда и скорость, соответствующая минимальному значению потребной тяги также называется наивыгоднейшей и может быть вычислена по формуле:

и. = J 2mg„ ■ (65)

У ^JY/НвР^Кр

При дальнейшем уменьшении скорости для обеспечения установившегося горизонтального полета наряду с увеличением угла атаки необходимо увеличивать тягу двигателей, т.к. здесь начинает быстро расти индуктивное сопротивление, что приводит к общему увеличению потребной тяги.

Точка «6» соответствует минимальному значению скорости установившегося горизонтального полета При этом значении скорости необходимо, чтобы самолет летел с максимальным значением коэффициента подъемной силы Cva max, т.е. на критическом угле атаки оскр. По соображениям безопасности полет на критическом угле атаки считается недопустимым, т.к. любая ошибка в пилотировании или вертикальный порыв ветра, приводящие к дальнейшему увеличению угла атаки, вызовут резкое уменьшение Cva из-за отрыва потока на крыле, что приведет к сваливанию самолета. Поэтому на практике за минимально допустимую скорость полета принимают ско

рость, несколько большую, чем Kmjn (см. точку «5»). Коэффициент подъемной силы при этом берут несколько меньшим: Суа
доп * 0,8...0,85С1йтах. Минимально допустимая скорость полетавычисляется по формуле:

К ДОП = (66)

min л кгл о V 7

У ^^ддопР^кр

С помощью диаграммы потребных и располагаемых тяг можно легко определить максимальную скороподъемность J^max на данной высоте и соответствующую ей скорость набора высоты VHa6.

Из уравнений движения при наборе высоты (52) вытекает, что:


mg

Из формулы (69) видно, что скороподъемность зависит от избытка тяги (Рр-Рп)« Очевидно, что максимальная скороподъемность будет при максимальном избытке тяги, т.е. когда разность (Рр - Рп) максимальна. Найти эту максимальную разность и соответствующую ей скорость набора высоты Инаб можно графически (см. рис. 42), а затем по формуле (69) рассчитать максимальную скороподъемность Vy max на данной высоте.

С увеличением высоты полета располагаемая тяга падает, а минимальные значения потребной тяги не изменяются (см. рис. 43).



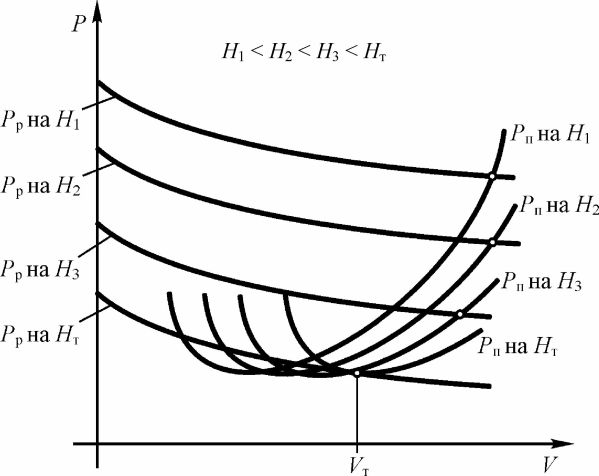
Рис. 43. Изменение потребной и располагаемой тяг в зависимости от

высоты полета

Наступает такой момент, когда кривые потребных и располагаемых тяг имеют только одну точку пересечения (при этом Vv тах= 0). На этой высоте установившийся набор высоты невозможен, а установившийся горизонтальный полет возможен только на скорости VT. Такая высота называется теоретическим потолком самолета. Однако достичь теоретического потолка самолет в установившемся наборе высоты практически не может, т.к. время набора высоты при этих условиях стремится к бесконечности. Поэтому вводится понятие практического потолка - высоты полета, при которой максимальная скороподъемность не меньше заданной. Для дозвуковых самолетов Vvmax > 3...5 м/с.

  1. Дальность и продолжительность полета

Дальность и продолжительность полета - одни из важнейших летнотехнических характеристик самолета. Дальность полета Д - это максимальное расстояние, которое может преодолеть самолет, израсходовав определенный запас топлива. Продолжительность полета Д - промежуток времени, затрачиваемый на достижение дальности полета.


Различают техническую и практическую дальность полета.

Технической дальностью называют максимальную дальность полета самолета в стандартных атмосферных условиях, без ветра при полной заправке самолета топливом и полной его выработке, за исключением невырабатываемого остатка. Наличие невырабатываемого остатка связано с тем, что не все заправленное в баки самолета топливо может быть выработано, что связано с конструктивными особенностями топливной системы. Обычно невырабатываемый остаток топлива составляет 1,5 % от массы заправляемого запаса топлива.

Техническая дальность является важным показателем предельных возможностей самолета. Однако завершение реального полета с пустыми баками является недопустимым по соображениям безопасности, т.к. любое непредвиденное отклонение от маршрута, наличие встречного ветра и т.п. могут привести к тому, что самолет не достигнет аэродрома назначения. Поэтому более реальным показателем является практическая дальность полета.

Практическая дальность - это максимальная дальность полета самолета в стандартных атмосферных условиях, без ветра при полной заправке самолета топливом и полной его выработке, за исключением невырабатываемого остатка, а также заданного заранее аэронавигационного запаса топлива.

Аэронавигационный запас топлива предназначен для компенсации возможных отклонений условий полета от расчетных, а также для ожидания в воздухе в районе аэродрома назначения или достижения запасного аэродрома в случае возникновения особых обстоятельств. Аэронавигационный запас топлива составляет, как правило, 10... 15 % от массы заправляемого топлива.

Дальность полета £п складывается из следующих участков (см. рис. 44):

£наб - дальность набора высоты;

Дфейс - дальность крейсерского полета;

£сн - дальность снижения.


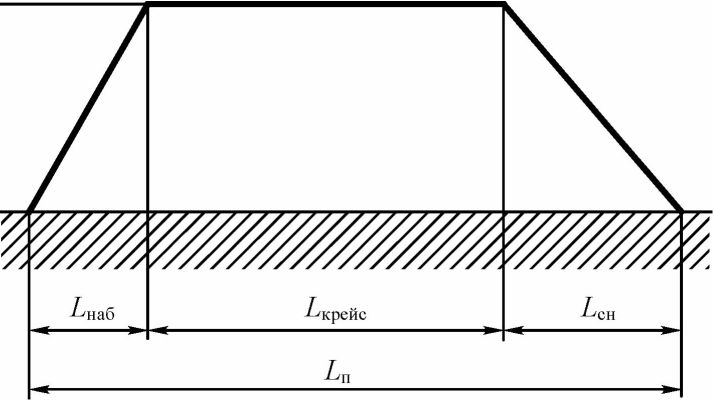
Рис. 44. Профиль полета самолета




Крейсерский полет - это основной этап полета, на котором преодолевается большая часть расстояния (до 95 %) между аэродромами вылета и назначения. Крейсерский полет проходит, как правило, с постоянной скоростью на постоянной высоте (или в заданном диапазоне высот - эшелоне). В первом приближении его можно считать установившимся горизонтальным полетом.

При выборе высоты и скорости крейсерского полета стремятся к тому, чтобы минимизировать расход топлива. Различают часовой и километровый расходы топлива. Дальность полета £Крейс вычисляют, используя километровый расход топлива, а продолжительность /крейС - используя часовой расход топлива:


(70)

(71)
т

-^крейс — э Q км

где тт - расходуемая масса топлива [кг];

(/км - километровый расход топлива [кг/км].

т т
tкрейс = s

(/ч

где (/ч - часовой расход топлива [кг/ч].

Часовой расход топлива q4- расход массы топлива за один час пути. Часовой расход топлива рассчитывается по формуле:

дч = сУдРп, (72)

где сУд - удельный часовой расход топлива (расход массы топлива за один




час пути на единицу тяги
кг

Н-ч




Из формулы (72) видно, что наименьшим часовой расход (/4min будет при минимальной потребной тяге Рп min (точка «4» на диаграмме потребных и располагаемых тяг (см. рис. 42)), т.е. на наивыгоднейшей скорости Полет при этом согласно формуле (71) будет иметь максимальную продолжитель-

ность. Из формулы (64) вытекает, что Pnmin = , поэтому :

-^Мпах



(73)
cyRmg

Ц ч min —

шах

Часовой расход топлива стремятся минимизировать, если основная задача полета связана не с транспортной операцией, а, например, с патрулированием, когда важна именно продолжительность полета. Если же выполняется перевозка грузов, то при этом важно обеспечить заданную дальность полета. Для этого стараются минимизировать километровый расход.

Километровый расход топлива дкм - расход массы топлива на один километр пути. Километровый расход топлива равен:

94 СУД^П

9км — — , ' /ЧД

где V- скорость полета, которая имеет размерность [км/ч].

Из формулы (74) видно, что километровый расход топлива будет ми- нимальным, когда минимально отношение —. Ранее при рассмотрении диаграммы потребных и располагаемых тяг (см. рис. 42) мы отметили характерную точку «3», в которой как раз выполняется это условие. Соответствующая этой точке скорость будет скоростью крейсерского полета ЕКрейс, обеспечивающего максимальную дальность на данной высоте полета при заданном запасе топлива.

Как километровый, так и часовой расходы топлива уменьшаются с увеличением высоты полета. Поэтому в качестве крейсерской высоты полета рекомендуется выбирать высоту практического потолка, если нет других ограничений (например, отсутствие герметичной кабины на самолете). Необходимо отметить, что в процессе полета по мере расходования топлива масса самолета уменьшается, в результате чего постепенно возрастает высота практического потолка. Если самолет будет постоянно лететь на высоте практического потолка, т.е. с небольшим набором высоты, то в этом случае дальность его полета будет больше, чем при горизонтальном полете. Такой способ выполнения крейсерского полета получил название полета по потолкам .

  1. Движение самолета вокруг центра масс

Чтобы заставить самолет двигаться по заданной траектории летчик должен иметь возможность управлять величиной и направлением сил, действующих на самолет. На современных транспортных самолетах летчик может, выбирая режим работы двигателей, управлять величиной тяги, а также, используя рули, изменять ориентацию самолета относительно набегающего потока воздуха и поверхности Земли с целью обеспечения необходимой величины и направления аэродинамической силы, при этом он может использовать также механизацию крыла. Если в процессе полета обеспечивается требуемое значение сил и моментов, действующих на самолет, то такое движение самолета называется опорным. Установившимся опорным движением будет такое движение, при котором суммы сил и моментов, действующих на самолет равны нулю, т.е. самолет находится в состоянии равновесия.

Однако реальное движение самолета отличается от опорного. На самолет в полете случайным образом воздействуют порывы ветра, пульсации тяги двигателей, неточные действия летчика и др. Чтобы упростить управление самолетом необходимо обеспечить парирование случайных возмущений и возвращение самолета к опорному движению без участия летчика.

Если задача организации опорного движения связана с управляемостью самолета, то задача парирования возмущающих воздействий связана с его устойчивостью.

Устойчивость и управляемость самолета являются его важными свойствами, определяющими возможность и безопасность полета, требуемые усилия летчика при управлении самолетом, уровень комфорта экипажа и пассажиров в полете. Требования к характеристикам устойчивости и управляемости являются обязательными и нормируются для самолетов различных классов.

2.2.1. Управляемость самолета

Управляемостью самолета называется его способность изменять параметры опорного движения в ответ на целенаправленные действия летчика или автоматических устройств.

Самолет может поворачиваться вокруг любой из осей связанной системы координат, поэтому управляемость разделяют на:

продольную (по тангажу) - вокруг оси О Z;

путевую (по рысканию) - вокруг оси ОУ;

поперечную (по крену) - вокруг оси ОХ.

Как отмечалось выше (см. и. 1.6.8) для управления самолетом по тангажу, рысканию и крену используются аэродинамические рули (руль высоты, руль направления и элероны соответственно). Для обеспечения заданного опорного режима полета углы отклонения этих рулей, подбираются таким образом, чтобы выполнялось следующее условие:

< My = 0- (75)

Mz = 0.

Отклонения рулей, обеспечивающие выполнение условия (75), называются балансировочными, т.е. обеспечивающими баланс моментов.

На современных самолетах пост управления самолетом организован таким образом, что для управления рулем высоты и элеронами используется ручка управления (или штурвал). А для управления рулем направления - педали. Для управления рулем высоты летчик отклоняет ручку управления самолетом (или штурвальную колонку) от себя или на себя, а для управления элеронами - влево или вправо (при использовании штурвального управления летчик поворачивает штурвал подобно рулевому колесу автомобиля).

В качестве примера рассмотрим продольную управляемость самолетом. На рис. 45 показана схема сил, действующих на самолет нормальной аэродинамической схемы. Из рисунка видно, что момент, возникающий от действия подъемной силы крыла Ya кр, уравновешивается моментом от подъемной силой горизонтального оперения YaT0 (для простоты примем, что силы лобового сопротивления Ха и тяги двигателей Р приложены в центре масс самолета и моментов не создают):

^акр-^кр — YamLY0, (76)

где £кр и £го - расстояния от центра масс самолета до точек приложения подъемной силы крыла и горизонтального оперения соответственно.



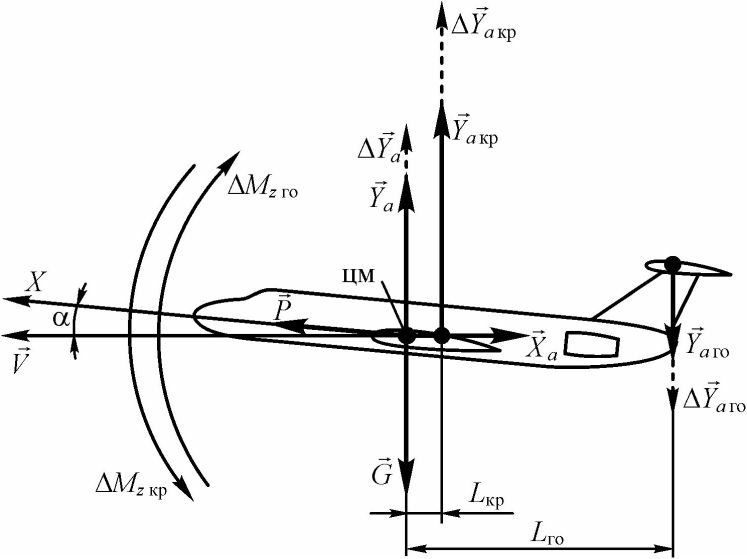
Рис. 45. Схема сил и моментов, действующих на самолет при обеспечении продольной управляемости

Кроме этого, равнодействующая подъемных сил крыла и горизонтального оперения Ya = Ya кр - Ya го уравновешивается силой тяжести самолета G:

Ya =G. (77)

Для того, чтобы самолет поднял нос вверх и увеличил угол атаки, летчик отклоняет ручку управления (или штурвальную колонку) на себя. Система управления передает это движение на руль высоты, и он в результате отклоняется вверх, изменяя вогнутость профиля и создавая на горизонтальном оперении приращение подъемной силы ДУаГ0, направленное вниз (см. рис. 45). Это приращение силы, в свою очередь, создает приращение момента тангажа AA/zro = ДУаГ0£Г0, заставляющего выйти самолет из состояния равновесия и начать вращение вокруг оси ОZ. После достижения самолетом некоторого угла атаки произойдет увеличение подъемной силы крыла на величину ЛУдкр- Это вызовет приращение момента тангажа АЛ/гкр = Л А,крЛкр, уравновешивающее AA/zro, т.е. AA/ZKp = AA/zro. Таким образом, моменты относительно оси ОZ вновь будут сбалансированы, но уже на новом угле атаки.

Если перед началом маневра опорное движение самолета было установившимся, т.е. не только сумма моментов, но и сумма сил была равна нулю, то теперь из-за разницы плеч (£кр < £го) приращение подъемной силы крыла будет больше приращения подъемной силы горизонтального оперения: ДУакр > ЛЕаГо, т.е. равнодействующая подъемных сил крыла и горизонтального оперения получит приращение ДУа. Это значит, что суммарная подъемная сила самолета не будет уравновешена силой тяжести (Ya + ДУа > G), и самолет будет осуществлять ускоренное движение вверх с перегрузкой nv > 1 по криволинейной траектории.

Таким образом, имеется четкая взаимосвязь между перемещением ручки управления самолетом хв и возникающей перегрузкой nv. Эта взаимосвязь

(Их в характеризуется производной ——, которая является одним из основных dnv

показателей управляемости самолета.

Для отклонения ручки управления самолетом летчику необходимо приложить усилие Ръ. Оно будет тем больше, чем больше отклонение хв. Это связано с тем, что с увеличением отклонения руля высоты 8В возрастает шарнирный момент. Аэродинамическим шарнирным моментом Мш называется момент аэродинамической силы, действующей на руль, относительно оси вращения руля. Шарнирный момент, действующий на руль высоты, будет равен (см. рис. 46):

МШ=УВ/Ш, (78)

где Ув - аэродинамическая сила, действующая на руль высоты;

1Ш - расстояние от оси вращения руля до точки приложения силы Yn.

При отклонении руля шарнирный момент возрастает за счет увеличения аэродинамической силы, действующей на него.



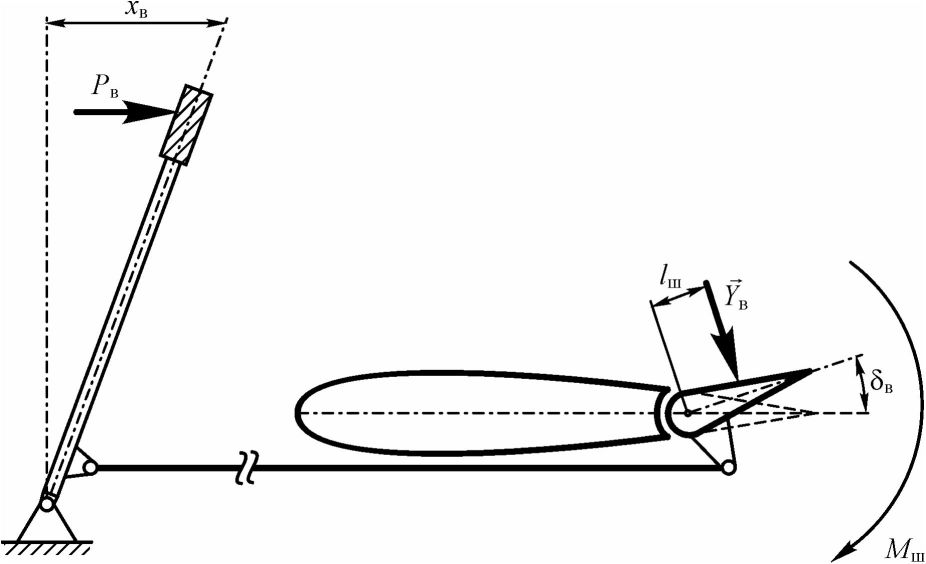
Рис. 46. Кинематическая схема продольного управления самолетом

Из представленной на рис. 46 упрощенной кинематической схемы продольного управления самолетом видно, что при отклонении ручки управления самолетом на величину хв руль высоты отклонится на угол 8в. Летчик при этом должен приложить усилие Рв, чтобы скомпенсировать шарнирный момент Мт. Таким образом, можно записать следующее равенство:

PBdxB=Мшй6в. (79)

Откуда:

РВ=^МШ=КШМШ, (80)

ах в

где Кш = - передаточный коэффициент в системе продольного

dx в

управления самолетом.

Поскольку усилие на ручке управления Рв однозначно связано с ее перемещением хв, а как мы отмечали выше, перемещение хв связано с перегрузкой nv, то и усилие Рв будет связано с перегрузкой nv. Поэтому еще одним по- dPB

казателем управляемости самолета является производная , характери-

dnv

зующая скорость нарастания усилия на ручке управления для создания требуемой перегрузки.

Аналогичным образом строятся показатели путевой и поперечной управляемости самолета.

  1. Устойчивость самолета

Устойчивостью самолета называется его способность без участия летчика сохранять заданный опорный режим полета, возвращаясь к нему после отклонения, вызванного воздействием внешних возмущений, после того, как это воздействие прекратится.

Различают статическую и динамическую устойчивость.

Статически устойчивым самолетом называют самолет, у которого отклонение какого-либо параметра движения приводит к появлению силовых факторов, стремящихся уменьшить это отклонение. Если возникающие силовые факторы приводят к увеличению первоначальных отклонений, то самолет считается статически неустойчивым. Пилотировать такой самолет крайне трудно, т.к. летчик вынужден постоянно вмешиваться в управление, чтобы парировать случайно возникающие отклонения параметров движения от опорных значений.

Процесс восстановления опорного режима полета носит, как правило, колебательный характер. Продолжительность этого процесса характеризует динамическую устойчивость самолета. К другим характеристикам динамической устойчивости относятся также: амплитуда движений, период колебаний и др. Ниже мы будем рассматривать только статическую устойчивость.

Статическая устойчивость, как и управляемость, делится на продольную, путевую и поперечную, при этом путевая и поперечная устойчивости объединены в боковую устойчивость.

2.2.2.1. Продольная статическая устойчивость самолета

Продольная статическая устойчивость самолета - это его способность без участия летчика противодействовать изменению угла атаки.

Рассмотрим продольную статическую устойчивость самолета при воздействии на него восходящего порыва ветра. Восходящий порыв ветра увеличивает угол атаки самолета на величину Дос (см. рис. 47). Приращение угла атаки Дос вызовет в свою очередь приращения подъемных сил крыла ДУ),кр и горизонтального оперения ДУа го, направленные вверх. Суммарное приращение подъемной силы самолета ДУа = ДУ),кр + ДУа го будет приложено в точке, называемой фокусом самолета по углу атаки. Если фокус рас

положен позади центра масс самолета (как на рассматриваемом рисунке), то возникнет момент ЛЛ/г, опускающий нос самолета, т.е. возвращающий самолет на прежний угол атаки.




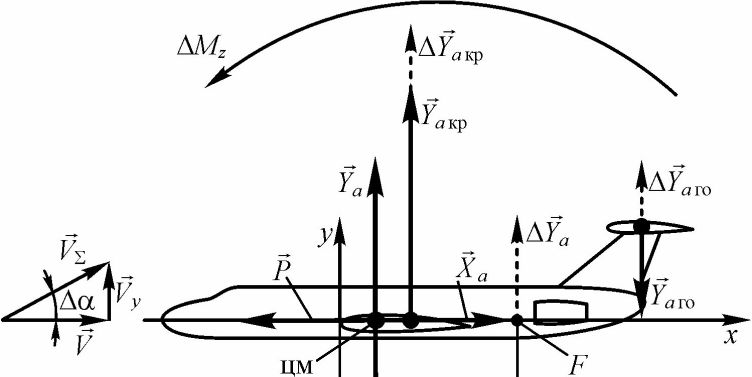
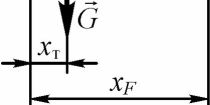
Рис. 47. Возникновение силовых факторов, обеспечивающих продольную
статическую устойчивость

Количественно продольная статическая устойчивость самолета оценивается степенью продольной статической устойчивости суг, которая в первом приближении может быть вычислена по формуле:

су z =xT-xF, (81)

_ хт

где хт = относительная координата цента масс самолета;

ЬА

xF = —— - относительная координата фокуса самолета по углу атаки. ЬА

Координаты хт и Хр отсчитываются от носка САХ.

Легко видеть, что если суг < 0, то самолет статически устойчив, если суг > 0, то самолет статически неустойчив, если же суг = 0, то самолет является статически нейтральным.

  1. Путевая статическая устойчивость самолета

Путевая статическая устойчивость самолета - это его способность без участия летчика противодействовать изменению угла скольжения.

Если в опорном движении скольжение отсутствовало и появилось (ДР), например, в результате горизонтального порыва ветра (см. рис. 48), то возникнет приращение боковой силы AZa, которое складывается из приращения боковой силы вертикального оперения AZaB0 и приращения боковой силы фюзеляжа AZa ф:

Д2д = AZaB0 +А2дф. (82)

Статически устойчивый в путевом отношении самолет под действием приращения момента AA/V начнет вращение вокруг оси ОУ, пытаясь устранить возникшее скольжение Ар. Но это произойдет только в том случае, если фокус самолета по углу скольжения, где будет приложено приращение боковой силы AZa, расположен позади центра масс. Необходимо отметить, что приращения боковой силы фюзеляжа AZa ф носит, как правило, дестабилизирующий характер, т.е. создает момент, пытающийся развернуть самолет на еще больший угол скольжения.


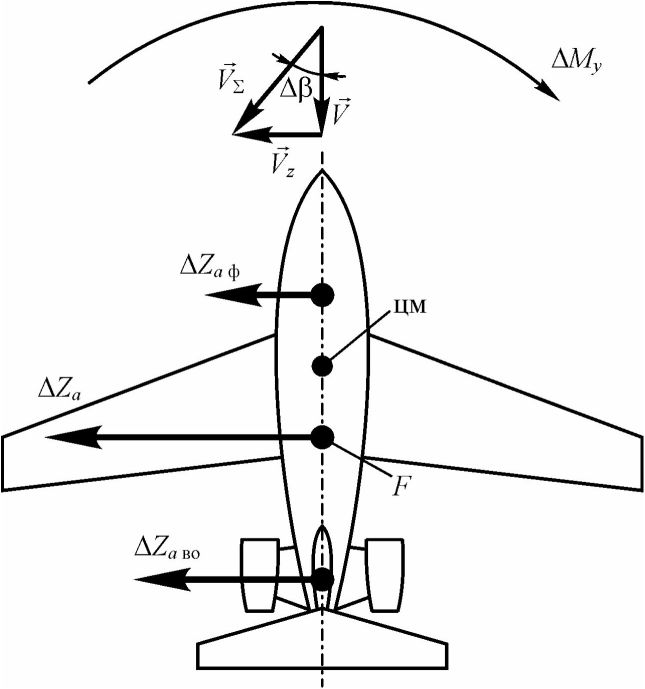
Рис. 48. Возникновение силовых факторов, обеспечивающих путевую статическую устойчивость





(83)
Для количественной оценки путевой статической устойчивости используется показатель, называемый степенью путевой статической устойчивости:

-у JC jz 2

где хт = относительная координата цента масс самолета;

^кр

- Хр 1

xF = относительная координата фокуса самолета по углу сколь-

^кр

жения.

Следует помнить, что чаще всего фокус по углу атаки не совпадает с фокусом по углу скольжения.

  1. Поперечная статическая устойчивость самолета

Поперечная статическая устойчивость самолета - это его способность без участия летчика противодействовать изменению угла крена.

Если по той или иной причине самолет накренился, например, на левое полукрыло на некоторый угол Ду (см. рис. 49), то возникшая проекция силы тяжести на поперечную ось ОZ, равная GsinAy, приведет к появлению скольжения на это полукрыло. Статически устойчивый самолет по определению должен устранить появившийся крен. Рассмотрим, при каких условиях это возможно.



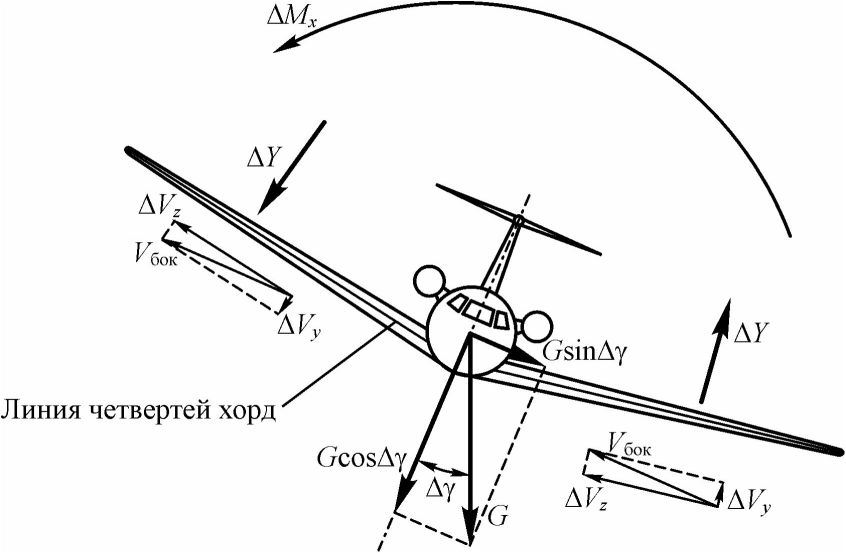
Рис. 49. Возникновение силовых факторов, обеспечивающих поперечную статическую устойчивость

В результате скольжения на левое полукрыло появляется поток воздуха, обдувающий самолет сбоку с некоторой скоростью Еб0К- Если самолет имеет положительное поперечное V крыла как на рис. 49, то эта скорость будет раскладываться на две составляющие: параллельную линии четвертей хорд полукрыла ДЕг и перпендикулярную ей Л Vv. Приращение скорости Л Vz никак не влияет на подъемную силу, а приращение AEV вызывает увеличение угла атаки на левом полукрыле и его уменьшение на правом. Это значит, что подъемная сила на левом полукрыле станет больше, чем на правом. В результате возникнет момент ЛАД, стремящийся повернуть самолет вокруг оси ОХ на устранение крена. Таким образом, положительное поперечное V крыла создает стабилизирующий момент, а отрицательное - дестабилизирующий.

Смотрите также файлы