Файл: Министерство транспорта российской федерации федеральное государственное образовательное учреждение высшего профессионального образования.docx

Увеличение подъемной силы крыла при использовании механизации происходит в основном за счет увеличения коэффициента подъемной силы Суа, а также за счет некоторого увеличения площади крыла Л'_кр.

Выше было показано, что чем больше вогнутость профиля, тем больше будет и коэффициент подъемной силы C_va при том же угле атаки. Чтобы увеличить вогнутость профиля применяется механизация задней кромки крыла (см. рис. 36).


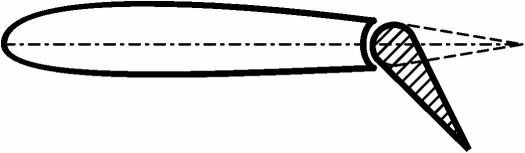
- щиток

- простой закрылок
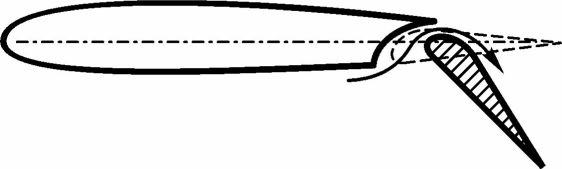
- выдвижной однощелевой закрылок


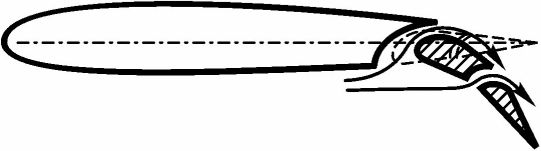
Рис. 36. Средства механизации задней кромки крыла
- выдвижной многощелевой закрылок

Простейшей механизацией задней кромки крыла является отклоняемый вниз щиток. Выдвижной щиток позволяет не только увеличить вогнутость профиля в выпущенном положении, но и увеличить площадь крыла. Простой закрылок также лишь увеличивает вогнутость профиля, а выдвижной, кроме того, позволяет увеличить площадь крыла. Чаще всего выдвижной закрылок делается щелевым. Щель создается для того, чтобы воздух с нижней поверхности крыла мог перетекать на верхнюю поверхность и ускорять поток, обдувающий закрылок сверху. Это делается для того, чтобы при больших углах отклонения закрылка не происходило отрыва пограничного слоя с его поверхности.

Механизация передней кромки (см. рис. 37) слабо влияет на вогнутость профиля, по крайней мере, этим влиянием можно пренебречь. Ее роль заключается в том, чтобы затянуть начало отрыва пограничного слоя на большие углы атаки. Это позволяет повысить максимальное значение C_va за счет увеличения критического угла атаки. Щитки Крюгера и отклоняемые носки в выпущенном положении уменьшают пик разрежения в районе носовой части профиля, предотвращая тем самым отрыв потока в этом месте. Предкрылки, кроме того, имеют щель подобно той, что используется в щеле

---

вых закрылках. Через эту щель воздух перетекает с нижней поверхности профиля на верхнюю, увеличивая при этом скорость потока , что повышает его устойчивость к отрыву.



- щиток Крюгера








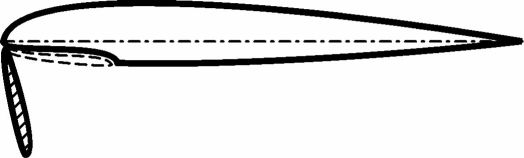
- отклоняемый носок









- предкрылок

Рис. 37. Средства механизации передней кромки крыла






На рис. 38 показано влияние механизации на коэффициент подъемной силы крыла.

---

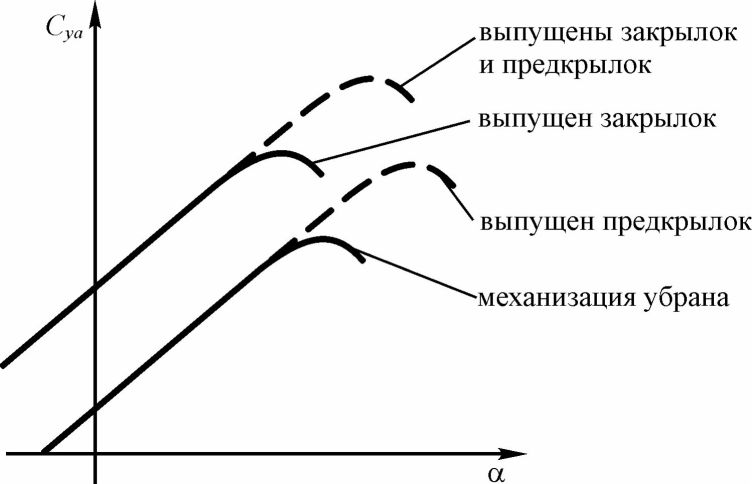
Рис. 38. Влияние механизации крыла на вид зависимости C_va = f (ос)

Кроме использования описанной выше механизации крыла для улучшения взлетно-посадочных характеристик самолета используются различные энергетические методы. Они основаны на использовании энергии

основных или вспомогательных силовых установок. Здесь может использоваться сжатый воздух, отбираемый от компрессора, струя воздуха, выдуваемая из сопла реактивного двигателя, а также воздух, отбрасываемый воздушным винтом. Эти мероприятия позволяют привнести дополнительную энергию в поток, что затягивает отрыв пограничного слоя на больших углах атаки. При этом также растет скорость потока, обдувающего крыло, что непосредственно увеличивает подъемную силу.

2. Основы динамики полета летательных аппаратов

Динамика полета - это наука о движении ЛА. Различают движение центра масс ЛА (траекторное движение) и движение ЛА вокруг его центра масс. К первому виду движения относятся горизонтальный полет ЛА, набор высоты, снижение, взлет, посадка, вираж и др. В процессе же движения вокруг центра масс ЛА может накреняться набок, задирать или опускать нос, поворачиваться влево или вправо, иными словами, ЛА может вращаться вокруг центра масс. При этом ЛА должен сохранять устойчивость своего положения в пространстве и обладать управляемостью.

Рассмотрим сначала траекторное движение, а затем перейдем к устойчивости и управляемости.

1. 
   Траекторное движение самолета
   

1. 
   Уравнения движения центра масс самолета
   

Самолет движется в воздухе под действием аэродинамической силы Ra , силы тяги двигателей Р и силы тяжести G. С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор Р обычно располагается в базовой плоскости самолета и образует некоторый угол с осью ОХ связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор Р приложен в центре масс.

Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.

Установившийся горизонтальный полет - это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39).

Уравнения движения центра масс самолета запишутся в этом случае следующим образом:

Pcos а = Х_а-,

Y_a + Psin a = G.

Поскольку угол атаки ос мал (при этом cos ос ® 1, a sin ос ® 0), то можно записать:


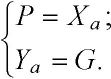
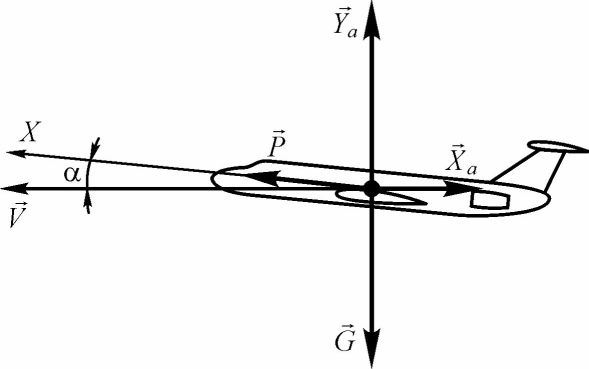
Рис. 39. Схема сил, действующих на самолет в установившемся горизонтальном полете
(49)

Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета Е_гп.

Учитывая, что G = mg (где т - масса самолета, a g - ускорение свободного падения), можно записать:

Cye^S^mg, (50)

откуда:

к (51)

Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха р (которая зависит от высоты полета),

площади крыла Л'_кр и коэффициента подъемной силы C_va. Поскольку C_va напрямую зависит от угла атаки ос, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.

Установившийся набор высоты - прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории 0, показана на рис. 40.



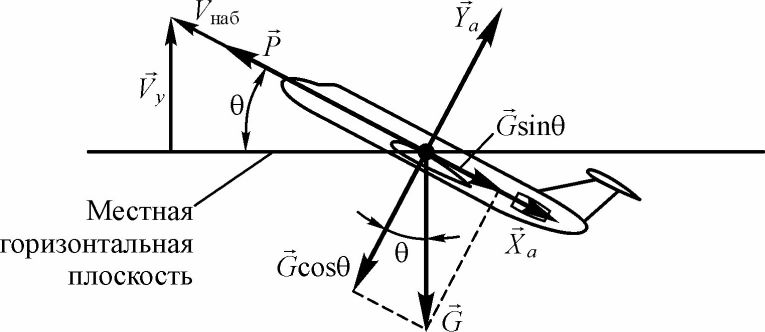
Рис. 40. Схема сил, действующих на самолет при установившемся наборе высоты (угол атаки принят малым и не показан)

В этом случае уравнения движения примут вид:

'Р = Х_а + G sin 0;

Y_a =G cos 0.

Необходимо отметить, что при наборе высоты тяга двигателей Р уравновешивает не только силу лобового сопротивления Х_а, как в горизонтальном полете, но и составляющую силы тяжести GsinO. Подъемная сила Y_a при этом требуется меньшая, поскольку GcosO < G.

Важной характеристикой самолета является его скороподъемность - вертикальная скорость набора высоты V_v. Из рис. 40 видно, что:

Vy=VHadSinO. (53)

Установившееся снижение - прямолинейное движение самолета вниз с постоянной скоростью. На рис. 41 показана схема сил, действующих на самолет при снижении.




Местная горизонтальная плоскость

Рис. 41. Схема сил, действующих на самолет при установившемся снижении (угол атаки принят малым и не показан)






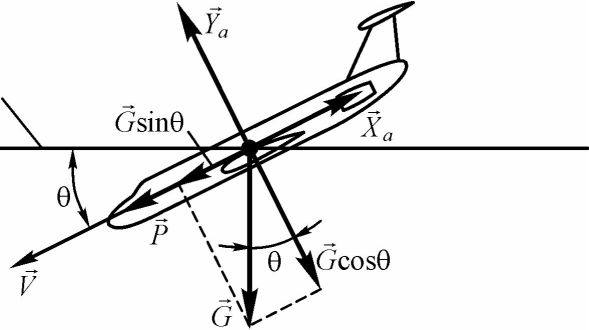
Уравнения движения для установившегося снижения имеют вид:

\Р = Х_а -Gsin9;

\ (54)

Y_a =G cos 9.

Если мы поделим первое уравнение системы (54) на второе, то получим:

tSd-^уУ (55)

Из уравнения (55) видно, что установившееся снижение возможно только, если тяга меньше лобового сопротивления (Р<Х_а). Обычно снижение происходит при малых значениях тяги (при тяге малого газа), поэтому можно принять, что Р

9. Такой режим полета называется планирование м . В этом случае:

---

Важной характеристикой является дальность планирования £пл с заданной высоты Япл- Легко видеть, что:

tg0 = Y⁵⁵-, (57)

^ПЛ

откуда:

Ь_ш=^=- = Н_ШК. (58)

tg9

Из формулы (58) видно, что чем выше аэродинамическое качество самолета, тем больше будет дальность планирования.

2. 
   Перегрузка
   

В авиации широко используется понятие перегрузки. Этим понятием удобно пользоваться как при решении задач динамики полета, так и при расчете самолета на прочность, а также в других случаях.

Перегрузкой называется сумма векторов всех сил, действующих на самолет, кроме силы тяжести, деленная на величину силы тяжести. В полете перегрузка равна:


(59)
- P + Ra
п =

mg

При посадке и движении по аэродрому в числитель дроби надо добавить силу реакции опоры.

Как видно из формулы (59) перегрузка - величина безразмерная. Однако иногда перегрузку ошибочно пытаются измерять величиной, представляющей собой произведение некоторого числа на ускорение свободного падения g, и говорят при этом, например: «Перегрузка равна 4g». Это неправильно. Грамотно будет сказать: «Перегрузка равна 4».

Перегрузка - величина векторная, т.е. кроме непосредственно величины она имеет направление и может быть отрицательной или положительной в зависимости от ориентации ее вектора относительно осей координат. Проекции перегрузки на оси скоростной системы координат равны:

PcosoccosB - Х_а


Однако чаще пользуются проекциями перегрузки на оси связанной системы координат. При малых значения углов атаки ос и скольжения Р можно считать, что:


(61)
М х М ха ->

Му М у_а ,

Эти проекции носят следующие названия:

п_х - продольная перегрузка;

n_v - нормальная перегрузка;

---

n_z - поперечная перегрузка.

Легко определить из формул (60) и (61), что, например, в установившемся горизонтальном полете на малом угле атаки:


(62)
n_x = O'
- n_y =1;

n_z = 0.

3. 
   Метод тяг Н.Е. Жуковского
   

При рассмотрении установившегося движения самолетов с турбореактивными двигателями для определения летно-технических характеристик самолета удобно пользоваться методом тяг, который разработал Н.Е. Жуковский. Метод тяг Жуковского основан на сравнении величин потребной и располагаемой тяг.

Потребной тягой Р_п называется тяга, необходимая для установившегося горизонтального полета на данной высоте с заданной скоростью. Она численно равна силе лобового сопротивления самолета:

Ри=Х_а. (63)

Располагаемая тяга Р_р- это максимально возможная суммарная тяга всех двигателей самолета на данной высоте и при данной скорости полета.

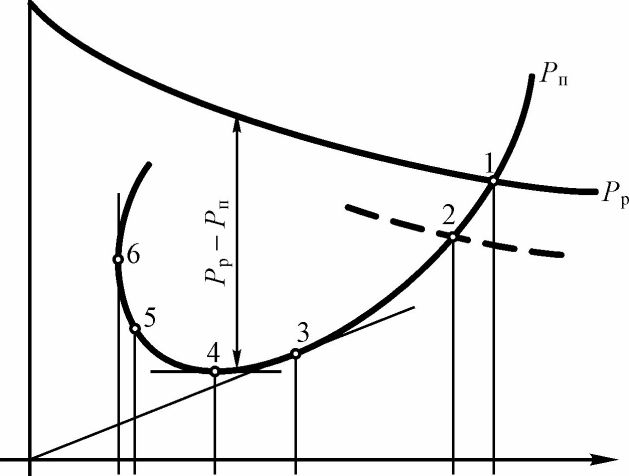
Сравнение потребной и располагаемой тяг удобно осуществлять, построив совмещенный график зависимостей Р_п и Р_р от скорости полета V для данной высоты полета и данной массы самолета (см. рис. 42). Такой график называется диаграммой потребных и располагаемых тяг. Рассмотрим характерные точки на этой диаграмме.


V ■ Е^д?^п V V -

^v min v _min^у нв у креис

V₂ P_max V

Рис. 42. Диаграмма потребных и располагаемых тяг



Точка «1», где пересекаются кривые потребных и располагаемых тяг, очевидно, соответствует режиму максимально возможной скорости установившегося горизонтального полета Е_111ах, т.к. при большей скорости полета потребная тяга будет превышать располагаемую. Точки же, лежащие на кривой Р_п =f(V) левее точки «1» (например, точка «2»), соответствуют установившемуся горизонтальному полету со скоростью, меньшей Е_111ах, в данном случае - со скоростью V^. Для осуществления такого режима полета необходимо несколько уменьшить тягу двигателя (см. кривую, выполненную штриховой линией) и увеличить коэффициент подъемной силы C_va. Не вдаваясь в подробности отметим, что летчик имеет возможность в полете управлять тягой двигателя и подбирать угол атаки, обеспечивающий требуемый C_va.

---