Оқушы қандай анықтамалармен, әдістермен және тұжырымдармен жұмыс жасайтынын жақсы түсіну үшін геометрия курсында біз геометрияның негізгі оқулықтарына, мұғалімге арналған оқу құралдарына және мұғалімдердің әзірлемелеріне талдау жасаймыз.

7-сыныпқа ерекше назар аударамыз, өйткені осы кезеңде курстың негізгі бағыттары анықталады.

8-сыныпқа арналған геометрия оқулығында критерий теоремасы ұғымы енгізіліп, осындай теоремалар мен дәлелдердің мысалдары егжей-тегжейлі сипатталған. Барлық әдістемелік желінің ерекшелігі-жаңа тақырыпты қайта зерттеу-бұл алдыңғы материалды қайталау , бұл балаларға жаңа материалды өз бетінше үйренуді жеңілдетуге мүмкіндік береді.

9-сыныпта оқушылар синус формуласы арқылы параллелограмның ауданы туралы теорема сияқты кейбір теоремалардың дәлелдерін өз бетінше шығаруы керек. Қосымша материал қазірдің өзінде теореманың құрылымын және оның дәлелдерін емес, пәндік материал туралы қосымша материалды қамтиды.

Осы курстардың әдістемелік ұсыныстарына жүгінейік. Бүкіл курстың міндеттерінің тұжырымдамасында дәлелдеуді оқытуға ерекше назар аударылмайды. Бірақ барлық 3 әдістемелік құралдарды талдағаннан кейін мұғалім балаларға жоғарыда көрсетілген әдістердің кез-келгенімен теоремаларды дәлелдеуге уақыт бөле алады деген қорытынды жасаймыз.

Геометрияның негізгі мәліметтері анықтама ретінде ұсынылады, содан кейін жауапты негіздеу қажет болатын тапсырма беріледі . Бұл таза түрдегі дәлел емес, бірақ логикалық негіздемесі бар, бұл оқушыларға геометриядағы әр анықтаманың дұрыстығын түсінуге мүмкіндік береді. Дәлел ұғымы бірінші тарауда енгізілген.

«Үшбұрыштардың теңдігі» тақырыбын зерттеу кезінде дәлелдемелермен қалай жұмыс істеу керектігі қысқаша сипатталған, бірақ аксиомаларды қалай қолдануға және оларды қандай ретпен жазуға баса назар аударылған, бірақ дәлелдеу кезінде қадамдардың ретін қалай анықтауға болмайды. Бұл теореманың өзін талдаудың шамамен жұмыс жоспарын және дәлелдердің мысалдарын, кейбір тұжырымдарды сипаттайды.

Әрі қарай, геометрия курсы бойынша 8 және 9 сыныптарда оқулықтың құрылымы сақталады, дәлелдер келтіріледі, оған дайын логикалық қорытынды мен негіздеме бар. Белгі немесе қасиет теоремасын тәуелсіз тұжырымдау үшін дәлелдеу тапсырмалары бар. Мысалы: « егер параллелограммда диагональдар тең болса, онда мұндай параллелограмм тіктөртбұрыш екенін дәлелдейміз».

---

Оқулықтың әдістемелік ұсыныстарына жүгінейік. Оларға көрсетілгендей, алғашқыда аксиоматикалық әдіс дәлелдемелер берілмейді. Дәлелдеу әдісі барлық геометрия оқулықтары үшін дәстүрлі-бұл үшбұрыштармен жұмыс. Дәлелдемелермен жұмыс өзара іздеу әдісіне немесе түсіндірме-иллюстрацияға негізделген.

8-сынып курсында үшбұрыштардың теңдік белгілерін қолдануға басты назар аударылады, ал балалар дәлелдерді өз бетінше жасай алады.

9-сыныпта геометрия бойынша 7 және 8-сыныптағы фактілерге сүйене отырып, тәуелсіз дәлелді негіздеу әдісі көбірек қолданылады.

Жасалған жұмысты қорытындылай келе, дәлелдемелермен жұмыс істеудің негізгі әдістері қолданылатындығын білуге болады. Алайда, әр оқулықта теореманың құрылымы, әсіресе онымен жұмыс істеу ережелері, дәлелдердің кезеңдері мен түрлері сипатталмайды. Сонымен, мұғалімнің басты міндеті – әр оқушыны теоремаларды негіздеу және дәлелдеу қабілетін үйрету.

Сабақта « қарама-қайшылықтан ойлау және дәлелдеу « жұмысты алгебрада немесе күнделікті өмірде кездесетін пайымдауларды дәлелдеуден бастайды. бұл тәсіл сізге негізгі тапсырманы қабылдауға мүмкіндік береді –оның ақиқатын әр пікірді тексеру.

Тағы бір тәсіл бар, онда оқушылар өздерінің гипотезаларын дәлелдеу қажеттілігін бастапқы кезеңде жұпта немесе топта жұмыс істей алады. Сонымен математика пәнінің мұғалімі жеке пәндерді тереңдетіп оқытумен өз әзірлемелерін осы әдіспен жариялайды.

7-сыныпта В.А.Смирнов, Е.А. Тұяқов геометрия сабағы

Сабақтың орны: «параллель түзулер» тақырыбындағы сабақ

Сабақтың түрі: жаңа материалды игеру сабағы.

Сабақтың мақсаты: оқушыларда қарама-қайшылықтан дәлелдеу және дәлелдеу әдісі туралы білімді қалыптастыру және іс-әрекеттің болжамды негізін қолдана білу

Жанама дәлелдеуді жүзеге асыру («қарама-қайшылықтан» дәлелдеу, яғни тезистің ақиқатын оған қайшы келетін ойдың жалғандығын (антитез) дәлелдеу арқылы анықтау.

Сабақ жоспары.

I. Ұйымдастыру сәті.

II. Білімді өзектендіру (білім алушыларды белсенді саналы меңгеруге дайындау).

Тақырыпты құрайтын ұғымдарды талдау (фронтальды қайталау)

Пайымдау-логикалық дәйекті түрде баяндалған белгілі бір тақырыптағы бірқатар ойлар, пайымдаулар, тұжырымдар. Ойлаудың мақсаты-тақырып немесе құбылыс туралы жаңа білім алу.

Пайымдау- айтылған шын немесе жалған ой, тұжырым [19,220 б.].

Дәлел – шындық дәлелденген басқа тұжырымдарды келтіру арқылы кез-келген тұжырымның ақиқатын анықтайтын дәлел. Дәлелдеудің мақсаты – кез-келген тұжырымның ақиқатын анықтау.

---

Сонымен, біздің мақсатымыз?

Мәлімдемелерді «қарама-қайшылық» дәлелдеуге үйрену.

2. Сергіту сәті.

Тапсырма: Қарама-қайшылық туралы айтып өтеміз (жауаптарды карталарға енгіземіз).

1. Геометрия пәнін 7-сыныпта оқи бастайды.

2. Бүгін жексенбі.

3. А саны жұп.

4. 135 саны 2-ге бөлінеді.

5. 25 саны тақ.

6. 48 саны тақ.

7. А саны 10-нан аз.

8. 5 саны 10-нан аз.

9. АВС үшбұрышы-тең қабырғалы.

10. Бұл тікбұрыш түзу.

11. Тікелей пропорционалдылық графигі шығу тегі арқылы өтеді.

(Нәтижелерді алдын-ала талқылау (слайд)

Қандай жағдайларда теріс мәлімдеменің шын немесе жалған екенін анықтауға болады?)

III. Жаңа білімді игеру кезеңі.

1. Мәселені белгілеу (әңгіме). (Жағдайлар ұсынылады)

Біріншісі: «қатты дауыл болды:

• 
  жел ағаштарды сындырды, шатырларды жұлып алды;
  
• 
  теңізде күшті толқындар пайда болды».
  

Сұрақ: бұл сөйлемде не айтылған? Автор өз пікірін қалай дәлелдейді? Қорытынды: дауылдың белгілері мәлімдеменің ақиқатын растайды.

Екінші: «Бұл зат магнит емес. Егер ол магнит болса, ол металл заттарды өзіне тартады».

Сұрақ: бұл сөйлемде не айтылған? Автор өз пікірін қалай дәлелдейді?

Қорытынды: авторда заттың магнит емес екенін көрсететін фактілер жоқ. Ол мұны тікелей дәлелдемейді. Керісінше болжайды: зат – магнит. Ойлау арқылы ол байқау мен магниттің қасиеті арасындағы қайшылыққа келеді. Бұл қайшылық оның болжамын жоққа шығарады. Фактіні жоққа шығару дұрыс емес болғандықтан, факт өзі дұрыс: зат магнит емес.

(Заттармен практикалық жұмыс: магнит және басқа заттар).

Сонымен. Мәселе: шындықты анықтау үшін (дәлелдеу үшін) тікелей фактілер жоқ жағдайлар бар.

1. Мәселені шешу: Қарама-қайшылықты ойлау арқылы (дәлелдеу). Мысалдар:

1). Үшбұрышта бірден көп емес тікбұрыш болуы мүмкін екенін дәлелдейміз.

(Егер үшбұрышта кем дегенде екі тікбұрыш болса, онда осы бұрыштарды үшінші тараппен құрайтын жақтар оған перпендикуляр болар еді. Бірақ содан кейін үшіншіге перпендикуляр екі түзу теоремасы бойынша бұл сызықтар параллель болады, яғни қиылыспайды және үшбұрыш құрмайды. Бұл үшбұрыш жағдайына қайшы келеді.

Біз дәлелдеуді қалыптастырамыз:

Үшбұрыштың бір тікбұрыштан артық болуы мүмкін емес екенін дәлелдейміз.

1. Мысалға үшбұрышта бір бұрыштан көп тікбұрыш бар деп алайық, мысалы, екі.

2. Сонда ... біз қайшылыққа келеміз…...............

3. Демек, біздің болжамымыз дұрыс емес, бірақ бұл дұрыс…...............

---

4. Фронтальды, ауызша (қарама-қайшылықтан ойлау (дәлелдеу) кезінде іс-қимыл жоспарын құру).

Қарама-қайшылықты дәлелдеу жоспары;

1. Қарама-қайшылықты дәлелдеу керек нәрсені болжау.

2. Белгілі фактілерге негізделген пайымдауды жүргізу.

Дәлелдерді басқа белгілі фактімен қарама-қайшылыққа келтіреміз.

3. Қорытынды жасау: болжам дұрыс емес, бірақ дәлелдеуге тура келді;

(оқушыларға «қарама-қайшы дәлелдеме» жадынамалар таратылады).

IV. Жаңа білім мен дағдыларды бекіту кезеңі.

1). (жұппен жұмыс, жұптарға карточкаларда тапсырмалар беріледі)

1. Сіз ХХ ғасырда дүниеге келмегеніңізді дәлелдеңіз.

2. 346 саны 3-ке бөлінбейтінін дәлелдеңіз.

3. 346 саны 5-ке бөлінбейтінін дәлелдеңіз.

4. 346 саны 9-ға бөлінбейтінін дәлелдеңіз.

5. 341 саны 2-ге бөлінбейтінін дәлелдеңіз.

6. Есептеу дұрыс жүргізілмегенін дәлелдеңіз: 536154523 * 2598563 =54276589321

7. Берілген нүктеден берілген сызыққа жүргізілген перпендикулярдың бірегейлігін дәлелдеңіз.

2). Параллель сызықтардың аксиомасының салдарын дәлелдеу үшін «қарама-қайшылықтан дәлелдеу» қолдану (фронтальды)

Аксиома: берілген сызықта жатпайтын нүкте арқылы берілген сызыққа параллель бір ғана сызық өтеді. ( жұппен жұмыс)

Қорытынды 1. Егер түзу екі параллель сызықтың біреуін кесіп өтсе, онда ол екіншісін кесіп өтеді. (Қарама-қайшылықты дәлелдеу»).

Бастау (шарт) ұсынылады, оған сәйкес оқушылар сурет салып, гипотеза – қорытынды ұсынады. (Бізде дәлелдеу үшін тікелей фактілер бар ма?

Ия, түзу екінші сызықты кесіп өтеді, өйткені...? Мұндай фактілер жоқ. Содан кейін біз қарама-қайшы дәлелдеуге тырысамыз…

Қорытынды 2. Егер екі сызық үшінші сызыққа параллель болса, онда олар параллель болады. («Қарама-қайшы дәлелі»)

V. Қорытындылау кезеңі.

1. Қарама-қайшы дәлел (пайымдау) қашан қолданылады?

3. Тәсілдің мәні неде?

4. Дәлелдеу жоспары?

5. Жаңа геометриялық фактілер?

Үй / тапсырмасы

Осылайша, біз геометрия сабағында мұғалімнің әдістемелік жұмысының негізгі әдістерін дәлелдедік, атап айтқанда:

• 
  Өзара іздеу
  
• 
  Түсіндірме иллюстрациялық
  
• 
  Өзіндік зерттеу
  

Сонымен қатар олар геометрия бойынша теоремалардың дәлелдерін оқытуда қандай ұғымдар бар екенін және олардың қалай ұсынылғанын анықтады. Сондай-ақ практик мұғалімдердің кейбір әдістемелік әзірлемелеріне назар аударды.


2.2 Геометрия курсында ұғымдар мен теоремаларды енгізу әдістемесі

---

Геометрия курсында ұғымдар мен теоремаларды енгізу әдістемесі бірқатар математикалық ұғымдар белгісіз. Погореловтың оқулығында оларға мыналар жатады: нүкте, түзу, түзуге жататын нүкте; « В нүктесі А және С нүктелерінің арасында жатыр»;

«жартылай жазықтық», «кесіндінің ұзындығы», «бұрыш өлшемі», «берілген өлшемнің кесіндісін(бұрышын) кейінге қалдыру». Анықталмаған ұғымдардың қасиеттері аксиомалармен сипатталады. Барлық басқа ұғымдар анықталған.

Кейбір анықтамалардың ерекшеліктерін атап өтеміз:

1. 
   кесінді ұштары оған жатпайтындай етіп анықталады; осыған байланысты белгілеуді шаршы жақшалар көмегімен пайдалануға болмайды;
   
2. 
   Жартылай түзу бастапқы нүкте оған тиесілі емес деп анықталады;
   
3. 
   бұрыш бұрыштың шыңы оған жатпайтындай етіп анықталады;
   
4. 
   үшбұрыштың шыңдары (бірақ анықталған) оған тиесілі
   

«Үшбұрыш дегеніміз-бір түзу сызықта жатпайтын үш нүктеден және жұптасып үш сегменттен тұратын фигура осы нүктелерді қосу. Нүктелер үшбұрыштың шыңдары, ал сегменттер жақтар деп аталады».

«Бұрыш - бұл бұрыштың жоғарғы нүктесінен және осы нүктеден шығатын екі түрлі жартылай түзуден тұратын фигура – бұрыштың жағы». Бүкіл геометрия курсының орталық тұжырымдамаларының бірі-тең үшбұрыштар ұғымы. Киселевтің оқулығында үшбұрыштардың теңдігі позиция арқылы анықталады.

Біз геометрияның жүйелі курсын 7-сыныпта аксиомалар түрінде тұжырымдалған қарапайым геометриялық фигуралардың негізгі қасиеттерімен танысудан бастаймыз. № 47, 23-бет AC және Sun қиылысады, яғни В нүктесі бір жарты жазықтықта, ал А нүктесі екіншісінде.



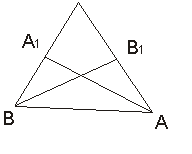
Сурет 2

В₁ (АС) нүктесі А және С нүктелерінің арасында орналасқан А₁ (ВС) нүктесі және В және С нүктелерінің арасында орналасқан (АА₁), содан кейін А және С нүктелері әр түрлі жартылай жазықтықтарға жатады, өйткені АС және В сегменттері қиылысады.

Сондықтан В және В₁ нүктелері (өйткені В₁ С және А арасында орналасқан) әр түрлі жартылай жазықтықтарда жатыр, сондықтан Aa₁ VV1 шешу кезінде жартылай жазықтық ұғымы және IV аксиома қолданылады. §1 оқылғаннан кейін оқушыларға ұғымдар беріледі: аксиомалар, теоремалар, дәлелдердің қарапайым формалары келтірілген.



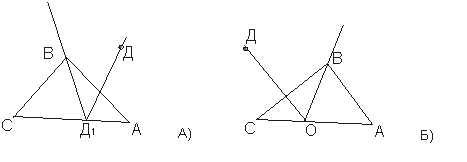
Сурет 3

Соған сәйкес ∆ АВС (СА) жақтарының бірі қиылысқандықтан, түзу қалған екеуінің бірін қиып өтеді. ДОА қарастырайық. Егер ДОА < АОВ, онда ОД сәулесі АО және ОВ сәулелерінің арасында орналасады, сондықтан АВ кесіндісін кесіп өтеді. Егер ДОА > ВОА, онда ОД сәулесі ВК кесіндісін кесіп өтеді (бұл мынадай жағдайларға байланысты: ВОА < ДОА және ОД сәулесі ОС және ОС сәулелерінің арасында жатыр. Үшбұрыштардың теңдік белгілерін зерттеу әдістемесі.

---

Смотрите также файлы

• Виды тестирования. Планирование тестирования.docx

• Министерство образования красноярского края кга поу канский педагогический колледж.docx

• Лекция Лагерная проза в русской литературе 2 половины хх века.docx

• 2. в 1972 году, Хироаки Аоки расширил свой бизнес и открыл новый ресторан Benihana на Беверли Хиллз в Калифорнии.docx

• Занятие при реализации основной или дополнительной образовательной программы.docx