Осылайша, біз теореманың пайымдау, растау екенін білдік. Өз кезегінде, мәлімдемелердің төрт түрі бар

1. 
   Жалпы пайымдау
   
2. 
   Жеке пайымдау
   
3. 
   Жалпы теріс
   
4. 
   Жеке теріс,
   

Теореманың өзі математикалық тұжырым болып табылады, оның ақиқаты дәлелдеу арқылы анықталады. Теорема құрылымында үш бөлік бар:

• 
  түсіндіру бөлімі;
  
• 
  шарт;
  
• 
  қорытынды.
  

Сонымен қатар, теоремаларды тұжырымдау кезінде пайымдаудың үш формасы қолданылатынын анықтадық:

• 
  категориялық;
  
• 
  шартты;
  
• 
  бөлу.
  

1.2 Математикалық теоремаларды дәлелдеу әдістері
Оқушылардың дәлелдеу қабілетін қалыптастырудағы негізгі жүктемені геометрия курсы көтереді. Д. Поя геометриялық жүйені құру кезінде дәлелдердің маңызды рөлін атап өтті: «геометриялық жүйе дәлелдермен негізделген. Әр теорема алдыңғы аксиомалармен, анықтамалармен және теоремалармен кейбір дәлелдермен байланысты. Мұндай дәлелдерді түсінбестен, жүйенің мәнін түсіну мүмкін емес».

Логикалық сөздікте бұл термин келесідей анықталады : қорытынды дегеніміз – бір немесе бірнеше пайымдаулардан қорытынды немесе нәтиже деп аталатын жаңа пайымдау логикалық түрде алынған пайымдау.

Теоремаларды дәлелдеудің жеке және жалпы әдістері бар. Дәлелдеудің жеке әдістеріне геометриялық қайта құру әдісі, векторлық, координаталық, алгебралық әдістер және т. б. кіреді, бірақ бұл жұмыста біз мектептегі математика курсында жиі кездесетін жалпы әдістерге, атап айтқанда синтетикалық, аналитикалық әдістерге (төмен және жоғары талдау), қарама-қайшылықтың дәлелі және т. б.

Мектеп геометрия курсындағы теоремаларды дәлелдеудің барлық әдістерінің ішінде синтетикалық әдіс негізгі жүктемені көтереді, өйткені ол кез-келген басқа әдіспен дәлелдеудің ажырамас бөлігі болып табылады.

Математикалық сөйлемнің дәлелі синтетикалық деп аталады, егер ол келесі логикалық схема бойынша жүзеге асырылса: мұндағы Т-осы сөйлем дәлелденетін және B1(x), B2(x), жататын ұсынылған математикалық теорияның белгілі бір жиынтығы. Дәлелдемені құрайтын Вп(х), сондай-ақ А(х) және В(х) пайымдаулары.

Осылайша, теореманы дәлелдеудің синтетикалық әдісінде силлогизмдер тізбегі ой теореманың жағдайынан оның тұжырымына ауысатын етіп құрылады.

---

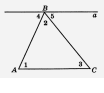
Сурет 1
«Үшбұрыштың ішкі бұрыштарының қосындысы туралы» теореманың синтетикалық дәлелін қарастырамыз.

Аналитикалық әдіс: дәлел іздеген кезде ой теореманың қорытындысынан оның жағдайына ауысады. Бұл әдістің артықшылығы-дәлелдеудің бастапқы буыны бар, қосымша құрылымдар ынталандырылады, оқушылардың шығармашылық белсенділігі артады. Кемшіліктер-үлкен уақыт жоғалту, жасанды қосымша құрылыстарды негіздеу қиын.

Үшбұрыштың бұрыштарын табамыз, оның екі шыңы бар сыртқы бұрыштар 110° және 140°екенін біліңіз.

Үшбұрыштағы жағдайға сәйкес біз тек екі сыртқы бұрышты білеміз. Бірақ сыртқы бұрыштың осы шыңмен ішкі бұрышқа жақын екенін және іргелес бұрыштардың қосындысы 180° екенін біле отырып, үшбұрыштың екі ішкі бұрышын оңай табуға болады. Содан кейін үшбұрыштағы бұрыштардың қосындысы туралы теорема бойынша біз үшінші бұрышты табамыз.

Шешімі.

Мұғалім: тапсырмада бізге не берілген?

Балалар: бізге сыртқы екі бұрыштары 110° және 140°болатын үшбұрыш берілген.

Мұғалім: егер бұл сыртқы бұрыштар болса, олар туралы не айтуға болады?

Балалар: Сыртқы бұрыш сол жоғарғы жағында ішкі бұрышқа іргелес.

Мұғалім: іргелес бұрыштар туралы не білеміз?

Балалар: іргелес бұрыштардың қосындысы-180°. Сонымен, біз b және C: B мәндерін таба аламыз= 180° – 110° = 70°, C = 180° – 140° = 40°.

Мұғалім: Жарайды, енді біз үшбұрыштың екі бұрышын білеміз. Үшінші бұрышты қалай табуға болады

Балалар: үшбұрыштың бұрыштарының қосындысы туралы теорема бойынша А жолын табамыз.

А + В әрпі + С = 180°, содан кейін А = 180° - (В + С әрпі),

А = 180° – (40° + 70°) = 70°.

Жауап: 70 ° және 40°.

Математиканы оқытуда синтетикалық әдіс маңызды орын алуы керек. Оқытуды оқушылар синтетикалық әдісті қолдануды үйреніп қана қоймай, оның мәні мен ерекшеліктерін түсінетін етіп жүргізу керек, өйткені оны игеру адамның практикалық іс-әрекетінде өте маңызды. Дәлелдердің синтетикалық мәлімдемесі толық және қысқа. Алайда, осы стильде математиканың барлық сабақтарын жүргізу тиімсіз. Бұл, ең алдымен, математиканы жаңадан бастаушылар үшін синтетикалық дәлелдер түсініксіз болып көрінетіндігіне байланысты.

Кез-келген аналитикалық дәлел синтетикалық және керісінше болады. Бұл оқу процесінде кеңінен қолданылады. Технология келесідей болуы мүмкін:

1) синтетикалық дәлел оның жоспарын аналитикалық іздеуден бұрын болады;

2) синтетикалық дәлелдеме талдамалық дәлелдемемен ауыстырылады, үй тапсырмасы ретінде – оқулық бойынша синтетикалық дәлелдемені зерделеу;

---

3) дәріс әдісін қолдану кезінде (негізінен негізгі мектеп курсынан тыс) таза синтетикалық дәлелдеу әдісі жиі қолданылады.

Математикалық индукция әдісінің геометрияда таралуы жоқ, өйткені ол натурал сандар жиынының қасиеттеріне негізделген, негізгі мектептен тыс, сондықтан біз оны арнайы зерттеуге жібермейміз.

Жанама дәлел: теореманың ақиқаты теоремадағы кейбір пайымдауларды жоққа шығару арқылы анықталады.

Планиметрия курсында ең көп таралған және жалғыз қолданылатын жанама әдісі-бұл дәлелдеу.

Қарама-қайшылықтан әдістің логикалық-математикалық мәні: тікелей теореманың орнына керісінше дәлелденеді .

Планиметрия теоремаларын дәлелдеудің осы негізгі математикалық әдістерінен басқа неғұрлым нақты әдістер туралы айтуға болады: симметрия әдісі, векторлық әдіс, алгебралық әдіс, ұқсастық әдісі, координаталық әдіс және т. б.

Қорытындылардың екі негізгі түрі бар – индукция және дедукция.

Индукция-бұл бір немесе бірнеше жеке пайымдаулардан жаңа жалпы шешім қабылданатын қорытынды. Индукцияның екі негізгі түрі бар – толық емес және толық.

Толық емес индукция-бұл бір немесе бірнеше жеке пайымдауларды қарастыруға негізделген қорытынды.

Толық индукция-бұл жағдайға қатысты барлық жеке пайымдауларды қарастыруға негізделген қорытынды.

Толық индукция негізінде жасалған қорытынды өте сенімді, толық индукция логикалық дәлелдеу әдісі болып табылады. Алайда, бұл әдіс келесі себептерге байланысты сирек қолданылады:

1. 
   қиындық,
   
2. 
   шексіз көп болғандықтан, барлық жеке және жеке пайымдауларды қарастырудың мүмкін еместігі.
   

Алайда, толық индукцияны қолдану мысалдарын келтіруге болады: жазылған бұрышты өлшеу туралы мәселені зерделеу кезінде барлық мүмкін жағдайлар қарастырылады:

1. 
   бұрыштың бір жағы – шеңбердің диаметрі;
   
2. 
   диаметр жазылған бұрыштың жақтары арасында жатыр;
   
3. 
   диаметр бұрыштан тыс.
   

Дедукция-бір жалпы пікірден және бір жеке пікірден жаңа шешім алынған қорытынды.

Осылайша, дедукцияның мәні-бұл ерекше жағдай жалпы жағдайға келтіріледі.

Шегеру(дедукция) -логикалық дәлелдеудің негізгі әдісі.

Теоремалардың дедуктивті дәлелі қадамдардың логикалық реттілігімен, негіздемелердің міндеттілігімен және олардың сенімді деп танылған математикалық фактілерге сілтемелерімен сипатталады.

Теоремаларды дәлелдеудің негізгі әдістерін анықтай отырып , дәлелдеудің дәлелдері тікелей және жанама болып бөлінеді деген қорытынды жасауға болады. Айта кету керек, тікелей дәлелдер үшін теоремаларды дәлелдеудің қолданылатын әдістері қолданылады:

---

• 
  Синтетикалық әдіс:
  
• 
  Аналитикалық әдіс
  
• 
  Математикалық индукция әдісі
  

Ал жанама дәлел үшін:

• 
  теоремаларды дәлелдеудің математикалық әдістері.
  
• 
  геометриялық түрлендіру әдісі:
  
• 
  үшбұрыштардың теңдігі мен ұқсастығы әдісі
  
• 
  шегеру әдісі
  

---

2. ТЕОРЕМАЛАРДЫ ДӘЛЕЛДЕУДІ ОҚЫТУДЫҢ ӘДІСТЕМЕЛІК ЕРЕКШЕЛІКТЕРІ
2.1 Теоремалармен жұмыс кезеңдері. Теоремаларды дәлелдеу тәсілдері

Геометрия курсында теоремаларды зерттеген кезде әр оқушыға екі тапсырма беріледі, бұл геометриялық объектінің жаңа қасиетін немесе белгісін немесе бірнеше объектілердің байланысын білу ; сонымен қатар ұсынылған тұжырымдардың ақиқатын логикалық негіздеу.

Екінші оқу мәселесін шешу үшін барлық жұмысты теоремалармен кезеңдерге бөлу керек .

Бұл жұмыста біз В. А. Смирнованың тәжірибесіне сүйенеміз. Мұғалім теоремаларды зерттеудің келесі кезеңдерін анықтайды:

• 
  Теореманы оқуға ынталандыру.
  
• 
  Теоремада көрсетілген фактімен танысу.
  
• 
  Теореманы тұжырымдау және теорема тұжырымындағы әр сөздің мағынасын түсіндіру.
  
• 
  Теореманың мазмұнын ассимиляциялау;
  
• 
  Теорема тұжырымын жаттау;
  
• 
  Оны дәлелдеу тәсілдерімен танысу;
  
• 
  Теореманы дәлелдеу;
  
• 
  Теореманы қолдану;
  
• 
  Теореманың бұрын зерттелген теоремалармен байланысын орнату.
  

Кез-келген геометриялық теореманы зерттеудің осы әмбебап алгоритмін біле отырып, дәлелдемелермен жұмыс істеу қиын болмайды.

Әрине, теоремаларды дәлелдеудің негізгі әдістерін есте ұстаған жөн. Әр әдіс, өз кезегінде, оқушының материалды түсінуін қамтамасыз етеді. Мұндай тәсілдерді В. А. Далингердің «оқушыларды теоремаларды дәлелдеуге үйрету» еңбектеріңізде көрсеткен. Оларды егжей-тегжейлі қарастырамыз:

Әдіс 1. Өзара іздеу әдісін қолдану, мұғалімнің оқушылармен жүргізетін эвристикалық әңгіме арқылы жүзеге асырылады. Айта кету керек, дәлелдер аналитикалық-синтетикалық әдіске сәйкес келуі керек.

Әдіс 2. Мұғалім теореманың дәлелі туралы түсіндіреді бірақ ол оқушыларға тікелей әсер етпейді. Түсіндірме және иллюстрациялық әдіс оқушыларға логикалық ойлау арқылы ойдың дұрыс бағытын көруге мүмкіндік береді. Бұл әдісті жиі қолдануға болмайды, өйткені түсіндіру кезінде дәлелдеу ұзаққа созылса, оқушылар ұзақ уақыт назар аудара алмайды, олар шаршай бастайды. Бұл әдістің ең маңызды «кемшілігі» - оқушылар қазіргі уақытта белсенді емес, яғни бұл әдісті ұзақ уақыт қолданған кезде барлық жаттығулар тиімді болмайды.

Әдіс 3. Оқулықты қолдана отырып, теореманы дәлелдеуді дербес зерттеу әдісі. Мұндай түсіндірмедегі мұғалім тек кеңесші ретінде әрекет етеді, ал негізгі жүктеме оқушыларға түседі. Алайда, егер жұмыс оқулықпен бірге жасалса, онда бұл әдіс екінші әдіске ұқсас болады, онда балалар дәлелдердің дұрыс талдауын талдайды, содан кейін ұқсастықпен дәлелдейді. Сонымен қатар, оқушыларға тұтас сызба дәлелдеу теоремаларын өз бетінше құрып, бүкіл тәртібін талқылау және құрастыру қажет.

---

Смотрите также файлы

• Виды тестирования. Планирование тестирования.docx

• Министерство образования красноярского края кга поу канский педагогический колледж.docx

• Лекция Лагерная проза в русской литературе 2 половины хх века.docx

• 2. в 1972 году, Хироаки Аоки расширил свой бизнес и открыл новый ресторан Benihana на Беверли Хиллз в Калифорнии.docx

• Занятие при реализации основной или дополнительной образовательной программы.docx