Үшбұрыштардың теңдігі туралы сұрақтарды ұсыну көбінесе тең үшбұрыштардың анықтамасын таңдауға байланысты. А. В. Погореловтың оқулығында үшбұрыштардың теңдігінің Гильберт анықтамасы келтірілген, ол алты теңдіктің орындалуын талап етеді: үшбұрыштардың сәйкес жақтары үшін үш және осы үшбұрыштардың сәйкес бұрыштары үшін үш. Тең үшбұрыштар тақырыбын ұсынудың тағы бір нұсқасын қарастырыңыз:

1. Екі үшбұрыштың теңдігі үшін (анықтамасы бойынша) осы үшбұрыштардың үш тиісті жағының равенттерін талап етеміз;

2. Аксиома ретінде біз келесі тұжырымдарды қабылдаймыз: "егер бір үшбұрыштың екі жағы мен олардың арасындағы бұрыш сәйкесінше екі жағына және олардың арасындағы басқа үшбұрыштың бұрышына тең болса, онда мұндай үшбұрыштар тең болады". Бұл тәсіл үшбұрыштардың теңдігінің үшінші белгісін дәлелдемеуге мүмкіндік береді және үшбұрыштар теңдігінің I белгілері (бұл аксиома), бұл теориялық материалдың қысқаруына және "үшбұрыштардың теңдігі" тақырыбының логикалық құрылымын жеңілдетуге әкеледі, дәстүрлі синтетикалық геометрияның негізгі әдістерінің бірін-тең үшбұрыштар әдісін ең қысқа жолмен енгізуге мүмкіндік береді.

Үшбұрыштар теңдігінің алғашқы белгісін зерттеу әдістемесі. А. В. Погореловтың әдістемелік схемасы:

1. Тиісті жақтардың екі жұбы және олардың арасында орналасқан бұрыштар тең екі үшбұрыш салу;

2. Алынған сурет негізінде оның шарты мен қорытындысын жазу үшін теореманы тұжырымдаңыз;

3. Дәлелдеу идеясын хабарлау;

4. Дәлелдеме жоспарын хабарлау;

5. Оның қадамдарын нақты айқындаумен дәлелдеме жүргізу;

6. Оның дәлелдемелерін бекітуді жүзеге асыру;

7. Оқушылармен белгілерді қолдана отырып, тапсырмаларды қарастырыңыз.

2.3 Планиметрия курсын оқытуда теоремалармен жұмыс істеуге арналған әдістемелік ұсынымдар
Алдыңғы параграфты талдай отырып, теореманың құрылымына және оның дәлелдеріне арналған материалдар жеткіліксіз екендігі белгілі болды. Әдістемелік жұмыстың негізгі бөлігі мұғалімге жүктеледі. Сондықтан планиметрия курсында кейбір негізгі теоремалардың мысалдарын талдаймыз

Алдымен теоремаларды дәлелдеудің негізгі ережелерін анықтауымыз керек.

1. 
   Теоремаларды дәлелдеу ережелері. Оқушылардың теоремаларды дәлелдеу қабілетін дамыту үшін:
   
2. 
   Дәлелдеуде қолданылатын бұрын зерттелген материалды оқушылармен қайталаймыз.
   
3. 
   Теореманы дәлелдемес бұрын, барлық оқушылар теореманың мазмұнын дұрыс түсінгеніне, теореманың шарты мен тұжырымын нақты түсінгеніне көз жеткізіңіз.
   
4. 
   Дәлелдеуді бастамас бұрын, мұғалім оқушыларды дәлелдеудің қажеттілігіне сендіруі керек.
   

---

Оқушылар дәлелдеу процесінде біз шынайы дәлелдерді (ұсыныстарды), бұрын дәлелденген теоремалар мен салдарларды, аксиомалар мен анықтамаларды қолданатынымызды жақсы түсінуі керек, сондықтан ауызша дәлелдеу қажет

1. 
   Дәлелдеуге көмектесетін дұрыс сызбаның болуын қадағалаңыз.
   
2. 
   Дәлелдеменің әрбір компонентін пысықтау.
   
3. 
   Дәлелдеу процесінде теореманың шарты толығымен қолданылуы керек. Бұл көбінесе оқушыларды ұмытып кеткен кезде дәлелдеуді жалғастыруға көмектеседі.
   

Дәлелдеу кезінде анықталған тұжырымдаманы оны анықтамамен алмастырған жөн. Дәлел өзгерген кезде пайымдау сипатына сәйкес келетін анықтаманы қолданыңыз (егер сіз квадраттың диагональдары арасындағы бұрышқа қызығушылық танытсаңыз, онда квадрат – ромб, егер диагональдардың ұзындығы болса, онда квадрат – тіктөртбұрыш).

Анықтама көбінесе анықталған тұжырымдаманың қажетті және жеткілікті белгісімен ауыстырылады.

Дәлелдемелердің формализмін (ресми есте сақтау) жеткілікті білместен болдырмау үшін, басқа белгілермен өзгертілген сызбада теореманың дәлелдемесін қайталау қажет.

Біз бұл жұмыстың орындалуын мысалмен көрсетеміз.

Теорема

Түзу сызықта жатпайтын нүктеден осы сызыққа тек бір перпендикуляр сызуға болады.

Алдымен сәуленің, кесіндінің, перпендикулярдың, іргелес бұрыштардың анықтамасын қайталау керек, теңдіктің алғашқы белгісі.

Сәуле-басы бар, бірақ соңы жоқ немесе берілген нүктеден және оның бір жағында орналасқан барлық нүктелерден тұратын түзу сызық.

Сегмент-түзудің шектеулі бөлігі.

Перпендикуляр - бұл сызықты дұрыс бұрышпен кесіп өтетін түзу.

Іргелес бұрыштар-екі бұрыш, олардың бір жағы ортақ, ал қалған екеуі бір-бірін түзу сызыққа дейін толықтырады. Екі іргелес бұрыштың қосындысы-180.

Үшбұрыштар теңдігінің алғашқы белгісі. Егер бір үшбұрыштың екі жағы мен олардың арасындағы бұрыш сәйкесінше екі жаққа және екінші үшбұрыштың арасындағы бұрышқа тең болса, онда мұндай үшбұрыштар тең болады.

Енді теореманы тұжырымдауға оралып, оның құрылымын анықтау керек.

Бұл теоремада нүкте мен түзу деген шарт анықталады, нәтиже-жалғыз перпендикуляр сызуға болады. Бұл кезеңде әр оқушы қолданылатын анықтамалар мен олардың арасындағы байланыстарды түсінетініне көз жеткізу керек.

Біз оны қалай дәлелдейтінін анықтаймыз, бірнеше әдістер бар. Біз әдісті үшбұрыштардың теңдік белгісі арқылы таңдадық.

Әрі қарай, біз геометриялық құрылым әдісін қолданамыз . Біз сәуле түсіреміз. Содан кейін ӘК сәулесінен АВС бұрышына тең СВD бұрышын кейінге қалдырамыз. ВD сәулесінде ВА кесіндісіне тең ВК кесіндісін кейінге қалдырамыз.

---

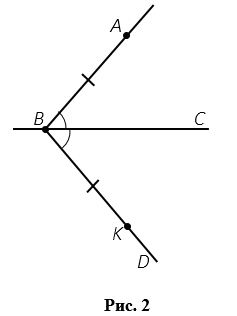
Сурет 4

АК түзу сызығын сызамыз, Н - нүктесі АК және ВСсызықтарының қиылысу нүктесі болсын.


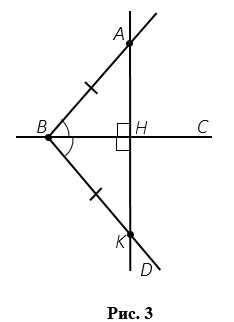
Сурет 5

АВН = үшбұрыштар теңдігінің бірінші белгісі бойынша КВН: ВН - жалпы жағы, ВА = ВК, ВН =КВН (салу бойынша), ВНА =ВНО. Бірақ ВНА және ВНО іргелес бұрыштар, содан кейін іргелес бұрыштардың қасиеті бойынша ВНА +HD = 180°, демек, іргелес бұрыштардың әрқайсысы түзу, яғни ВНЕ =DID = 90°, демек, барлық

Біз оның шынымен перпендикуляр екенін дәлелдедік, енді оның жалғыз екенін дәлелдейміз.

А нүктесі арқылы ӘК түзуіне тағы бір АН1 перпендикулярын салуға болады делік, онда ӘК түзуіне перпендикуляр екі АН және АН1 түзулері А нүктесінде қиылысады деп аламыз.



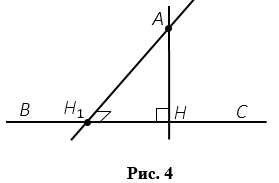
Сурет 6

Перпендикуляр түзулердің АН және АН₁ түзулері қиылыспайды, яғни біздің болжамымыз дұрыс емес және А нүктесі арқылы түзу ВС-ге бір ғана перпендикуляр сызуға болады. Теорема дәлелденді.

Әрі қарай, сіз кері теореманы өз бетіңізше тұжырымдай аласыз немесе дәлелдерді басқа жолмен таба аласыз. Мысалы:

А — түзу сызықта жатпайтын нүкте болсын. Алдымен А нүктесінен түзу сызыққа перпендикуляр сызуға болатындығын дәлелдейміз.

18-суретте көрсетілгендей АВС бұрышына тең МВС бұрышын ВС сәулесінен кейінге қалдырамыз, А. АВС және МВС бұрыштары тең болғандықтан, олардың біріншісін ВА және ВС бірінші бұрышындағы ВМ және ВС екінші бұрышының жақтарымен үйлесетіндей етіп екінші бұрышқа салуға болады.

Көрнекі түрде, бұл қабаттасуды суретте ВС түзу сызықта бүгілуі ретінде елестетуге болады. Бұл жағдайда А нүктесі ВМ сәулесінің А₁ нүктесімен сәйкес келеді.

AА₁ және ВСсызықтарының қиылысу нүктесін Н әрпімен белгілейміз. АН кесіндісі ВС түзуіне қажетті перпендикуляр болып табылады. Шын мәнінде, көрсетілген қабаттасу кезінде (суреттің бүгілуі) сәуле сәулемен біріктіріледі1 сондықтан НА1 бұрышы НА2 бұрышпен біріктіріледі. Демек, ∠1 = ∠2. Бірақ 1 және 2 бұрыштары іргелес, яғни олардың әрқайсысы түзу. Сонымен, АНмен ВС перпендекуляр.


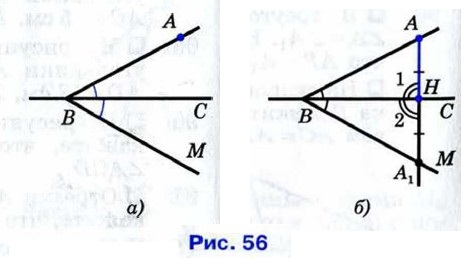
Сурет 7

Енді А нүктесінен түзу ВС-ге тек бір перпендикуляр сызуға болатындығын дәлелдейміз.

---

Егер А нүктесі арқылы ВС түзуінің АН₁К тағы бір перпендикулярын жүргізуге болады деп болжасақ, онда ВСтүзуіне перпендикуляр екі АН және АН₁ түзулері қиылысады. Бірақ бұрын геометрия курсында бұл мүмкін емес екендігі дәлелденді. Сонымен, А нүктесінен түзу сызыққа тек бір перпендикуляр сызуға болады. Теорема дәлелденді.



Осылайша , біз кез-келген әдіспен қолдануға болатын және кез-келген сабақта қолдануға болатын 7-ші геометрия сыныбының теоремасына дәлел мысалын қарастырдық. Біз жұмыстың негізгі әдістері мен теореманы дәлелдеумен жұмыс істеу ережелерін тұжырымдадық

---

ҚОРЫТЫНДЫ
Бұл курстық жұмыста тақырыптың негізгі ұғымдарына, теоремалардың тұжырымдарына, теоремаларды дәлелдеудің негізгі әдістеріне қатысты сұрақтар қамтылды.

Жұмысты талдай отырып, талдау дәлелдемелерді зерттеудің ең оңтайлы әдісі деп қорытынды жасауға болады.

Біз оқушылармен теоремада маңызы бар тұжырымдаманы қалпына келтіру қажеттілігімен байланысты жұмыс жүргізу керек екенін білдік. Оқушыларға мектеп оқулықтары мен әдістемелік әдебиеттерде кездесетін бірдей теореманың әртүрлі тұжырымдарын көрсету орынды екеніне көз жеткіздік.

Геометрияны, атап айтқанда дәлелдерді оқытуда әдістер жүйесін қолдану қажет. Олар мәтінді түсініп, мәселені тұжырымдап, үлгіні бөліп, зерттеу жүргізіп, барлық анықталған көзқарастар мен фактілерге күмәндануы керек.

Сондай-ақ, талдау және синтез сияқты жалпы дәлелдеу әдістерін қолдану студенттердің әр қадамды негіздеу қажеттілігін дамытудың ең сәтті құралдарының бірі болып табылатындығын анықтады. Мұндай жаттығумен алғашқы танысу айтарлықтай уақытты қажет етеді. Мұндай сабақ әсер етуі үшін мұғалім әр қадамды ойластырып, мектеп оқушыларын бір сатыдан келесі сатыға өткізуі керек, оқушылардың ойлары дұрыс бағытта жүруін қамтамасыз етуі керек, сондықтан олардың назарынан тыс қалмауы керек, бастысы, барлық сабақ үлгерімі төмен оқушыларда жаңа сабақты игеруге күш салатын болады. Әрине, сіз әрдайым оқушылардың белсенділігін қолдана алмайсыз, бірақ бұл жерде оқушылардың терең қызығушылығы байқалады, логикалық ойлау дамиды, танымдық белсенділігі артады.

Дәстүрлі-синтетикалық аспектілер геометрияда жетекші орын алады, қалған материалдарды ұсынуға негіз болады, оқушылардың кеңістіктік көрінісі мен қиялын қалыптастыруға ықпал етеді (дәстүрлі синтетикалық геометрияның кейбір бөлімдері(параллелизм, түзулер мен жазықтықтардың перпендекулярлық, үшбұрыштың қаттылығы) «құрылым геометриясы» деп аталады).

Тақырыптарға:

• 
  параллель және перпендикуляр түзулер, үшбұрыштардың теңдік белгілері, теңқабырғалы мен тең жақты үшбұрыштардың қасиеттері, үшбұрыштың жанында сипатталған шеңбер (үшбұрышқа жазылған), құрылыс міндеті;
  
• 
  төртбұрыштар, тұрақты көпбұрыштар, біз дәстүрлі түрде максималды білім беру мақсаттарын қоямыз, оларда жүйелі геометрия курсының басталуын көруге болады.
  

Координаталық-векторлық әдіс дәстүрлі синтетикаға көмекші математикалық әдіс ретінде қарастырылады. Көмекші әдіске дайындық оқушыларды координаталық немесе векторлық-координаталық әдіспен есептерді шешудің

---

Смотрите также файлы

• Виды тестирования. Планирование тестирования.docx

• Министерство образования красноярского края кга поу канский педагогический колледж.docx

• Лекция Лагерная проза в русской литературе 2 половины хх века.docx

• 2. в 1972 году, Хироаки Аоки расширил свой бизнес и открыл новый ресторан Benihana на Беверли Хиллз в Калифорнии.docx

• Занятие при реализации основной или дополнительной образовательной программы.docx