ек = 0,5hн = 0,5∙1500 = 0.75 м;

Мmax = ек Dmax = 0.75∙2538,5 = 1901,60 кНм;

Мmin = ек Dmin = 0.75∙714,3 =535,70 кНм.
Горизонтальная сила от мостовых кранов, передаваемая одним колесом:


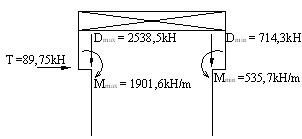
Рис.5. Нагрузки от мостовых кранов
ТКн = 0,05(9,8Q + GТ)/n0 = 0,05(9,8∙125 + 430)/4 = 20,69 кН
Расчетная горизонтальная сила Т, передаваемая подкрановыми балками на колонну от сил ТК:
Т = γнnnc∑ Тkн y = 0,95∙1,1∙0,85∙20,69∙4,884 = 89,75кН
Считаем условно, что сила Т приложена в уступе колонны.

Ветровая нагрузка.

Нормативный скоростной напор ветра q 0 = 0,27 кПа. Тип местности – А. Коэффициенты k для 10м – 1; 20 м – 1,25; 30 м – 1,4.

Расчетная линейная ветровая нагрузка, передаваемая на стойку рамы:

c – аэродинамический коэффициент;

с = 0,8 – с наветренной стороны; с = 0,6 – со стороны отсоса;

n – коэффициент перегрузки, n = 1,2;

В – ширина расчетного блока.

Линейная распределенная нагрузка при высоте:
до 10 м: 2,95∙1 = 2,95 кН/м;

20 м: 2,95∙1,25 = 3,69 кН/м;

30 м: 2,95∙1,4 = 4,13 кН/м.

22,6 м: 3,79 кН/м;

25,75 м : 3,94 кН/м.
Сосредоточенные силы от ветровой нагрузки:

Эквивалентные линейные нагрузки:



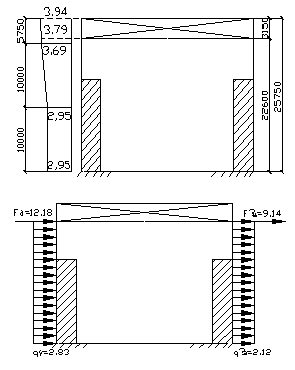
Рисунок 6 – ветровая нагрузка
2.3 Статический расчет поперечной рамы
Расчет на постоянные нагрузки. Основная система приведена на рис. 3, а, а схема нагрузки – на рис. 4,5. Сосредоточенный момент из-за смещения осей верхней и нижней частей колонны:
= - (331,8+254,66) ∙0,25 = -146,62 кН∙м
Параметры по табл.12.4 :
=1/5=0,2; =6,4/22,6=0,28 ≈ 0,3
Каноническое уравнение левого узла

Моменты от поворота узлов на угол φ = 1(M1):

---

Моменты от нагрузки на стойках (Mр):
=0,353∙(-146,62)= - 51,76 кН∙м

= - 0,145∙(-146,62)=21,26 кН∙м

= - 0,695∙(-146,62)= 101,90 кН∙м

=( - 0,695+1) ∙(-146,62)= -44,72 кН∙м
Моменты на опорах ригеля (защемленная балка постоянного по длине сечения)
/12 = - 22,12∙302 /12 = - 1659 кН∙м
Коэффициенты канонического уравнения:



Угол поворота
=1680,26 / 7,085i = 237,16 / i.
Моменты от фактического угла поворота (М1φ):








Эпюра моментов от постоянной нагрузки:









Проверкой правильности расчета служит равенство моментов в узле В (-228,9 =-228,9), равенство перепада эпюры моментов в точке С (156,7-10,04= 146,66), внешнему моменту (146,62 кН), а также равенство поперечных сил на верхней и нижней частях колонны

---

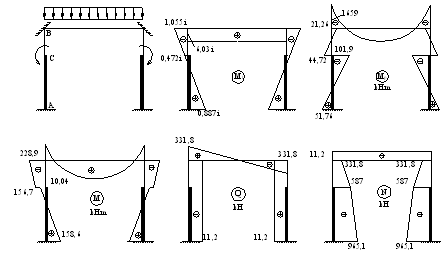
Рис. 7. Эпюры усилий в раме от постоянной нагрузки

Расчет на нагрузку от снега.

Проводится аналогично расчету на постоянные нагрузки. Сосредоточенный момент на колонне:

Моменты от нагрузки:

Коэффициенты канонического уравнения:



Угол поворота
=1205,68 / 7,085i = 170,17 / i.
Момент от фактического угла поворота:



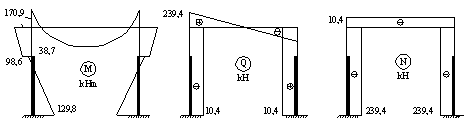
Рис. 8. Эпюры усилий в раме от снеговой нагрузки


Qb = Qa = -(129,8+38,7)/16,2 = -10,4

Nb = Na = -239,4 kH

Nриг = -10,4 kH
Расчет на вертикальную нагрузку от мостовых кранов.

Расчет проводится при расположении тележки крана у левой стойки. Основная система и схема нагрузки приведены на рисунке:


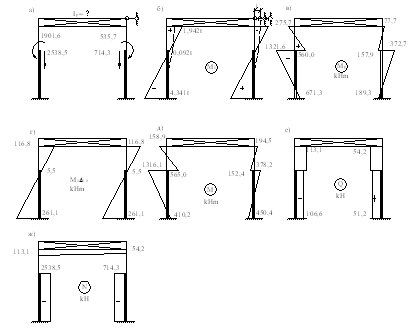
Рис. 9. К расчету рамы на вертикальную нагрузку от кранов.

Проверка возможности считать ригель абсолютно жестким:

Каноническое уравнение для определения смещения плоской рамы:

Моменты и реакции от смещения верхних узлов на ∆=1:

Моменты и реакции на левой стойке от нагрузки:

Усилия на правой стойке можно получить аналогично, или умножая усилия левой стойки на отношение:

---

Реакция верхних концов стоек:

Смещение плоской рамы:

Крановая нагрузка – местная, поэтому . При жесткой кровле по формуле:

– число рам в блоке;

- расстояние между симметрично расположенными относительно середины блока рамами; ( - вторыми от торцов);

- число колес кранов на одной нитке подкрановых балок;

- сумма ординат линии влияния реакции рассматриваемой рамы.

Смещение с учетом пространственной работы:

Эпюра моментов от фактического смещения рамы с учетом пространственной работы см. на (рис. 11, г), а суммарная - на (рис. 11, д).

Эпюра Q (рис. 11, е), свидетельствует о правильном расчете (поперечные силы в верхних и нижних частях стоек рамы практически одинаковы).

Разница в значениях нормальной силы (рис. 11, ж) с левого и правого концов ригеля получилась за счет передачи горизонтальных сил на соседние рамы.

Расчет на горизонтальные воздействия мостовых кранов.

Основная система, эпюра , каноническое уравнение, коэффициент - такие же, как и при расчете на вертикальную нагрузку от мостовых кранов.

Момент и реакция в основной системе от силы Т:

Смещение верхних концов с учетом пространственной работы:

---

Эпюры М и Q показаны на рис. 12.


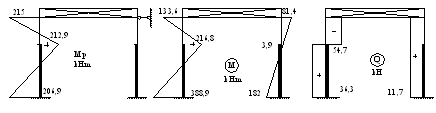
Рис. 12. Эпюры усилий от горизонтальных воздействий мостовых кранов.
Расчет на ветровую нагрузку.

Основная система и эпюра - как для крановых воздействий. Эпюра на правой стойке (рис. 13.):


Коэффициенты канонического уравнения:

Смещение рамы (ветровая нагрузка воздействует на все рамы блока и поэтому ):

Эпюра показана на рис. 13, б.

Эпюра Q (рис. 2.9, в) на левой стойке:

На правой стойке:



Проверка (при правильном решении сумма поперечных сил внизу, должна быть равна сумме всех горизонтальных нагрузок):







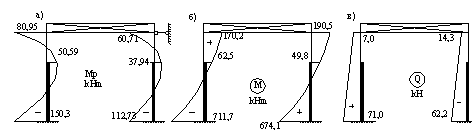
Рис. 13. Эпюры усилий от ветровой нагрузки.
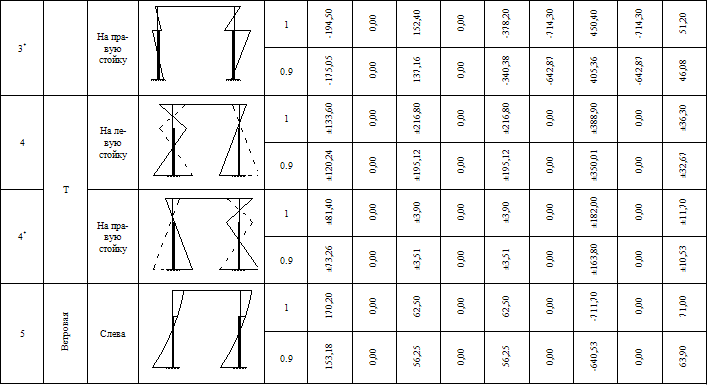
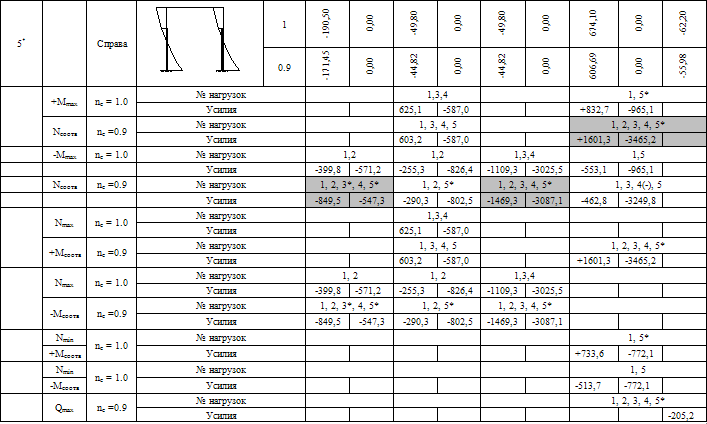
Таблица 2. Таблица расчётных усилий в сечениях левой стойки рамы (изгибающие моменты, кНм, нормальные и поперечные силы, кН)

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Психология социальноправовой деятельности Практическое задание 2.docx

• Подготовила студентка 3 курса фгму32004.pptx

• Аутистического спектраОсобенности психического развития детей с расстройствами аутистического спектра.pdf

• Вопросы и задания к зачету по дисциплине Маркетинг и управление проектами.docx

• Контрольная работа опнн18. 03. 0202. 01. 081 Кр 1 Исполнитель студент гр. Бмоз2221 С. О. Чернихов.docx