ВУЗ: Казахская Национальная Академия Искусств им. Т. Жургенова
Категория: Книга
Дисциплина: Не указана
Добавлен: 03.02.2019
Просмотров: 21688
Скачиваний: 19

11-22 Broadcast Transmission Systems
and the power flow per unit area W = P
t
/4
πr
2
, where P
t
is the total power radiated by the source
and W is represented in W/m
2
. In the engineering of broadcasting and of some other radio ser-
vices, it is conventional to measure the intensity of radiation in terms of the strength of the elec-
tric field E
o
rather than in terms of power density W. The power density is equal to the square of
the field strength divided by the impedance of the medium, so for free space:
(11.2.1)
and:
(11.2.2)
or:
(11.2.3)
Where:
P
t
= watts radiated
E
o
= the free space field in volts per meter
r = the radius in meters
A more conventional and useful form of this equation, which applies also to antennas other
than isotropic radiators, is:
(11.2.4)
where g
t
is the power gain of the antenna in the pertinent direction compared to an isotropic radi-
ator.
An isotropic antenna is useful as a reference for specifying the radiation patterns for more
complex antennas but does not in fact exist. The simplest forms of practical antennas are the
electric doublet and the magnetic doublet, the former a straight conductor that is short compared
with the wavelength and the latter a conducting loop of short radius compared with the wave-
length. For the doublet radiator, the gain is 1.5 and the field strength in the equatorial plane is:
(11.2.5)
2
120
o
E
W
π
=
2
2
4
120
o
t
r E
P
π
π
=
2
2
30
o
t
r E
P
=
30
t
t
o
g P
E
r
=
45
t
o
P
E
r
=
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Propagation

Propagation 11-23
For a half-wave dipole, namely, a straight conductor one-half wave in length, the power gain is
1.64 and:
(11.2.6)
From the foregoing equations it can be seen that for free space:
•
The radiation intensity in watts per square meter is proportional to the radiated power and
inversely proportional to the square of the radius or distance from the radiator.
•
The electric field strength is proportional to the square root of the radiated power and
inversely proportional to the distance from the radiator.
11.2.2a
Transmission Loss Between Antennas in Free Space
The maximum useful power P
r
that can be delivered to a matched receiver is given by [1]:
W
(11.2.7)
Where:
E = received field strength in volts per meter
λ = wavelength in meters, 300/F
F = frequency in MHz
g
r
= receiving antenna power gain over an isotropic radiator
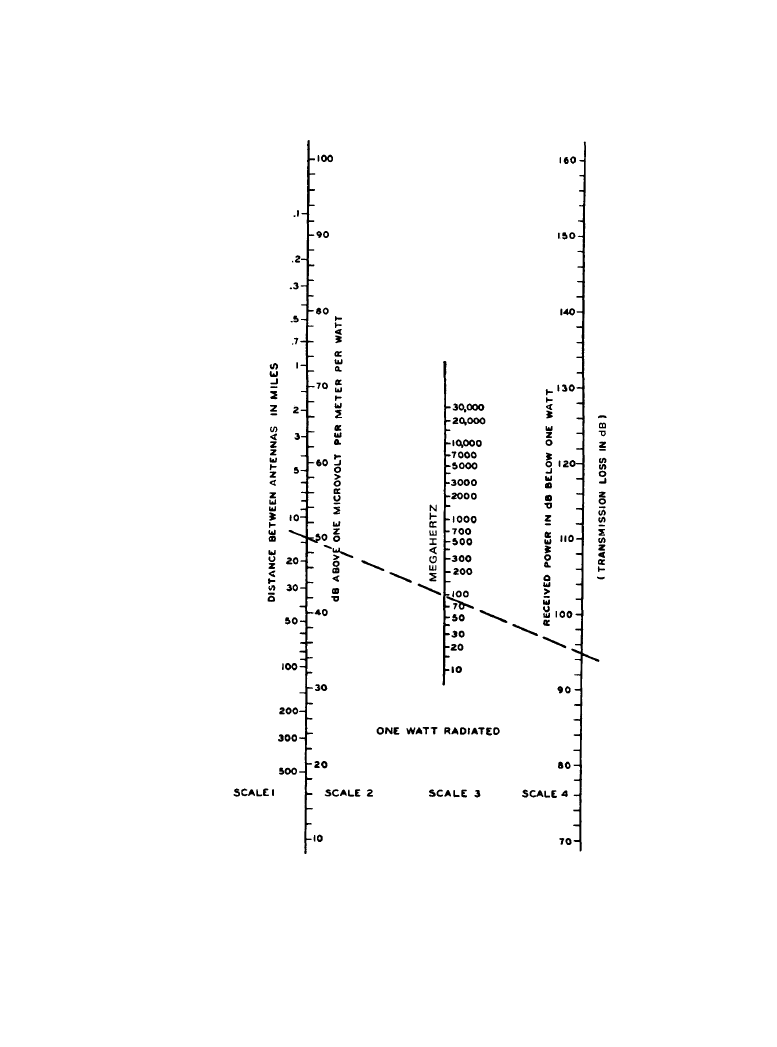
This relationship between received power and the received field strength is shown by scales 2,
3, and 4 in Figure 11.2.1 for a half-wave dipole. For example, the maximum useful power at 100
MHz that can be delivered by a half-wave dipole in a field of 50 dB above 1
µV/m is 95 dB
below 1 W.
A general relation for the ratio of the received power to the radiated power obtained from
Equations (11.2.4) and (11.2.7) is:
(11.2.8)
When both antennas are half-wave dipoles, the power-transfer ratio is:
(11.2.9)
and is shown on scales 1 to 4 of Figure 11.2.2. For free-space transmission, E/E
o
= 1.
7
t
o
P
E
r
=
P
r
E
λ
2
π
-------
2
g
r
120
---------
=
P
r
P
t
-----
λ
4
πr
---------
2
g
t
g
r
E
E
o
------
2
=
P
r
P
t
-----
1.64
λ
4
πr
--------------
2
E
E
o
------
2
0.13
λ
r
--------------
2
E
E
o
------
2
=
=
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Propagation
11-24 Broadcast Transmission Systems
Figure 11.2.1
Free-space field intensity and received power between half-wave dipoles. (
From [2].
Used with permission.)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Propagation

Propagation 11-25
When the antennas are horns, paraboloids, or rnultielement arrays, a more convenient expres-
sion for the ratio of the received power to the radiated power is given by the following:
(11.2.10)
where B
t
and B
r
are the effective areas of the transmitting and receiving antennas, respectively.
This relation is obtained from Equation (11.2.8) by substituting as follows:
(11.2.11)
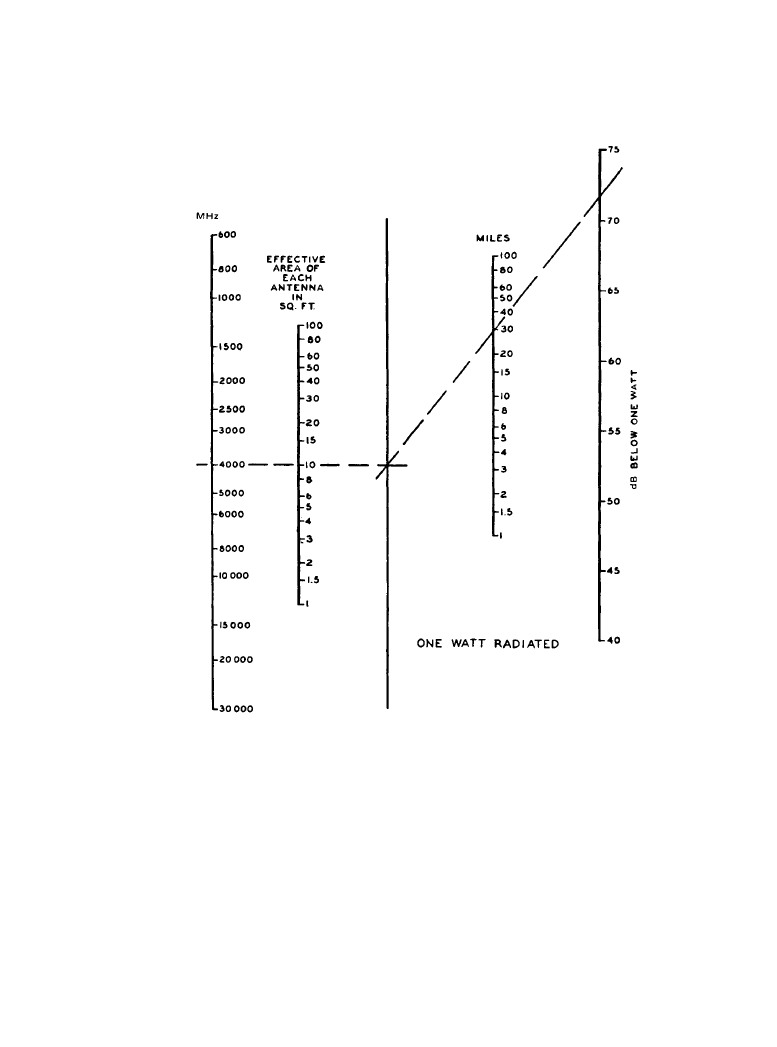
This is shown in Figure 11.2.2 for free-space transmission when B
t
= B
r
. For example, the free-
space loss at 4000 MHz between two antennas of 10 ft
2
(0.93 m
2
) effective area is about 72 dB
for a distance of 30 mi (48 km).
11.2.3 Propagation Over Plane Earth
The presence of the ground modifies the generation and propagation of radio waves so that the
received field strength is ordinarily different than would be expected in free space [3, 4]. The
ground acts as a partial reflector and as a partial absorber, and both of these properties affect the
distribution of energy in the region above the earth.
11.2.3a
Field Strengths Over Plane Earth
The geometry of the simple case of propagation between two antennas each placed several wave-
lengths above a plane earth is shown in Figure 11.2.3. For isotropic antennas, for simple mag-
netic-doublet antennas with vertical polarization, or for simple electric-doublet antennas with
horizontal polarization the resultant received field is [4, 5]:
(11.2.12)
For simple magnetic-doublet antennas with horizontal polarization or electric-doublet anten-
nas with vertical polarization at both the transmitter and receiver, it is necessary to correct for the
cosine radiation and absorption patterns in the plane of propagation. The received field is:
(11.2.13)
Where:
E
o
= the free-space field at distance d in the equatorial plane of the doublet
P
r
P
t
-----
B
t
B
r
λr
( )
2
-------------
E
E
o
------
2
=
2
4
B
g
π
λ
=
(
)
1
2
1
2
cos
cos
j
j
o
o
o
E d
E d R e
E
E
R
e
r
r
θ
θ
∆
∆
=
+
=
+
(
)
3
3
1
2
cos
cos
j
o
E
E
R
e
θ
θ
∆
=
+
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Propagation
11-26 Broadcast Transmission Systems
R = the complex reflection coefficient of the earth
j = the square root of –1
e
j
∆
= cos
∆ + j sin ∆
∆ = the phase difference between the direct wave received over path r
1
and the ground-reflected
wave received over path r
2
, which is due to the difference in path lengths
For distances such that
θ is small and the differences between d and r
1
and r
2
can be
neglected, Equations (11.2.12) and (11.2.13) become:
Figure 11.2.2
Received power in free space between two antennas of equal effective areas.
(
From [2]. Used with permission.)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Propagation