Файл: Audio and Radio Engineering.pdf

5-22 Sound Reproduction Devices and Systems

5.2.2b

Acoustic Characteristics of Rigid Disk with Constant-Force Drive

This section comments on the types of sound-pressure-frequency characteristics produced at a
remote distance on the center axis of a diaphragm and the acoustic output obtained therefrom
when a circular piston diaphragm is placed in an infinite rigid wall and driven at a given force.
When a circular diaphragm with radius 

α is subjected to a constant force F' moving in the axial

direction, sound pressure P is determined by

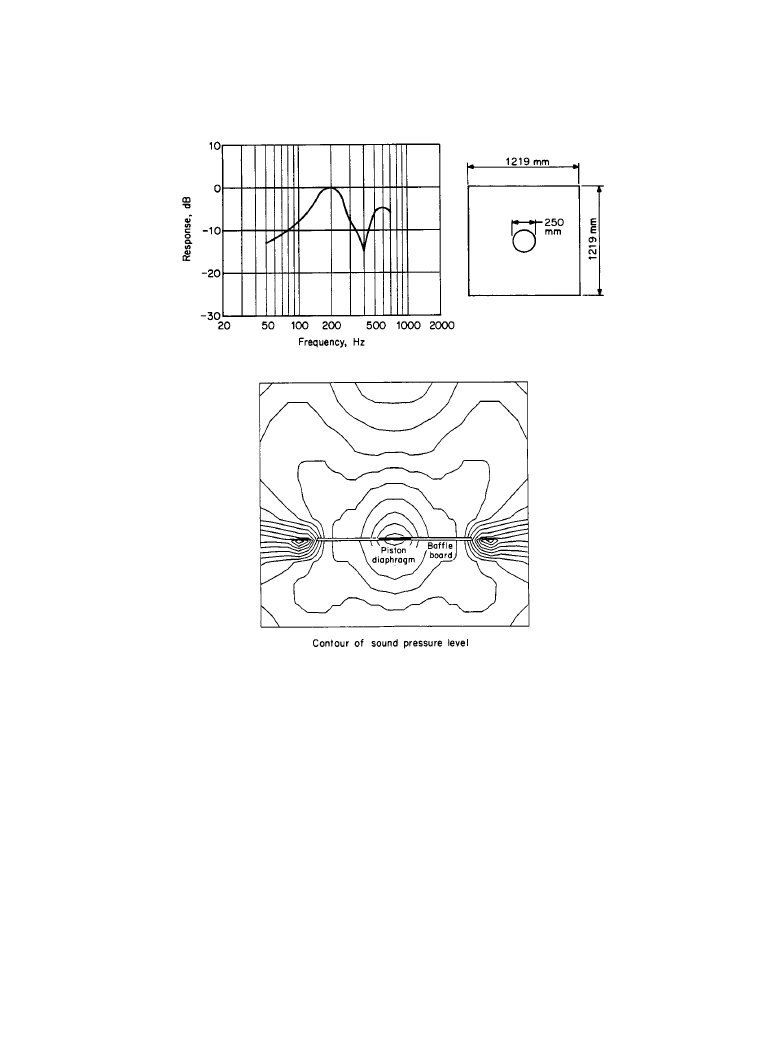
Figure 5.2.5

 Pressure-response-frequency characteristics for a direct radiator installed in the cen-

ter of a finite baffle, estimated by FEM.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Direct-Radiator Loudspeakers

Direct-Radiator Loudspeakers 5-23

(5.2.7)

The absolute value 

 of sound pressure is shown in the equation

P

·

pθ

∂φ

∂t

-----

j

ωp

θ

a

2

2r

---------------exp

jkr

–

(

) v·

⋅

=

=

j

ωp

θ

a

2

2r

---------------exp jkr

–

(

)

F

·

Z

·

---

⋅

=

P

·

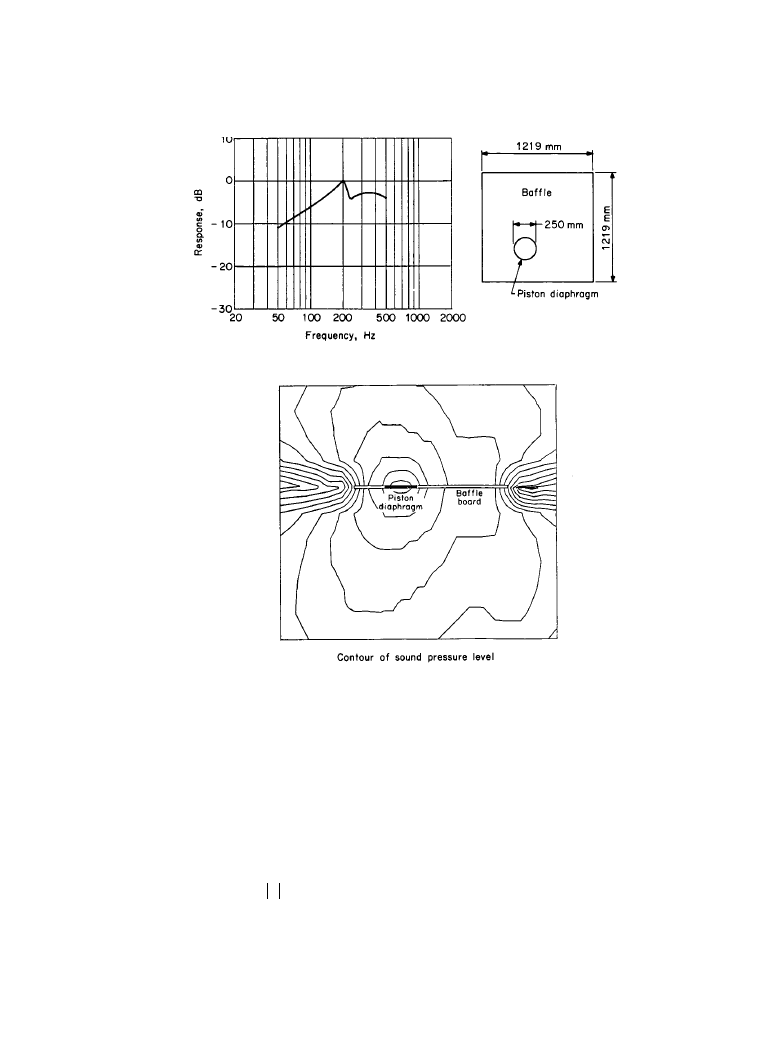
Figure 5.2.6

 Pressure-response-frequency characteristics of a direct radiator installed off center,

estimated by FEM.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Direct-Radiator Loudspeakers

5-24 Sound Reproduction Devices and Systems

(5.2.8)

Where:
P = sound pressure on the axis, N/m

2

p

θ

 = gas density, kg/m

3

θ = velocity potential
a = diaphragm radius, m
r = distance from diaphragm on the axis, m

 = driving force, N

ω = angular frequency, rad/s

When the oscillation system is regarded as a single resonance system,   is obtained as fol-

lows

(5.2.9)

Where:

 = mechanical impedance of oscillation system, mechanical ohms 

r

m

 = mechanical resistance of oscillation system, N/m

C

m

 = oscillation-system compliance, m/N 

m = mass of oscillation system, kg

Therefore, sound pressure 

 is determined by

(5.2.10)

(5.2.11)

T

his is shown in Figure 5.2.7.

(5.2.12)

(5.2.13)

P

·

ωp

θ

a

2

2r

--------------- F

·

Z

·

---

=

P

·

Z

·

Z

·

r

m

j

ωm

1

j

ωC

m

-------------

+

+

=

Z

·

P

·

P

·

ω

2

p

θ

a

2

C

m

2r

------------------------- F·

=

ω ω

θ

<

P

·

p

θ

a

2

2rm

----------- F·      

ω ω

θ

>

=

W

a

πp

θ

a

4

ω

4

C

m

2c

2

----------------------------- F·

2

     ka

1

<

ω ω

θ

<

=

W

a

πpa

4

ω

2

2cr

2

------------------ F·

2

ka

1

<

ω

ω

θ

=

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Direct-Radiator Loudspeakers

Direct-Radiator Loudspeakers 5-25

(5.2.14)

(5.2.15)

(5.2.16)

(5.2.17)

Where:
C = sound velocity, m/s
k = number of waves
ω = resonance angular frequency, rad/s

5.2.3

Bibliography

Beranek, L. L.: Acoustics, McGraw-Hill, New York, N.Y., pg. 185, 1954.

W

a

πpa

4

2cm

2

------------- F·

2

     ka

1

<    ω ω

θ

>

=

W

a

πpa

2

c

ω

2

C

m

2

F

·

2

ka

1

ω ω

θ

>

>

=

W

a

πpa

2

r

2

------------ F·

2

     ka

1   

ω

>

ω

θ

=

=

W

a

πpa

2

c

ω

2

m

--------------- F·

2

     ka

1

ω ω

θ

>

>

=

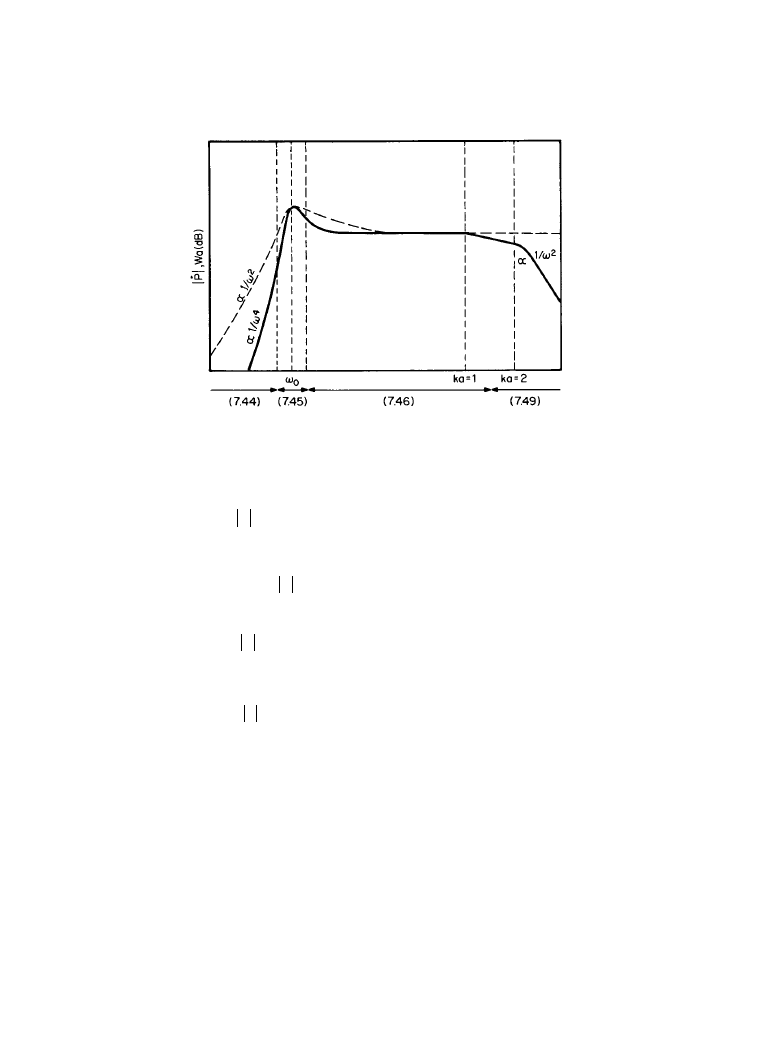
Figure 5.2.7

 Acoustic power and pressure-response-frequency characteristics of a piston source

in an infinite-plane baffle.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Direct-Radiator Loudspeakers

5-26 Sound Reproduction Devices and Systems

Hayasaka, T., and S. Yoshikawa: Onkyo-Kogaku Gairon (An Introduction to Sound and Vibra-

tion), 1983.

Morse, P. M.: Vibration and Sound, McGraw-Hill, New York, N.Y., pg. 326, 1948.

Morse, P. M., and K. U. Ingard: Theoretical Acoustics, McGraw-Hill, New York, N.Y., pg. 366,

1968.

Olson, H. F.: Elements of Acoustical Engineering, Van Nostrand, Princeton, N.J., pg. 38, 1957.

Rayleigh, J. W. S.: The Theory of Sound, Dover, New York, N.Y., pg 162, 1945.

Sakamoto, N.: Loudspeaker and Loudspeaker Systems, Nikkan Kogyo Shinbunshya, pg. 18,

1967.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Direct-Radiator Loudspeakers