ВУЗ: Казахская Национальная Академия Искусств им. Т. Жургенова
Категория: Книга
Дисциплина: Не указана
Добавлен: 03.02.2019
Просмотров: 21690
Скачиваний: 19
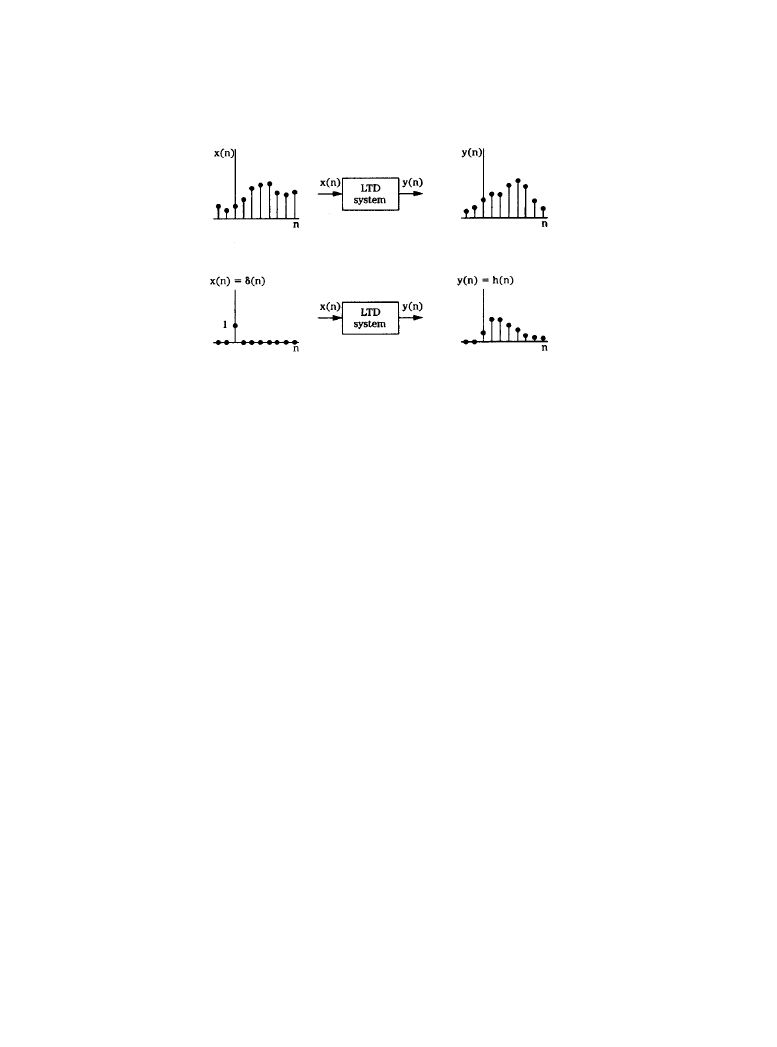
DSP Devices and Systems 6-31
signal, as shown in Figure 6.4.1a. However, an LTD system has a special property such that when
an impulse (a delta function) is applied to an LTD system, the output is the system’s impulse
response, as shown in Figure 6.4.1b. The impulse response describes the system in the time
domain, and can be used to reveal the frequency response of the system in the frequency domain.
Practically speaking, most digital filters are LTD systems, and yield this property. A system is
stable if any input signal of finite amplitude produces an output signal of finite amplitude. In
other words, the sum of the absolute value of every input and the impulse response must yield a
finite number. Useful discrete systems are stable.
Furthermore, the impulse response can be sampled and used to filter a signal. Audio and
video samples themselves are impulses, represented as numbers. The signal could be filtered, for
example, by using the samples as scaling values: all of the values of a filter’s impulse response
are multiplied by each signal value. This yields a series of filter impulse responses scaled to each
signal sample. To obtain the result, each scaled filter impulse response is substituted for its mul-
tiplying signal sample. The filter response can extend over many samples; thus, several scaled
values might overlap. When these are added together, the series of sums forms the new filtered
signal values.
This is the process of convolution. The output of a linear system is the convolution of the
input and the system's impulse response. Convolution is a time-domain process that is equivalent
to the multiplication of the frequency responses of two networks. Convolution in one domain
(such as the time domain) is equivalent to multiplication in the conjugate domain (such as fre-
quency). Furthermore, the duality exists such that multiplication in the time domain is equivalent
to convolution in the frequency domain.
Because convolution is not an intuitive phenomenon, a graphical illustration of its nature is
useful. Consider the waveform in Figure 6.4.2a. It can be divided into discrete pieces such that
x(t) = x
1
(t) + x
2
(t) + x
3
(t) + ..
In other words
(
b)
Figure 6.4.1
Two properties of linear-time-invariant discrete (LTD) systems: (
a) LDT systems pro-
duce an output signal based on the input, (
b) an LTD system can be characterized by its impulse
response. (
van den Enden and Verhoeckx. From [1]. Used with permission.)
(
a)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
DSP Devices and Systems
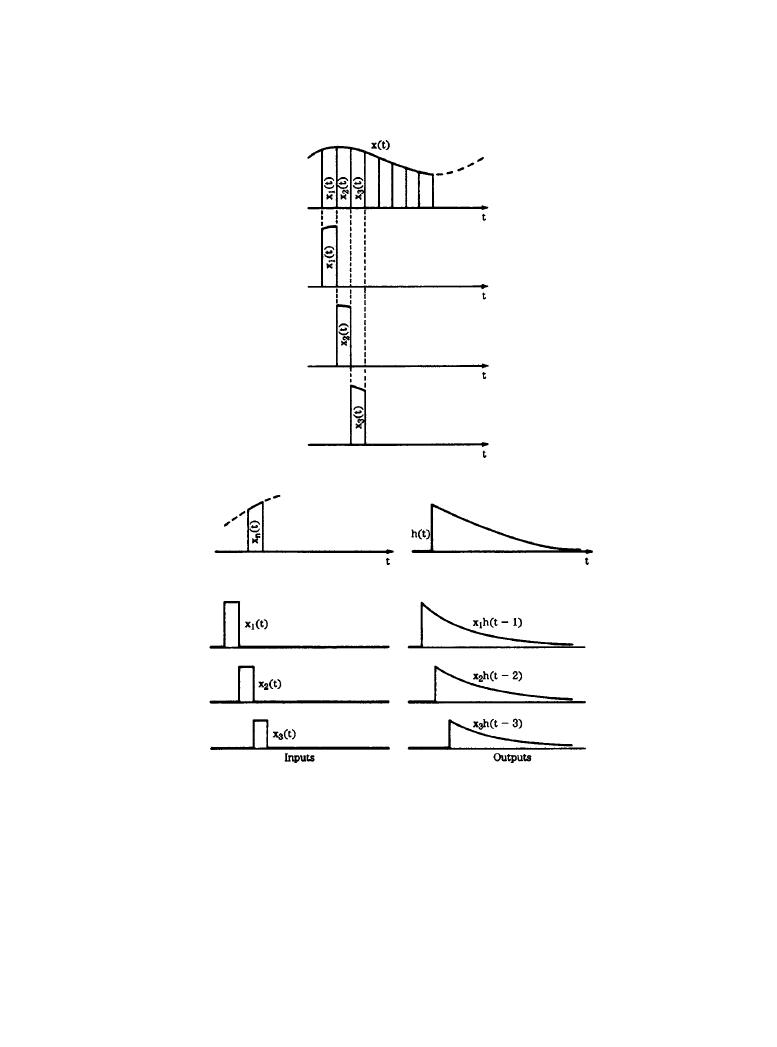
6-32 Digital Coding of Audio Signals
(
a)
(
b)
(
c)
Figure 6.4.2
A graphical representation of convolution: (
a) the samples comprising a discrete sig-
nal may be considered singly, (
b) when applied to a discrete processing system such as a digital
filter, each sample produces an output response, (
c) the overall response is the summation of the
individual responses. (
Blesser. From [1]. Used with permission.)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
DSP Devices and Systems

DSP Devices and Systems 6-33
(6.4.1)
where k = 1, 2, 3,. . .
Consider a network that produces an output h(t) when a single piece of the waveform is input,
as shown in Figure 6.4.2b. The output h(t) defines the network; from this single response we can
find the network’s response to any input. Similarly, the inputs that follow produce outputs that
are scaled and delayed by the delay of the input, as shown in Figure 6.4.3c. The sum of the indi-
vidual responses is the full response to the input waveform:
(6.4.2)
Equivalently,
(6.4.3)
This is convolution, mathematically expressed as:
(6.4.4)
To view convolution in action, consider a series of snapshots of the terms present at five con-
secutive sample times
(6.4.5)
The response is the sum of the terms in each column:
x t
( )
x
k
t
( )
k
x
–
=
x
∑
=
y n
( )
h k
( )x n k
–
(
)
k
1
=
x
∑
=
y n
( )
x k
( )h n k
–
(
)
k
1
=
x
∑
=
y n
( )
h n
( )*x n
( ) where * denotes convolution
=
t = 0T t = 1T t = 2T t = 3T t = 4T
x
0
h
0
x
0
h
1
x
0
h
2
x
0
h
3
x
0
h
4
x
1
h
0
x
1
h
1
x
1
h
2
x
1
h
3
x
2
h
0
x
2
h
1
x
2
h
2
x
3
h
0
x
3
h
1
x
4
h
0
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
DSP Devices and Systems

6-34 Digital Coding of Audio Signals
(6.4.6)
The convolved response is found by reversing the impulse response, and aligning h
0
with the cur-
rent x
k
sample to generate the ordered weighted product. The rest of the sequence is obtained by
moving the reversed impulse response until it has passed through the duration of the samples of
interest, be it finite or infinite in length.
More generally, when two waveforms are multiplied together, their spectra are convolved, and
if two spectra are multiplied, their determining waveforms are multiplied. The response to any
input waveform can be determined from the impulse response of the network, and its response to
any part of the input waveform. As noted, the convolution of two signals in the time domain cor-
responds to multiplication of their Fourier transforms in the frequency domain (as well as the
dual correspondence). It is apparent, then, that any signal can be considered to be a sum of
impulses.
6.4.2c
Complex Numbers
Analog and digital networks share a common mathematical basis [1]. Fundamentally, whether
the discussion is one of resistors, capacitors, and inductors, or scaling, delay, and addition (all
linear, time-invariant elements), processors can be understood through complex numbers. A
complex number z is any number that can be written in the form z = x + jy where x and y are real
numbers, and where x is the real part, and jy is the imaginary part of the complex number. An
imaginary number is any real number multiplied by j, where j is the square root of –1. The form
x + jy is the rectangular form of a complex number, and represents the two-dimensional aspects
of numbers. For example, the real part can denote distance, and the imaginary part can denote
direction. A vector can thus be constructed, showing the indicated location.
A waveform can also be described by a complex number. This is often expressed in polar
form, with two parameters: r and
θ. The form re
j
θ
also can be used. If a dot is placed on a circle
and rotated, perhaps representing a waveform changing over time, the dot’s location can be
expressed by a complex number. A location of 450 would be expressed as 0.707 + 0.707j. A
location of 900 would be 0 + 1j, 135º would be –0.707 + 0.707j, and 180º would be –1 + 0j. The
size of the circle could be used to indicate the magnitude of the number.
The j operator can also be used to convert between imaginary and real numbers. A real num-
ber multiplied by an imaginary number becomes complex, and an imaginary number multiplied
by an imaginary number becomes real. Multiplication by a complex number is analogous to
phase shifting. For example, multiplication by j represents a 90° phase shift, and multiplication
by 0.707 + 0.707j represents a 45° phase shift. In the digital domain, phase shift is performed by
time delay. A digital network comprised of delays can be analyzed by changing each delay to a
phase shift. For example, a delay of 10° corresponds to the complex number 0.984 – 0.174j. If
the input signal is multiplied by this complex number, the output result would be a signal of the
same magnitude, but delayed by 10°.
y
o
= x
0
h
0
y
1
= x
0
h
1
+ x
1
h
0
y
2
= x
0
h
2
+ x
1
h
1
+ x
2
h
0
y
3
= x
0
h
3
+ x
2
h
2
+ x
2
h
1
+ x
3
h
0
y
4
= x
0
h
4
+ x
1
h
3
+ x
2
h
2
+ x
3
h
1
+ x
4
h
0
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
DSP Devices and Systems
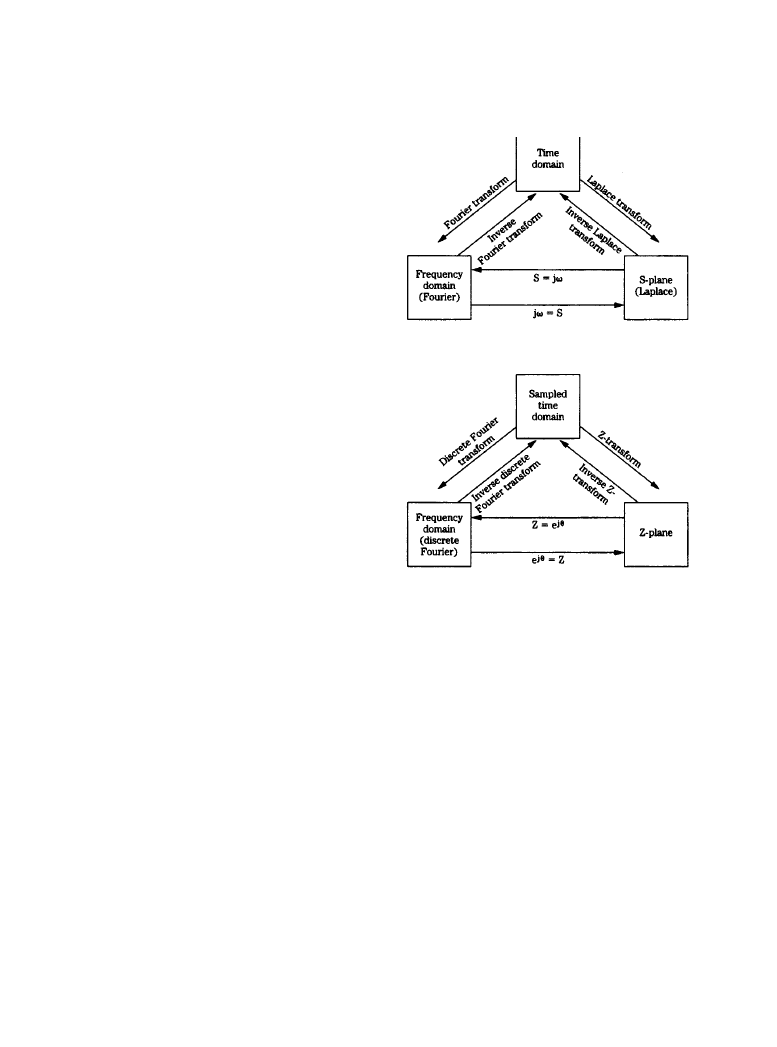
DSP Devices and Systems 6-35
6.4.2d
Mathematical Transforms
Signal processing, either analog or digital, can be considered in either of two domains [1].
Together, they offer two perspectives on a unified theory. For analog signals, the domains are
time and frequency. For sampled signals, they are discrete time and discrete frequency. A trans-
form is a mathematical tool used to move between the time and frequency domains. Continuous
transforms are used with signals continuous in time and frequency; series transforms are applied
to continuous time, discrete frequency signals; and discrete transforms are applied to discrete
time and frequency signals.
The analog relationships between a continuous signal, its Fourier transform, and Laplace
transform are shown in Figure 6.4.3a. The discrete-time relationships between a discrete signal,
its discrete Fourier transform, and z-transform are shown in Figure 6.4.3b.
The Laplace transform is used to analyze continuous time and frequency signals; it maps a
time domain function x(t) into a frequency domain, complex frequency function X(s)
. T
he
Laplace transform takes the form
(6.4.7)
X s
( )
x t
( )e
st
–
t
d
x
–
x
∫
=
Figure 6.4.3
Transforms are used to math-
ematically convert a signal from one
domain to another: (
a) analog signals can
be expressed in the time, frequency, and
s-plane domains, (b) discrete signals can
be expressed in the sampled-time, fre-
quency, and
z-plane domains. (From [1].
Used with permission.)
(
a)
(
b)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
DSP Devices and Systems