Файл: Аппарат дифференциальных уравнений первого порядка.doc

Система (16) называется однородной, если f_i(t)0 (i=1, 2, …, n). Однородная система в векторной форме запишется в виде

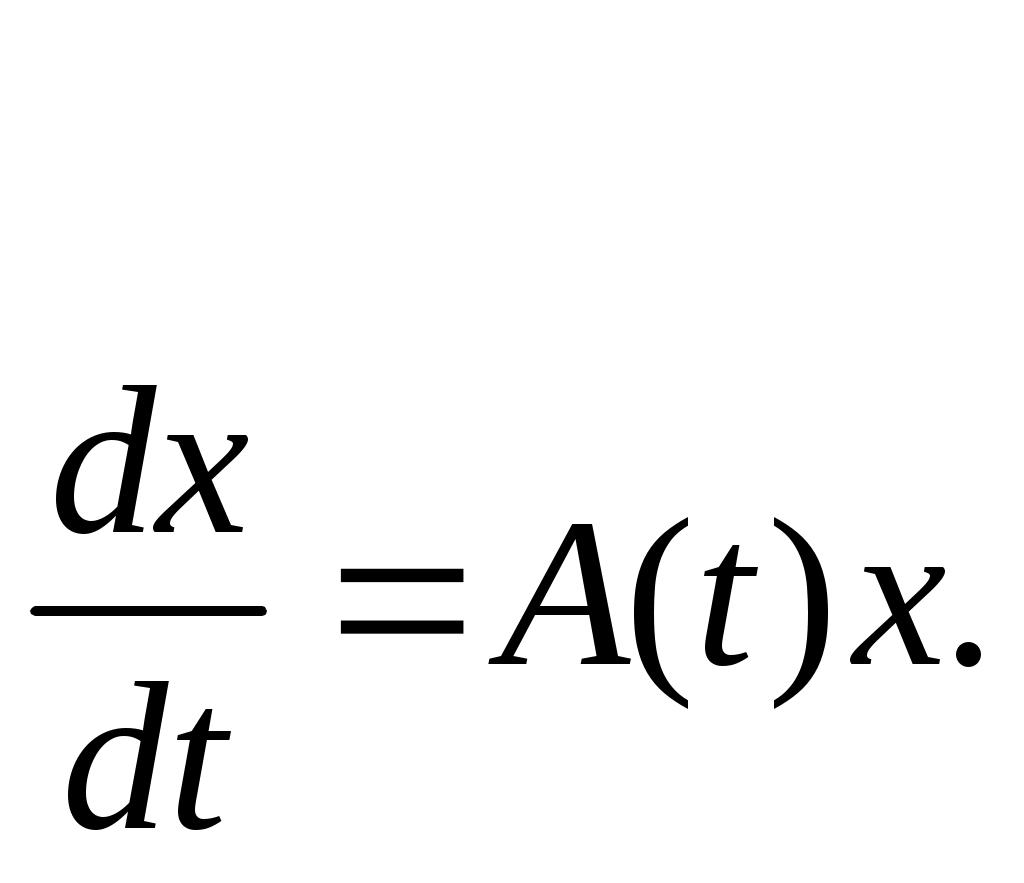⁽¹⁹⁾

Совокупность S всех решений {x(t)} образует линейное пространство размерности n, так как решения этой системы являются линейно-независимыми и образуют базис. Любой элемент этого пространства представим в виде

(20)

причем постоянные c₁, c₂, …, c_n определяются однозначно. Отсюда следует, что любое решение данной системы может быть представлено в виде (20). Поэтому выражение (20) называется общим решением системы (19). Любая система из n линейно-независимых решений системы (19), образующая базис пространства S, называется фундаментальной системой решений.

Физический смысл частного и вспомогательного решений.

Решение однородного уравнения (вспомогательное решение) зависит только от свойств системы и не зависит от входного воздействия. Характеристическое уравнение зависит только от параметров системы, а корни характеристического уравнения определяют вид составляющих вспомогательного решения. В случае отсутствия внешних источников (т. е. система возбуждается запасенной в ней начальной энергией) вспомогательное решение совпадает с общим решением. Таким образом, вспомогательное решение характеризует «естественное» поведение системы при отсутствии внешних возмущений. В связи с этим вспомогательное решение называют также свободным или не вынужденными движением. Если вспомогательное решение системы неограниченно возрастает при стремлении t к бесконечности, говорят, что система неустойчивая. Так как вспомогательное решение содержит экспоненциальные члены, то система станет неустойчивой, если ее характеристическое уравнение содержит корень с положительной действительной частью. С другой стороны, корни с отрицательной действительной частью обусловливают стремление к нулю составляющих решения при стремлении t к бесконечности. При рассмотрении корней характеристического уравнения в комплексной плоскости можно сформулировать следующее утверждение. Если система устойчива, то ее корни должны лежать в левой полуплоскости, а на мнимой оси могут находиться только простые корни.

Если все корни характеристического уравнения лежат в левой полуплоскости

, то вспомогательное решение стремится к нулю при стремлении t к бесконечности и «совпадает» с переходным процессом в системе.

Величины составляющих во вспомогательном решении, т. е. произвольные постоянные решения, зависят от двух факторов, одним из которых является входной сигнал. Другим фактором служит предыстория системы (до момента приложения входного сигнала), которая полностью определяется знанием запасенной в системе энергии к моменту приложения входного воздействия. Вид частного решения обусловливается вынуждающей функцией; его легко усмотреть из метода неопределенных коэффициентов. Время влияет на вид решения лишь в том случае, если составляющая вынужденной функции совпадает с каким-либо членом в у_н. Так как в этом случае система возбуждается на одной из ее собственных частот, то подобное явление называют резонансом.

В связи с тем, что вид частного решения зависит от входного воздействия, его называют также вынужденным движением. Если все корни характеристического уравнения лежат в левой полуплоскости, вынужденное решение совпадает с установившимся движением. Величины вынужденных составляющих зависят как от параметров системы, так и от входного сигнала.

Обычно считают, что вынужденная составляющая решения устанавливается мгновенно при подаче входного сигнала. Свободная же составляющая, т. е. вспомогательное решение, как бы настраивает себя путем правильного определения произвольных постоянных, чтобы обеспечить надлежащий переход системы из невозбужденного состояния в состояние, подчиненное входному воздействию.

Некоторые склонны рассматривать вспомогательное решение как первоначальное сопротивление системы желаниям входа. Величины произвольных постоянных зависят от того, насколько характер входного воздействия отличается от «естественного» поведения системы.

Линейная неоднородная система. Метод вариации произвольных постоянных.

Рассмотрим линейную неоднородную систему (18)

Соответствующая ей однородная система (19)

Пусть x=(t) и (t) – два решения системы (18). Тогда разность

(t)= y(t)–j(t)

Представляет собой решение однородной системы (19).

Общее решение системы (18) имеет вид

где c_i – произвольные постоянные; x_i(t) (i=1, 2, …, n) – фундаментальная система решений системы (19).

Частное решение системы (18) может быть найдено методом вариации произвольных постоянных. Рассмотрим этот метод. Пусть x₁(t), x₂(t), …, x_n(t)— фундаментальная система решений системы (19). Частное решение неоднородной системы (18) будем искать в виде

полагая, что c_i являются не постоянными, а некоторыми функциями t. Подставим это решение в систему (18):

Так как вектор-функции x_i(t) – являются решениями однородной системы (19), то

поэтому

Это выражение представляет собой систему линейных алгебраических уравнений относительно сi(t) (i=l, 2, ,..., n). Определитель этой системы уравнений есть определитель Вронского для фундаментальной системы решений. Он отличен от нуля, поэтому эта система имеет единственное решение с_i’(t)=Ф_i(t) (i=l, 2,..., n).

Интегрируем полученные равенства:

Следовательно, искомое частное решение имеет вид

Значит, общее решение неоднородной системы будет

Дифференциальные уравнения систем автоматического регулирования.

Методика составления дифференциальных уравнений систем автоматического регулирования.

Общие замечания.

Системы автоматического регулирования разнообразны по своему назначению и конструктивному исполнению. Поведение САР может описываться обыкновенными дифференциальными уравнениями в частных производных, разностными уравнениями и т.д.

Любая САР представляет совокупность отдельных взаимодействующих друг с другом элементов, соединенных между собой связями. Первым этапом при составлении дифференциальных уравнений САР является разделение системы на отдельные элементы и составление дифференциальных уравнений этих элементов. Уравнения элементов и уравнения связей между отдельными элементами описывают процесс в системе регулирования, т.е. изменение по времени всех координат системы. Зная уравнения элементов и уравнения связей, можно составить структурную схему САР.

Структурная схема САР характеризует геометрию системы, т.е. показывает, из каких элементов состоит САР и как эти элементы связаны между собой. Состояние САР, а также каждого входящего в нее элемента характеризуется некоторым числом независимых переменных. Этими переменными могут быть как электрические величины (ток, напряжение, и т.д.), так и механические (скорость, угол поворота, перемещение и т.д.). Обычно, чтобы характеризовать состояние системы или ее элемента, выбирают одну обобщенную координату на входе системы или элемента (g(t)) и одну – на выходе (x(t)). В ряде случаев такое представление невозможно, так как система или ее элемент могут иметь несколько входных и выходных величин. В многомерных системах можно рассматривать векторные входную и выходную величины с размерностями, совпадающими соответственно с числом входных и выходных величин САР.

Составление и линеаризация дифференциальных уравнений элементов систем.

При составлении дифференциальных уравнений САР основной задачей является составление дифференциальных уравнений отдельных элементов системы. Уравнение отдельных элементов составляются на основе тех физических законов, которые характеризуют поведение элемента.

При составлении дифференциальных уравнений элементов САР следует стремиться возможно точнее описать поведение данного элемента. Однако сложность получаемых при этом уравнений затрудняет исследование свойств их решений. Поэтому при составлении дифференциальных уравнений необходимо стремиться к разумному компромиссу между возможно более полным описанием поведения элемента и возможностью обозрения и исследования полученных уравнений.

Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение не линейно, то элемент называется нелинейным.

Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решение которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией.

Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента

x=φ(g) некоторой линейной функцией x=ag+b. Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x=φ(g) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов содержащих отклонение ∆g входной величины элемента в степени выше первой. Геометрически это означает замену кривой x=φ(g) касательной, проведенной к кривой в точке (x₀, g₀), соответствующей установившемуся состоянию работы элемента (рис. 29). В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x=φ(g) в требуемом диапазоне изменения входной величины элемента.

Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными.

Рассмотрим процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением

F(xⁿ, x^’, x, g) = 0 (1).

Тогда установившееся состояние элемента характеризуется уравнением F(0, 0, x, g) = 0 (2). пусть g₀ и х₀ – значения установившегося состояния. Тогда координаты g и х можно записать в виде x = x₀ + ∆x, g = g₀ + ∆g, где ∆g и ∆x – отклонение координат g и х от установившегося состояния. Уравнение (1) в отклонениях имеет вид:

F(∆x^’’, ∆x^’, x₀+ ∆x, g₀ + ∆g) = 0 (3).

Разложим левую часть уравнения (3) в ряд Тейлора относительно точки установившегося состояния (0, 0, x₀, g₀):

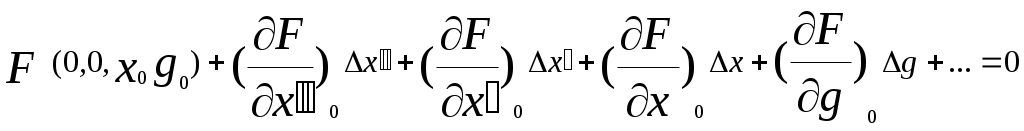(4).

Частные производные в левой части уравнения (4) представляют собой некоторые числа, величины которых зависят от вида функции F(x^’’, x^’, x, g) и значений координат x₀ и g₀.

Считая отклонения ∆g, ∆x от установившегося состояния, а также их производные по времени малыми и пологая, что функция F(x^’’, x^’, x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (4) все члены, которые содержат отклонения ∆g и ∆x, а также их производные в степени выше первой. Полученное уравнение