Добавлен: 10.11.2023
Просмотров: 72
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Понятие дифференциального уравнения
Представление непрерывных систем в виде дифференциальных уравнений.
Преобразование системы дифференциальных уравнений.
Основные свойства линейных дифференциальных уравнений.
Решение дифференциальных уравнений первого порядка
Общее решение линейной однородной системы
Линейная неоднородная система. Метод вариации произвольных постоянных.
Дифференциальные уравнения систем автоматического регулирования.
Методика составления дифференциальных уравнений систем автоматического регулирования.
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»
Дисциплина: Высшая математика
Реферат
Тема: Аппарат дифференциальных уравнений первого порядка
Выполнил(а):
Тарасов А.В
Омск 2023
Содержание:
Понятие дифференциального уравнения 2
Представление непрерывных систем в виде дифференциальных уравнений. 3
Преобразование системы дифференциальных уравнений. 4
Основные свойства линейных дифференциальных уравнений. 7
Решение дифференциальных уравнений первого порядка 8
Общее решение линейной однородной системы 9
Физический смысл частного и вспомогательного решений. 9
Линейная неоднородная система. Метод вариации произвольных постоянных. 11
Дифференциальные уравнения систем автоматического регулирования. 12
Методика составления дифференциальных уравнений систем автоматического регулирования. 12
Общие замечания. 13
Составление и линеаризация дифференциальных уравнений элементов систем. 13
Понятие пространства состояний 16
Понятие управляемости и наблюдаемости. 17
Соотношения вход – состояние – выход 20
Уравнения состояния. 22
Классическим методом описания линейной системы считается записанная при помощи дифференциального или разностного уравнения связь между ее входом и выходом. Дифференциальное уравнение применяется для описания непрерывных систем, а уравнение в конечных разностях — для дискретных систем.
Понятие дифференциального уравнения
Уравнения, которые, кроме неизвестных функций одного или нескольких переменных, содержат также их производные, называются дифференциальными. Дифференциальные уравнения называются обыкновенными, если неизвестные функции являются функциями одного переменного, в противном случае дифференциальные уравнения называются уравнениями в частных производных.
Соотношение вида
называется дифференциальным уравнением n-го порядка. Решением дифференциального уравнения называется функция x=x(t), определенная на некотором интервале t, которая, будучи подставлена в это уравнение, обращает его в тождество на всем интервале . Это уравнение можно рассматривать как функцию, определяющую неявно производную n-го порядка x
(n). При определенных условиях его можно решить относительно x(n):
Пусть x=x(t) – решение данного дифференциального уравнения. Тогда x(t) является непрерывной и непрерывно дифференцируемой функцией t. На плоскости (t,x) решению x=x(t) будет соответствовать непрерывная кривая, называемая интегральной кривой.
Функция x=x(t,C) называется общим решением дифференциального уравнения, если путем соответствующего выбора постоянной можно любую интегральную кривую.
Представление непрерывных систем в виде дифференциальных уравнений.
Непрерывную систему часто описывают дифференциальным уравнением относительно ее выхода y(t) и входа r(t). В общем виде уравнение представляется так:
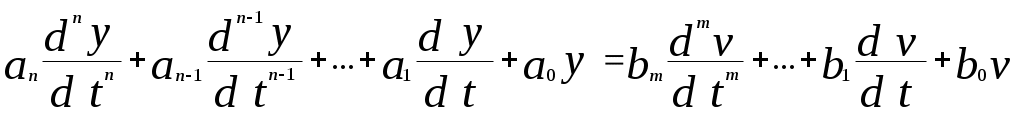 (1)
(1)Предполагая, что входной сигнал v (t) известен, правую часть уравнения можно представить как F(t), называемую часто вынуждающей функцией,
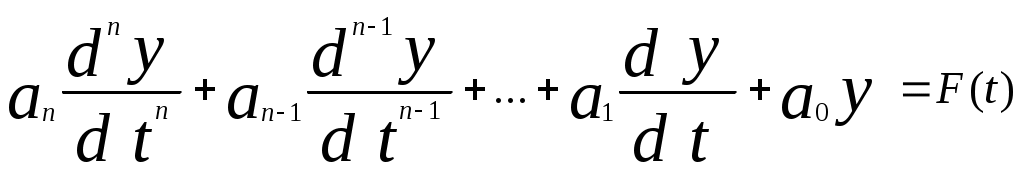 (2)
(2)Для линейных систем аi и bi не являются функциями v или у но могут зависеть от времени t.
Для линейных систем с постоянными параметрами эти коэффициенты должны быть постоянными.
Дифференциальное уравнение системы может быть задано или должно быть найдено на основе модели системы, в последнем случае модель дает непосредственно систему дифференциальных уравнений.
Оператор р, обозначающий часто операцию дифференцирования, определяется как
Если c1 и c2 - постоянные величины, то
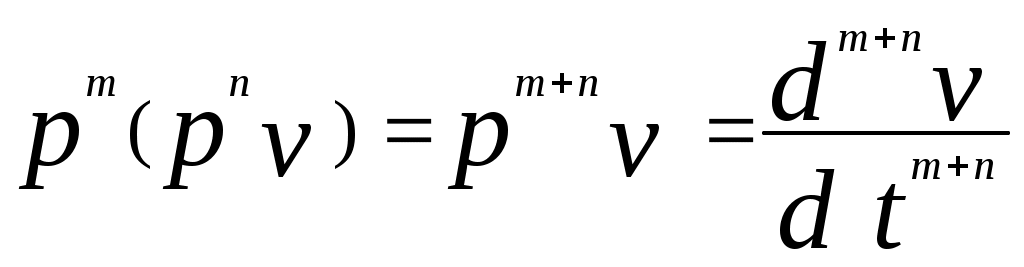 (4),
(4),где n и m неотрицательные целые числа. Как правило, с оператором р можно оперировать как с алгебраическим числом. Существенным исключением является то, что он в общем случае некоммутативен с функциями
p(tv)≠t(pv)
p(v1v2)≠v1(pv2).
При помощи оператора р уравнения (1) и (2) приводятся к виду
(anpn + an-1pn-1 +…+ a1p + a0)y(t) = bmpm +…+ b1p + b0)v(t) = F(t) (7)
стоящие в скобках перед у и v элементы сами являются операторами.
Для стационарных систем, коэффициенты которых постоянны, последнее выражение записывается символически как
A(p)y(t) = B(p)v(t) = F(t).
Для линейных систем с переменными параметрами, коэффициенты которых являются функциями времени, А и В - зависящие от времени
операторы. Это учитывается выражением
A(p, t)y(t) = B(p, t)v(t) = F(t).
Формальное определение операторов А и В следует из сравнения
последних трех выражений.
Преобразование системы дифференциальных уравнений.
Непрерывная модель может быть описана математически системой дифференциальных уравнений. Один класс уравнений служит главным образом для характеристики отдельных составляющих, а другой - для описания связей между этими составляющими. При математическом описании модели указанные два типа уравнений обычно сочетаются с экспериментальной проверкой. Полученная система уравнений может быть затем сведена к одному уравнению, связывающему вход и выход системы, хотя подобное преобразование не всегда элементарно. Решение системы уравнений с постоянными коэффициентами гораздо проще чем системы уравнений с переменными коэффициентами, а потому рассматривается в первую очередь.
Пример: Дли цепи изображенной на рисунке запишем уравнение, связывающее напряжение на выходе е2 с напряжением источника e1. Суммируя токи, выходящие соответственно из узлов 3 и 2, получим
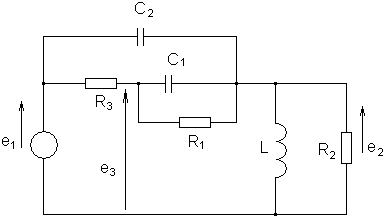
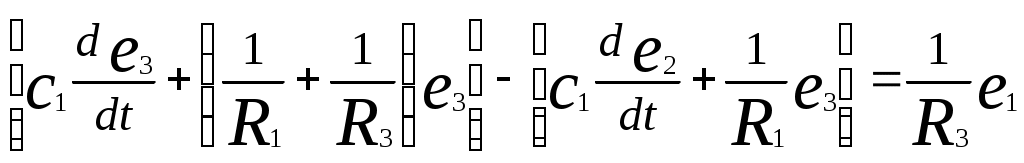
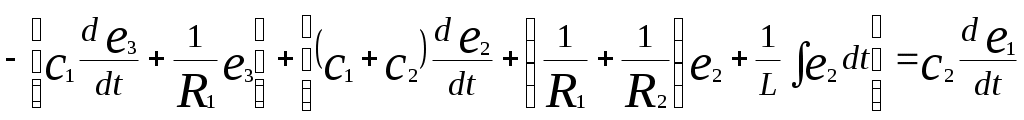 .
.Дифференцируя второе уравнение, чтобы избавиться от интеграла, и вводя оператор р - d/dt, приводим уравнения к виду
(p+2)e3 – (p+1)e2 = e1,
-(p2+p)e3 + (2p2+2p+1)e2 = p2e1.
Предполагается, для простоты, что все сопротивления, емкости и индуктивности равны соответственно 1 ом, 1 фарада, 1 генри. Помножим каждый из членов первого уравнения на оператор р2+р, а каждый из членов второго уравнения - на р + 2 и сложим затем эти уравнения. Поскольку
(p2+p)(p+2)e3 = (p+2)(p2+p)e3,
то выражение, содержащее е3 уничтожится. Тогда
(p+2)(2p2+2p+1)e2 – (p2+p)(p+1)e2 = [(p2+p) + p2(p+2)]e1
или
(p3 + 4p2
+ 4p + 2)e2=(p3 + 3p2 + p)e1, что и является искомым результатом.
Процедура, используемая в данном примере, справедлива для любых двух дифференциальных уравнений с постоянными коэффициентами. Если L означает оператор, являющийся функцией только р, то уравнения можно символически записать как
L11(p)y1(t) + L12(p)y2(t) = F1(t),
L21(p)y1(t) + L22(p)y2(t) = F2(t). (8)
Умножим первое уравнение на L21, а второе на L11 и вычтем одно из другого. Так как L21L11y1=L11L21y1, то
(L11 L22 – L21 L12)y2 = L21F1 + L11F2 (9)
Аналогично,
(L11 L22 – L21 L12)y1 = L22F1 + L12F2 (10)
Каждое из последних двух уравнений содержит лишь одну независимую переменную.
Изложенный материал ограничивался дифференциальными уравнениями с постоянными коэффициентами. Получение дифференциального уравнения, связывающего вход и выход, для систем с переменными коэффициентами гораздо сложнее. Предположим, что система описывается уравнениями
t(py1) + p(t2y2) = F1(t),
p(ty1) + t(py2) = F2(t).
Чтобы исключить у1, из этих уравнений, можно попытаться умножить первое из них на pt, а второе на tp и затем вычесть одно из другого. Если это выполнено, то
pt2(py1) + pt(pt2y2) = ptF1(t),
tp(pty1) + tp(tpy2) = tpF2(t).
Однако pt2(py1) = (t2p2 + 2tp)y1, а tp(pty1) = t(tp2 + 2p) y1. Следовательно, исключить у1 вычитанием нельзя.
Для систем с переменными параметрами уравнения (9) и (10) несправедливы, так как
Основные свойства линейных дифференциальных уравнений.
Линейное дифференциальное уравнение n-го порядка можно записать в форме:
(anpn + an-1pn-1 +…+ a1p + a0)y(t) = F(t). (11)
В связи с тем, что все выражения справедливы как для систем с постоянными, так и с переменными параметрами, коэффициенты аi могут быть в общем случае функциями времени t. Если правая часть последнего уравнение равна тождественно нулю, т. е.
(anpn + an-1pn-1 +…+ a1p + a0)y(t) = 0. (12)
то такое уравнение называют однородным. Уравнение (11) называют соответственно неоднородным дифференциальным уравнением.
Уравнение (12) может иметь не более, чем п линейно независимых решений, n объектов называются линейно зависимыми, если по крайней мере один из них можно выразить в виде линейной комбинации остальных. В противном случае объекты считаются независимыми. Необходимое и достаточное условие линейной независимости n решений уравнения (11) состоит в отличии от нуля определителя Вронского. Если у
1, у2,... уn - n решений уравнения, то определитель Вронского имеет вид
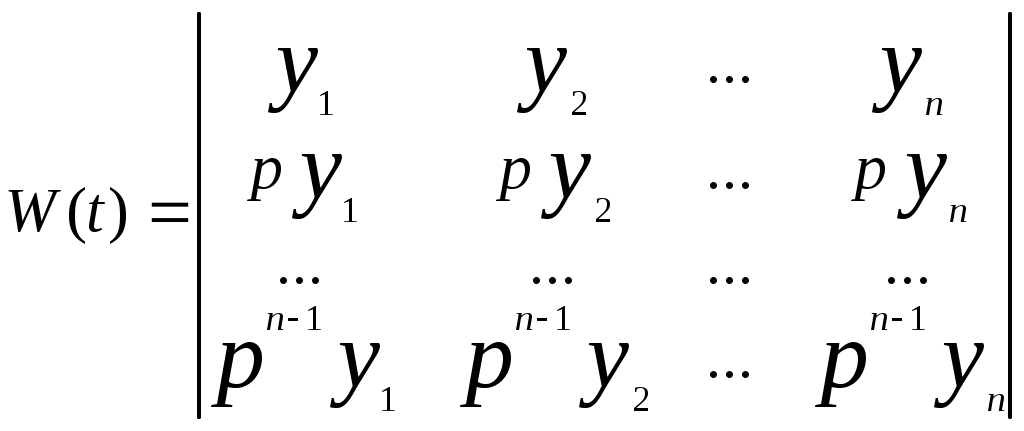 (13)
(13)Общее решение уравнения (11) представляется как
yн = K1y1 + K2y2 +…+ Knyn, (14)
где Ki - произвольные постоянные. Индекс Н указывает на то, что решение соответствует однородному уравнению.
Из последнего уравнения следует, что если известны n независимых решений, то произвольное решение этого уравнения можно представить в виде линейной комбинация n известных решений. Для систем с постоянными параметрами существует общий метод нахождения независимых решений однородного уравнения. Для систем с переменными параметрами такого метода, к сожалению, не существует.
Общее решение неоднородного уравнения (11) имеет вид У=Ун+Уp(15), где ун - решение (14) соответствующего однородного уравнения, ур - произвольное решение (вне зависимости оттого, каким образом оно получено), удовлетворяющее уравнению (11) и обычно называемое частным решением неоднородного уравнения, ун называют вспомогательным решением. Для нахождения ур приемлем любой способ, даже «метод проб». Так как ур не содержит произвольных постоянные то в решении у, как и в ун, содержится n постоянных.
Решение дифференциальных уравнений первого порядка
Линейной системой дифференциальных уравнений называется такая система уравнений, в которую неизвестные функции и их производные могут входить только в первой степени.
Нормальная линейная система дифференциальных уравнений имеет вид
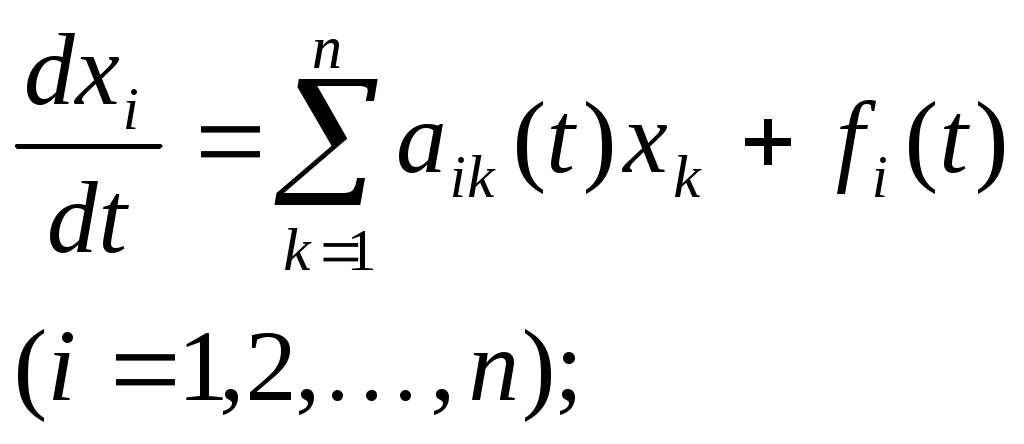 (16)
(16)Введем в рассмотрение векторные функции
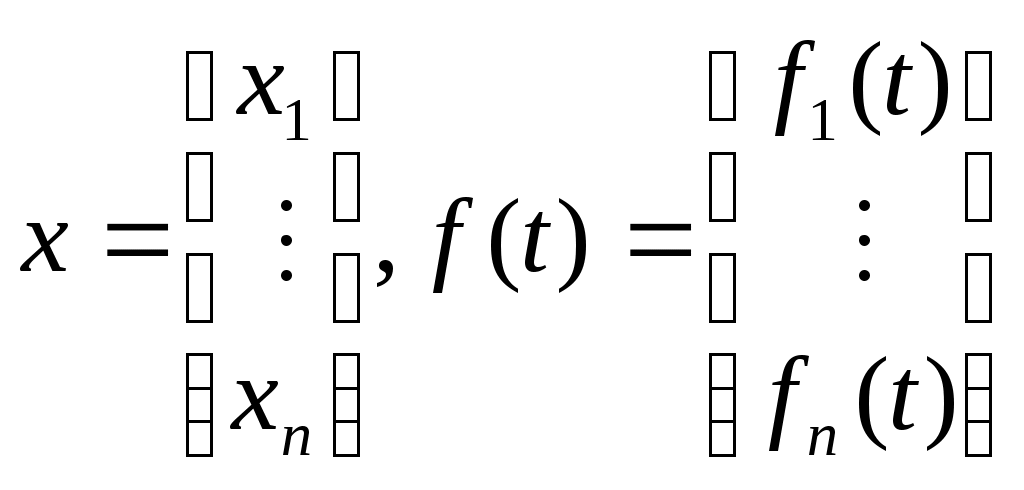 и матрицу
и матрицу 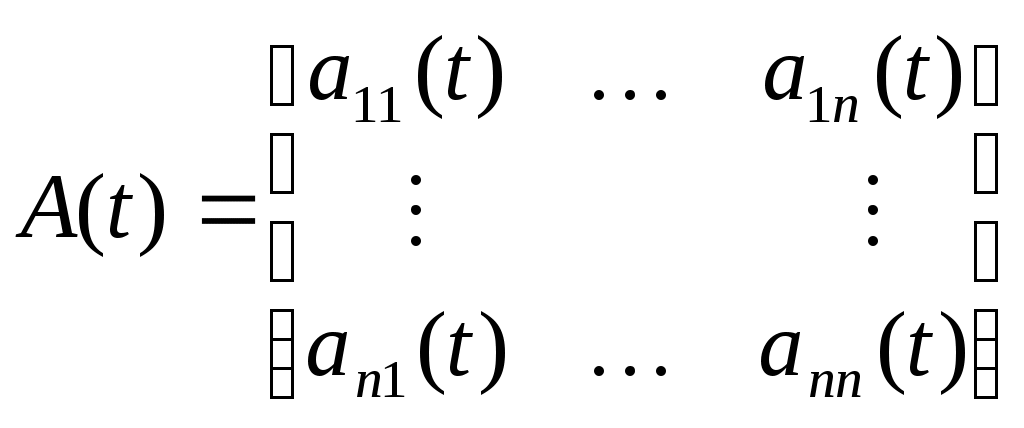 (17)
(17)Тогда систему (1) можно переписать в виде
Теорема существования и единственности справедлива для линейной системы на любом отрезке [а1 ,b1](а, b), где (a, b) - интервал, на котором функции aik(t) и fi(t) непрерывны.