Добавлен: 10.11.2023
Просмотров: 75
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Понятие дифференциального уравнения
Представление непрерывных систем в виде дифференциальных уравнений.
Преобразование системы дифференциальных уравнений.
Основные свойства линейных дифференциальных уравнений.
Решение дифференциальных уравнений первого порядка
Общее решение линейной однородной системы
Линейная неоднородная система. Метод вариации произвольных постоянных.
Дифференциальные уравнения систем автоматического регулирования.
Методика составления дифференциальных уравнений систем автоматического регулирования.
(5) является линейным дифференциальным уравнением с постоянными коэффициентами 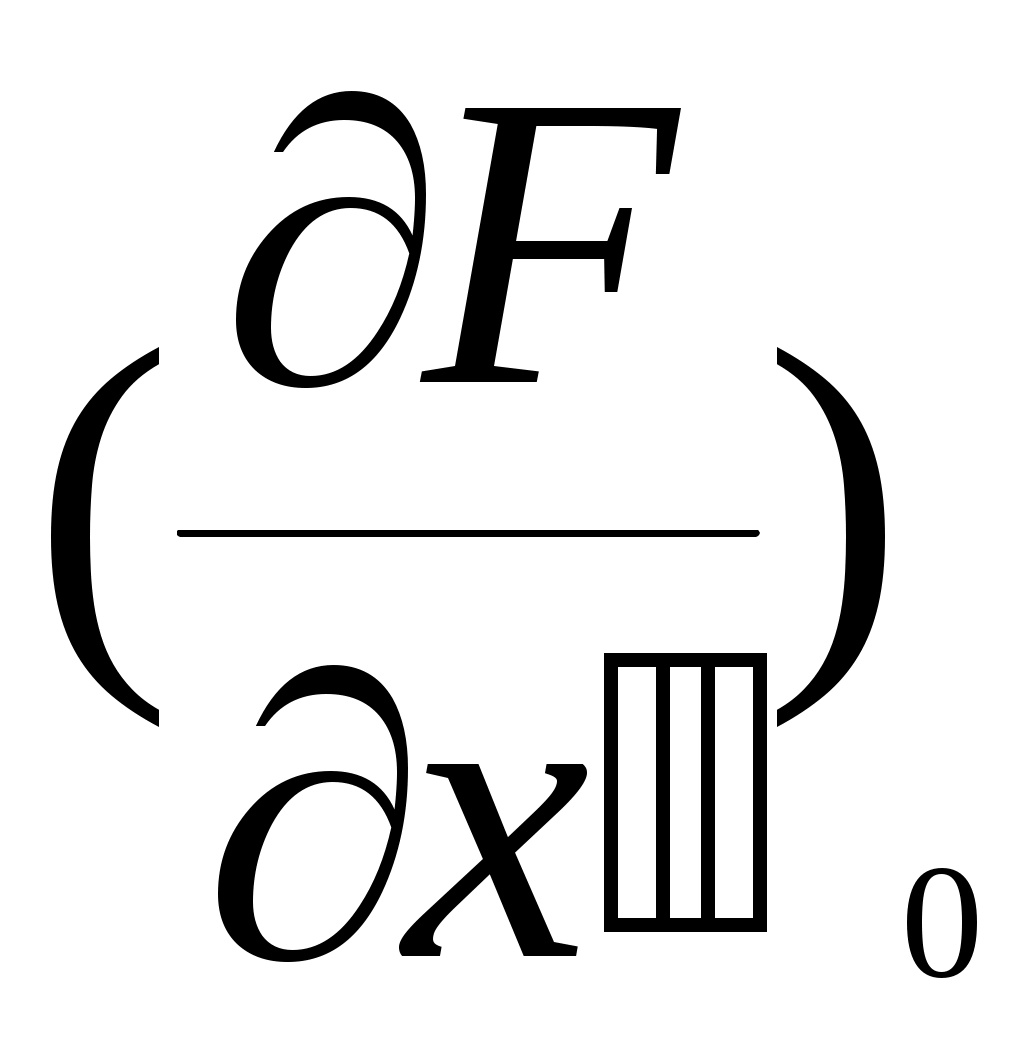 ,
, 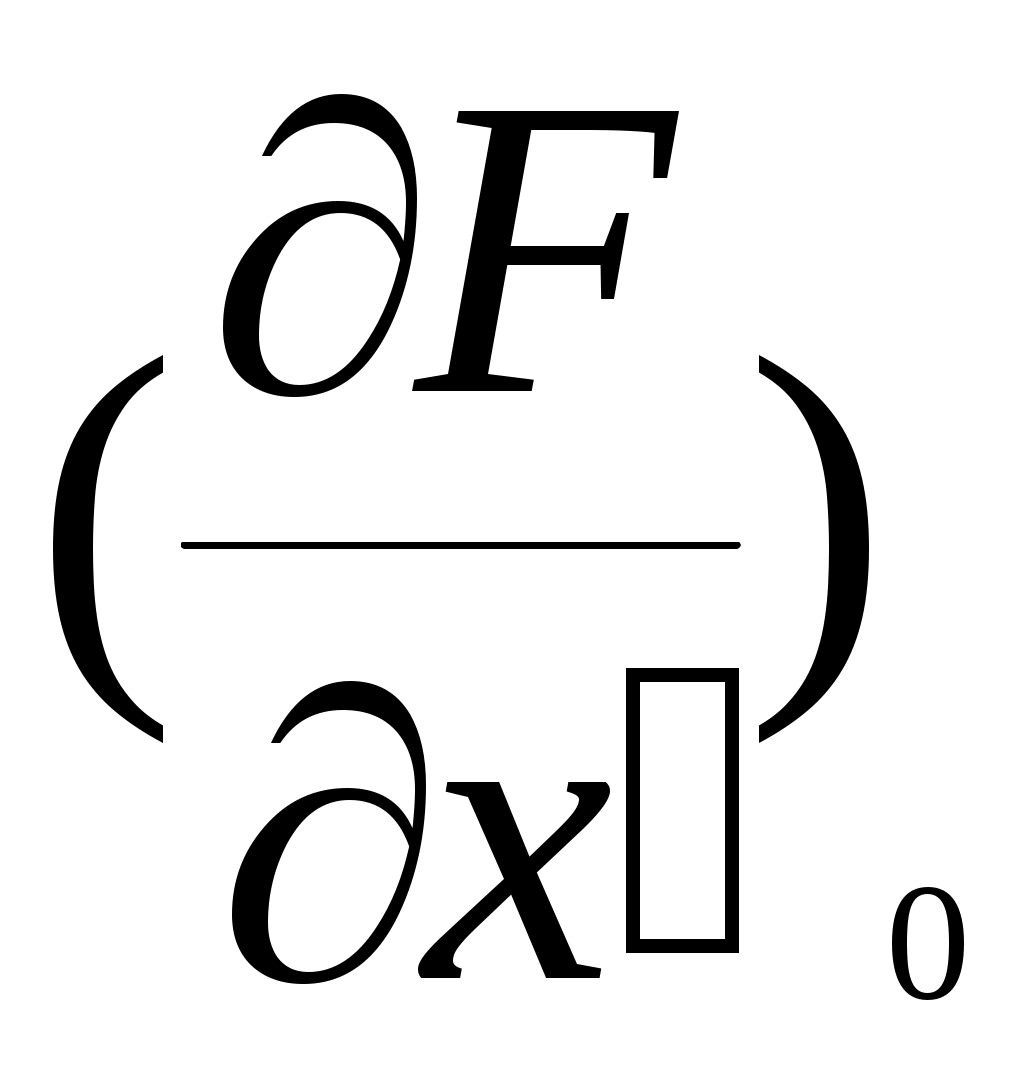 ,
, 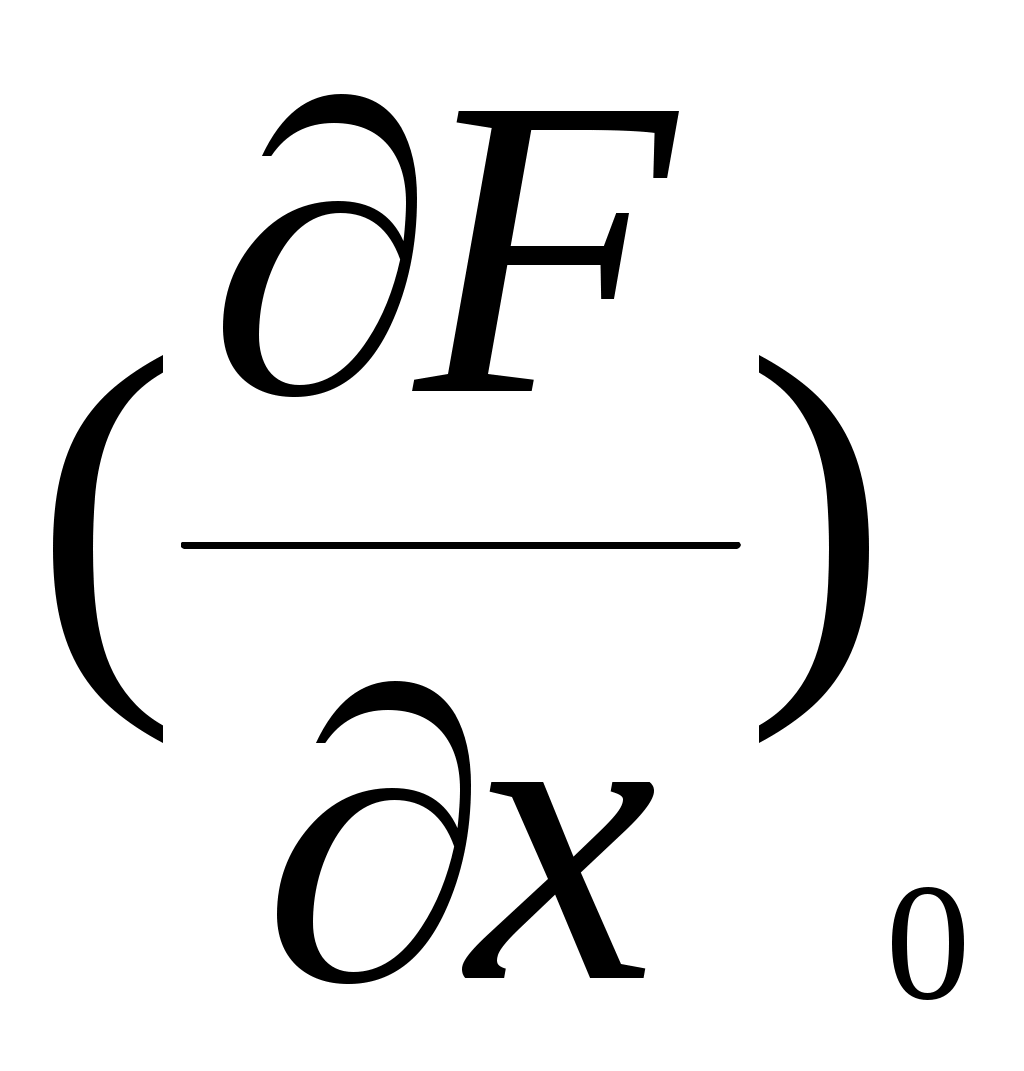 ,
, 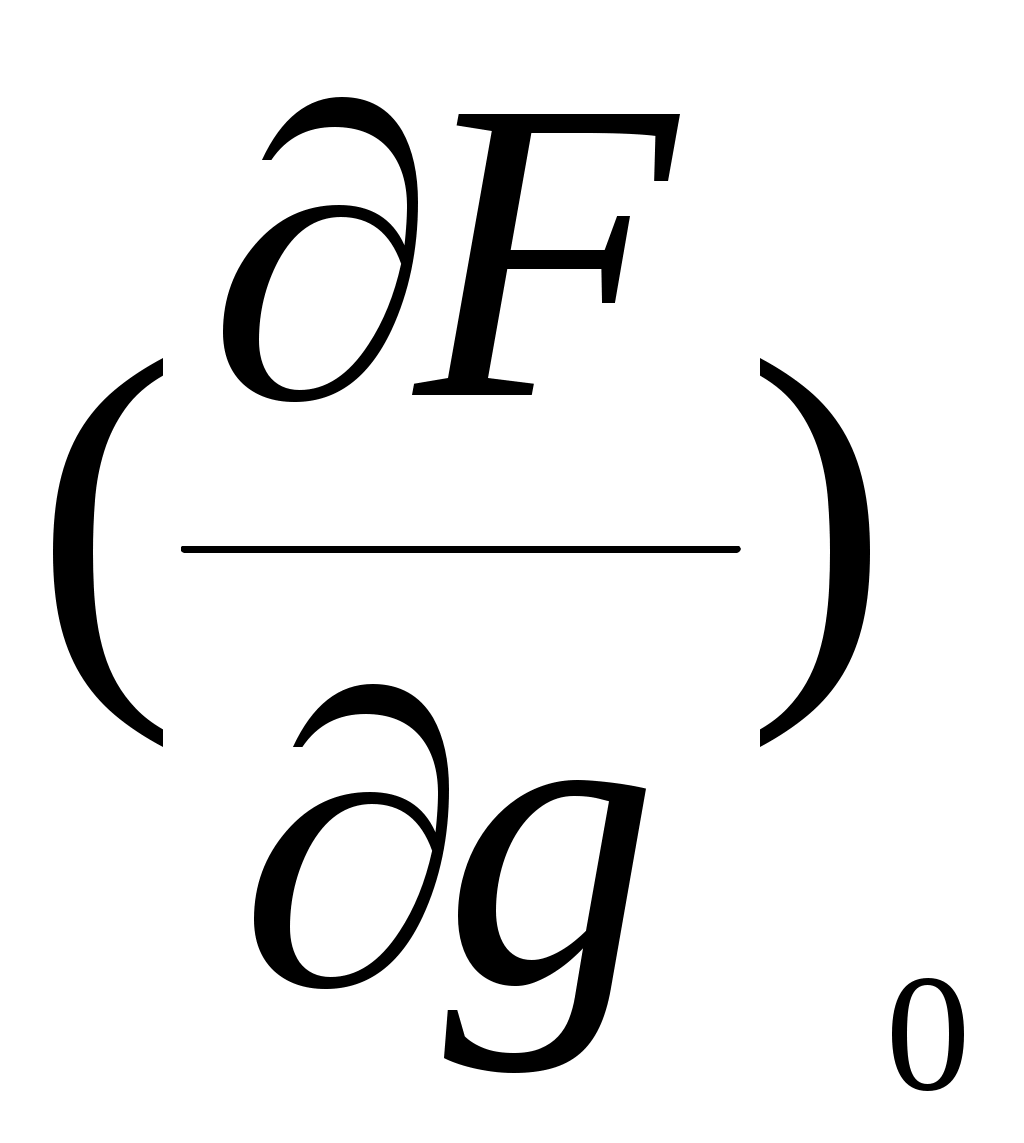 и представляет собой результат линеаризации уравнения (1).
и представляет собой результат линеаризации уравнения (1).
Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x’’, x’, x, g) в окрестности точки, соответствующей установившемуся состоянию.
Процесс линеаризации уравнения (1) может быть геометрически интерпретирован следующим образом. В пространстве переменных x’’, x’, x, g уравнение (1) задает некоторую поверхность. Переход от уравнения (1) к линейному уравнению (5) означает замену поверхности некоторой касательной плоскостью, проведенной к поверхности в точке, соответствующей установившемуся состоянию. Естественно, что ошибка при такой замене тем меньше, чем меньше отличаются друг от друга точки поверхности и точки плоскости. Это справедливо лишь в некоторой малой окрестности установившегося состояния.
С точки зрения анализа и синтеза систем представляется целесообразным разделить все переменные, характеризующие систему, на три группы:
1) входные переменные или входные воздействия mi, представляющие сигналы, генерируемые системами, внешними по отношению к исследуемой, и влияющие на поведение системы;
2) выходные переменные или переменные, характеризующие реакцию системы yj, позволяющие описать некоторые аспекты поведения системы, представляющие интерес для исследователя;
3) переменные (координаты) состояния или промежуточные переменные xk, характеризующие динамическое поведение исследуемой системы.
Величины mi, yj и xk предполагаются функциями времени. Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа, совокупность выходных переменных – в виде вектора выхода, и совокупность переменных состояния – в виде вектора состояния:
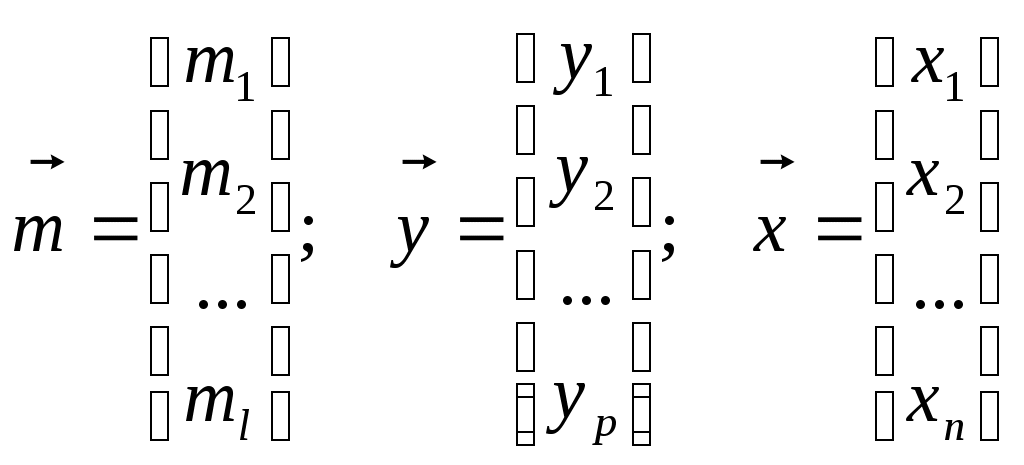 .
.
Множество всех значений, которые может принять вектор входа m в момент t, образует пространство входа системы. Множество всех значений, которые может принять вектор выхода y в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы.
Управляемость: Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением
dx(t)/dt=Ax(t)+Dm(t), (1)
где x – n-мерный вектор состояния; m – r-мерный вектор, представляющий управляющие воздействия; A – квадратная матрица коэффициентов n-го порядка; D – матрица управления размера nxr.
Матрица A может быть приведена к диагональной матрице (или в общем случае к жордановой форме)
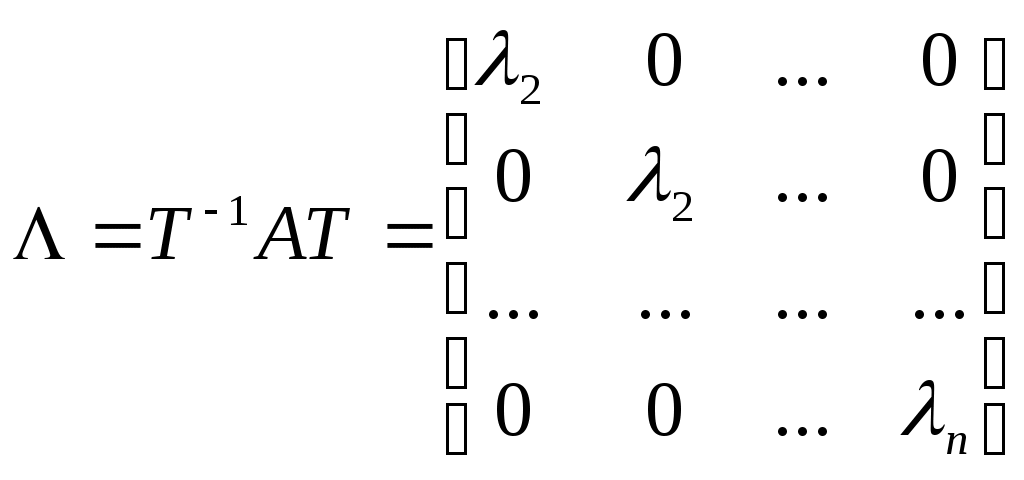
где ш – собственные значения матрицы A, которые предполагаются все различными.
Применяя подстановку x=Tz, исходное уравнение запишется в канонической форме
dz(t)/dt=z(t)+m(t),
где D=T-1D=[ij]nxr.
Вектор z в полученной формуле будем называть каноническим вектором состояния. Будем считать, что в предыдущих матричных выражениях собственные значения li расположены в порядке возрастания их модулей, комплексные li – в порядке возрастания их аргументов, векторы-столбцы матрицы T – нормализованы, то есть выбраны так, что евклидова длина их равна единице.
Запишем полученное выражение в развернутой форме, то есть в виде системы дифференциальных уравнений первого порядка:
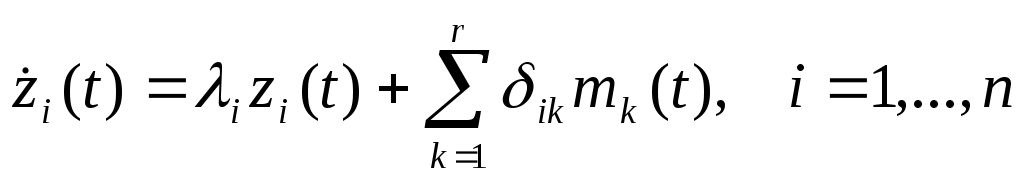
Эти уравнения показывают, что управляющее воздействие mk не будет оказывать какого-нибудь влияния на движение по координате zj, если
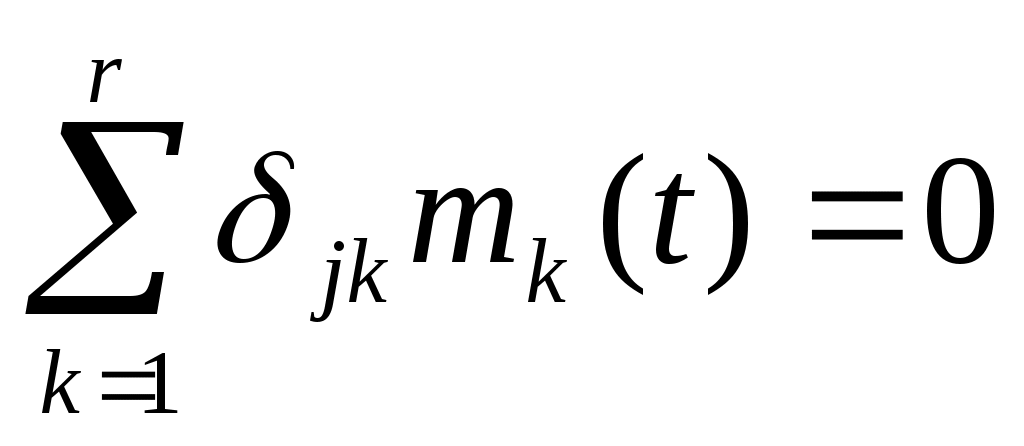
то есть когда jk=0 для k=1, 2, …, r. Запись в такой форме означает, что все элементы j-й строки матрицы D все равны нулю. Отсюда следует вывод, что неуправляемыми координатами системы являются все те канонические координаты, которые соответствуют нулевым строкам матрицы D. Равенство нулю всех элементов этих строк матрицы D делает невозможным управление по соответствующим координатам. Это означает также, что изменение координат происходит независимо от управляющих воздействий и, следовательно, целиком определяется начальными условиями и возмущениями. Можно сказать, что эти координаты развязаны от управления.
Приведенное рассмотрение позволяет дать следующее определение управляемости: процесс, описываемый уравнением (1), является полностью управляемым, если матрица
D не содержит строк, элементы которых равны нулю; координаты, соответствующие ненулевым строкам D, считаются управляемыми.
Наблюдаемость: Перепишем еще раз выражение для вектора выхода линейного многомерного процесса:
y(t)=Bx(t)+Gm(t), (1)
где y – p-мерный вектор, представляющий выходные переменные; B – матрица выхода размером pxn; G – матрица обхода системы размера pxr.
Пусть матрица B имеет вид
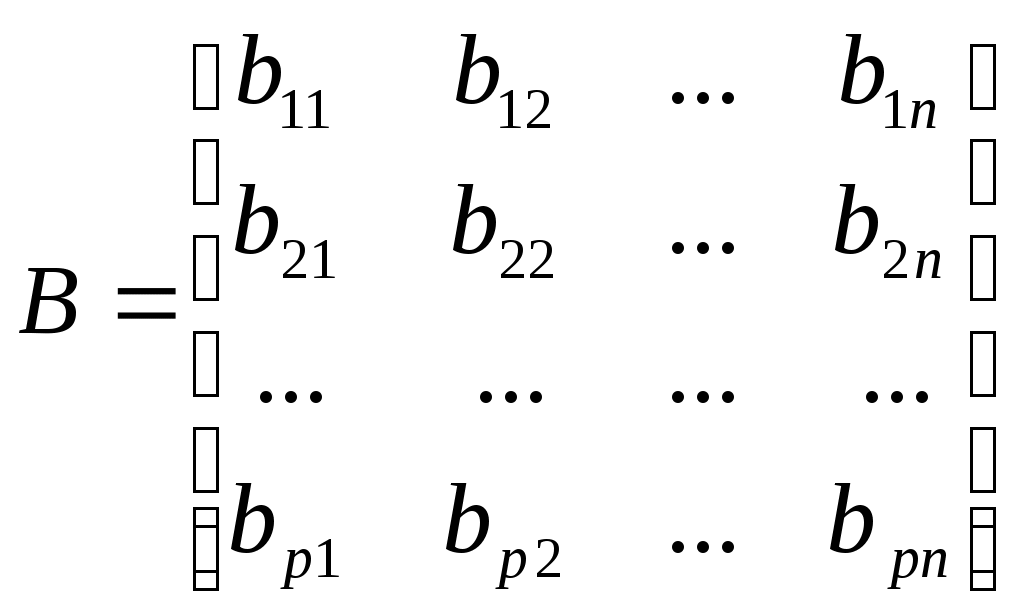
а матрица обхода G задана в виде
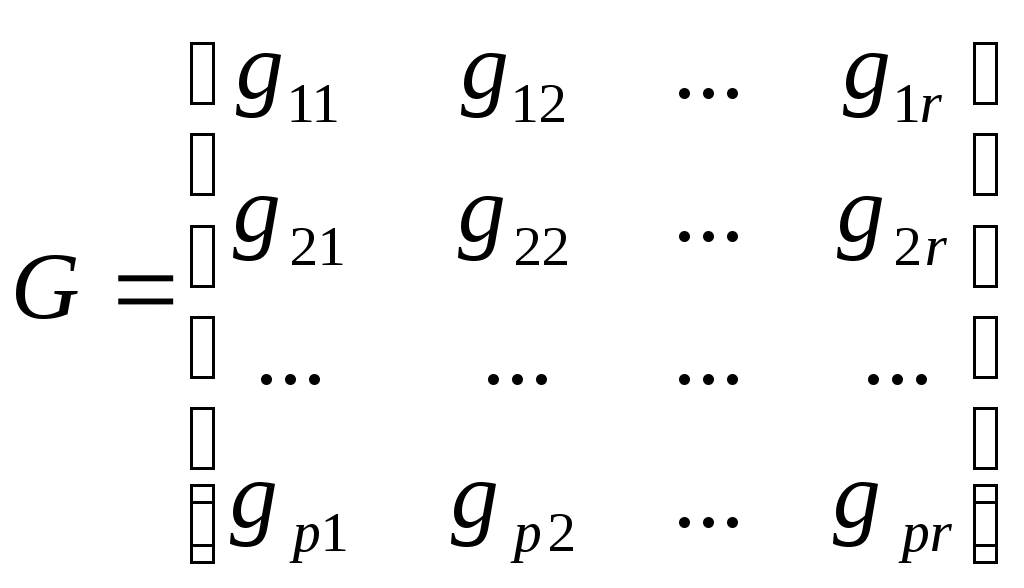
Тогда, развертывая формулу (1), получаем p выражений
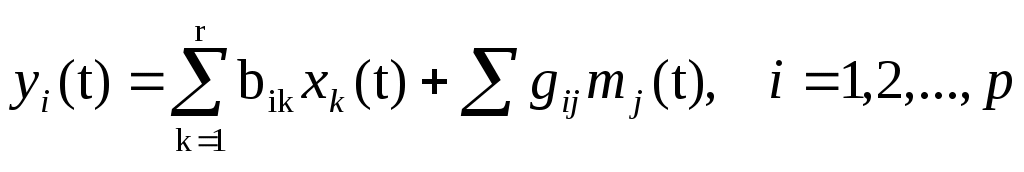 (2)
(2)
Координату состояния принято называть наблюдаемой, если она может быть определена или для нее может быть получена оценка по измеримым выходным переменным. Анализ уравнений (2) показывает, что координата xk может быть определена или для нее может быть получена оценка по измеримым выходным переменным y1, y2, …, yi, …, yp, если коэффициенты bik для i=1, 2, …, p не все равны нулю. Другими словами, xk является наблюдаемой координатой, если элементы k-го столбца матрицы выхода не все равны нулю. Если это условие не соблюдается, то координату xk называют ненаблюдаемой. Таким образом, линейный процесс является наблюдаемым, если матрица выхода B не содержит столбцов, элементы которых равны нулю.
Пусть R – система, описываемая соотношением вход-выход вида
L(p)y = u1 (1),
где L(p) = anpn +…+ a0, an≠0 и ai,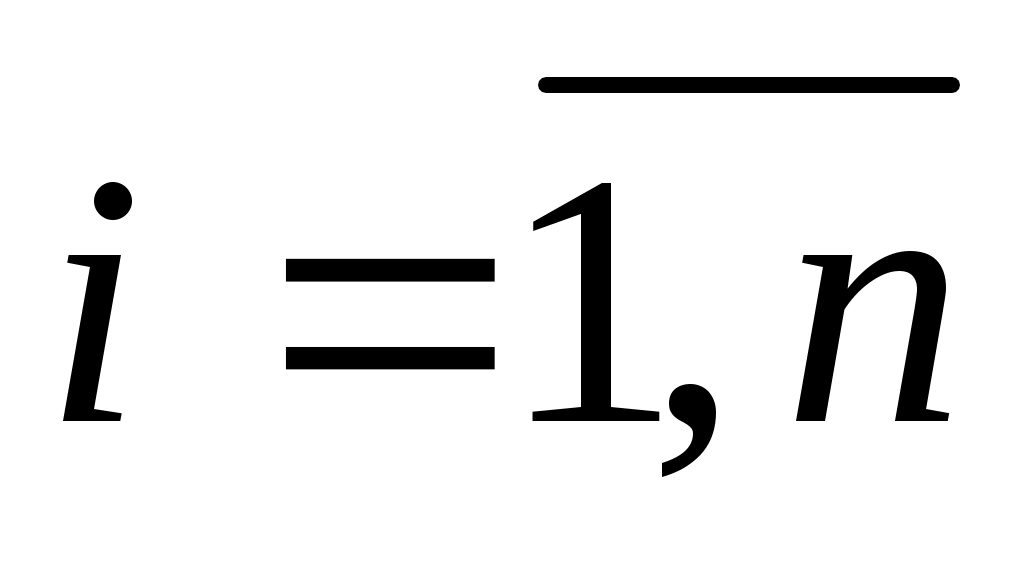 - постоянные, не обязательно вещественные. Тогда выражение для общего решения (1) будет
- постоянные, не обязательно вещественные. Тогда выражение для общего решения (1) будет
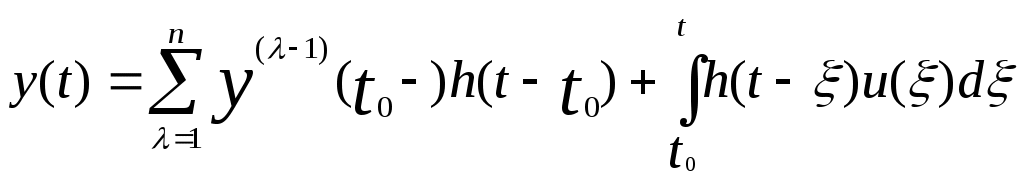 , t ≥ t0 (2)
, t ≥ t0 (2)
где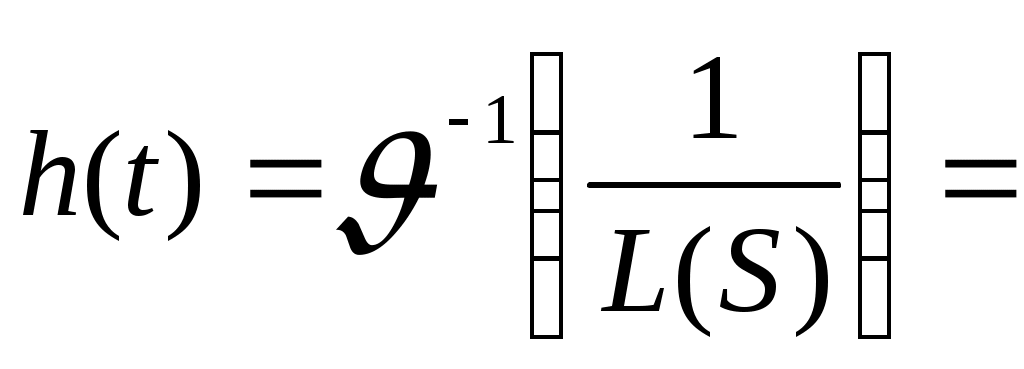 импульсной реакции
импульсной реакции  ,
,
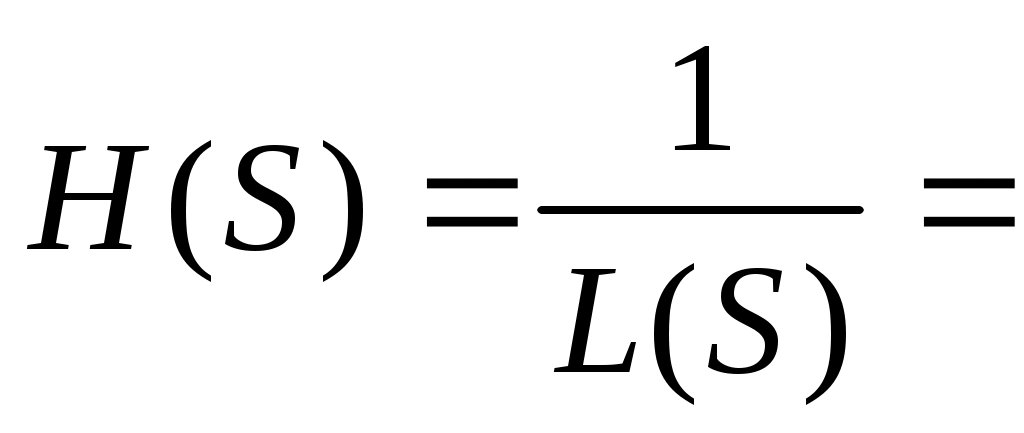 передаточной функции
передаточной функции  , (3)
, (3)
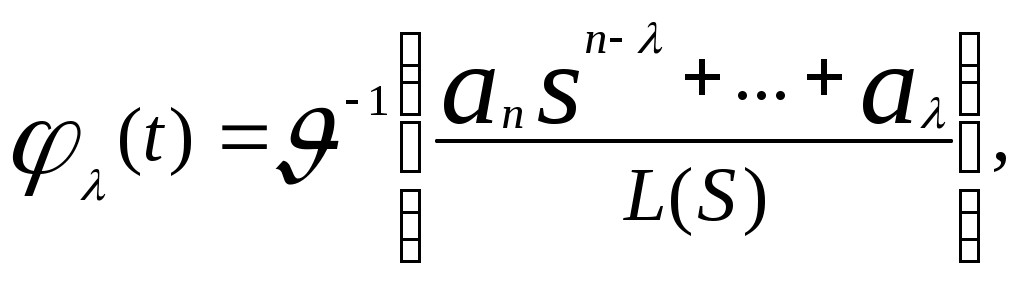
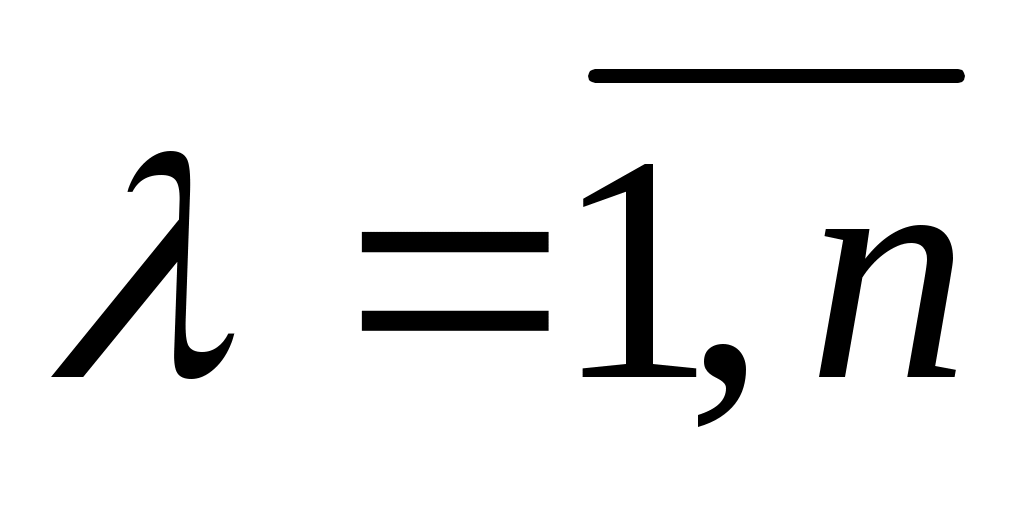 .
.
Функции времени φ1,…, φn линейно независимые и удовлетворяют условию (дифференциальному уравнению)
L(p) φλ(t) = 0,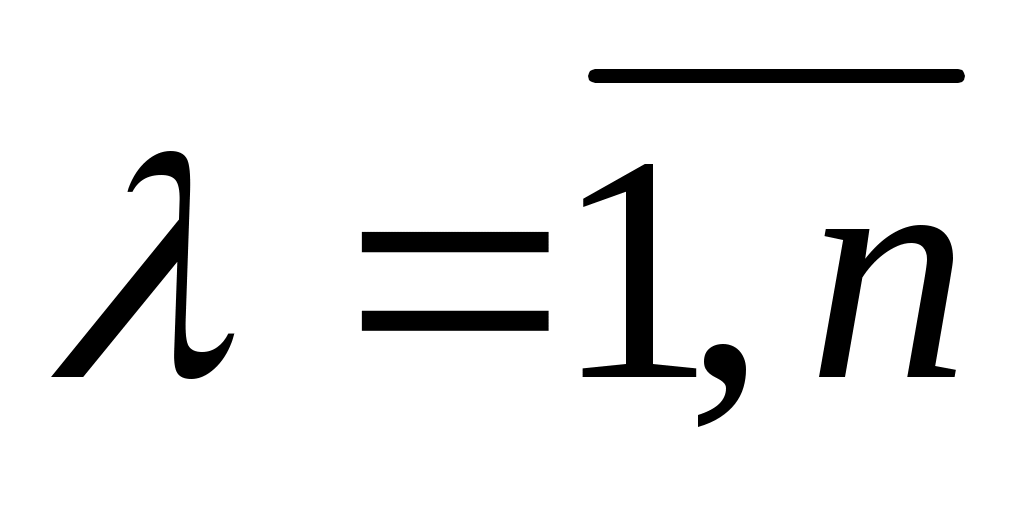 ,
,
при начальных условиях
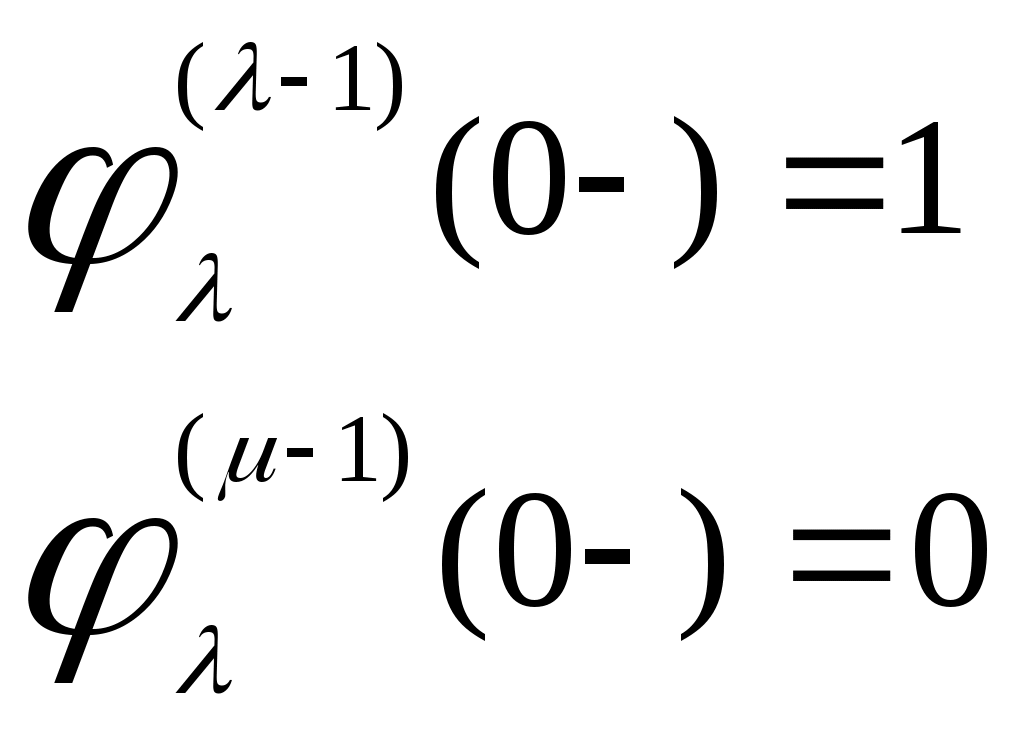 ,
,
для μ ≠ λ; μ,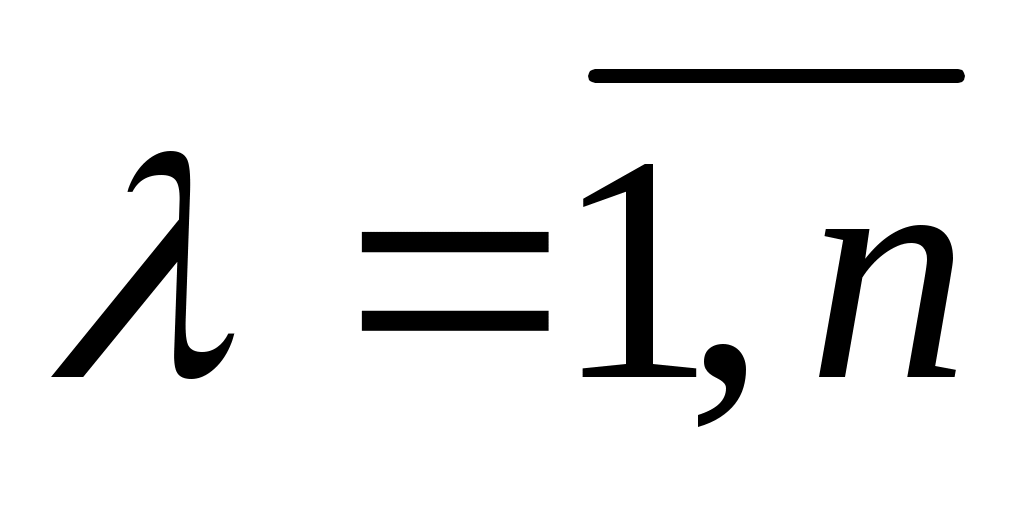 .
.
Это значит, что они представляют собой множество (одностороннее) базисных функций .
.
Отождествим постоянные, появившиеся в (1), с составляющими вектора x(t0) - состоянием в момент времени t0-. Наиболее естественным способом будет отождествление базисных функций с функциями φ1,…, φn в (3). В этом случае составляющие x(t0-), которые представляют собой коэффициенты базисных функций, будут
в момент времени t0-. Наиболее естественным способом будет отождествление базисных функций с функциями φ1,…, φn в (3). В этом случае составляющие x(t0-), которые представляют собой коэффициенты базисных функций, будут
x1(t0-) = y0(t0-),
xn(t0-) = y(n-1)(t0-),
или в более компактной форме
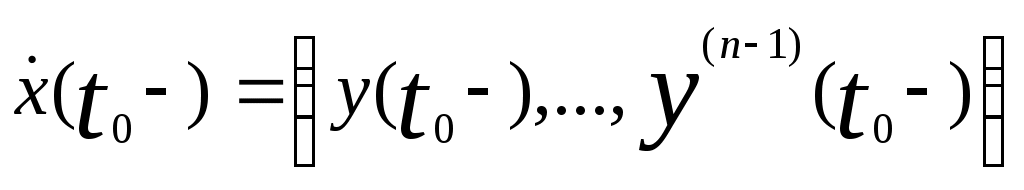 . (4)
. (4)
Другой естественный способ состоит в том, чтобы положить базисные функции, или, точнее, их преобразования по Лапласу, равными
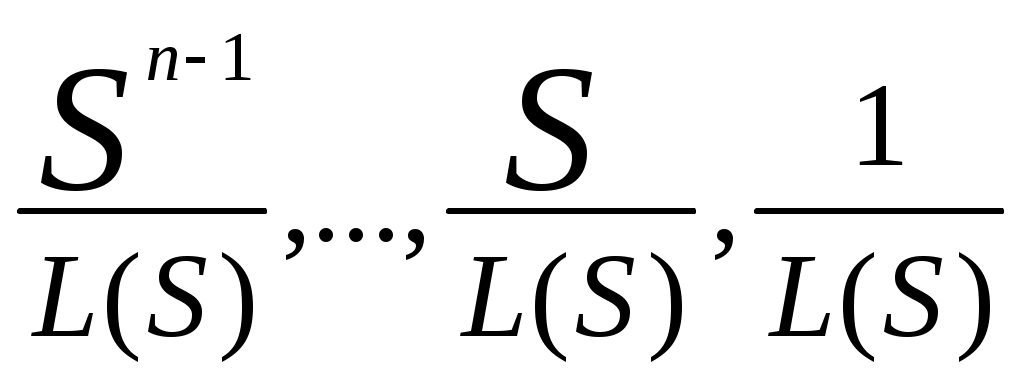 .
.
В этом случае составляющими x(t0) будут
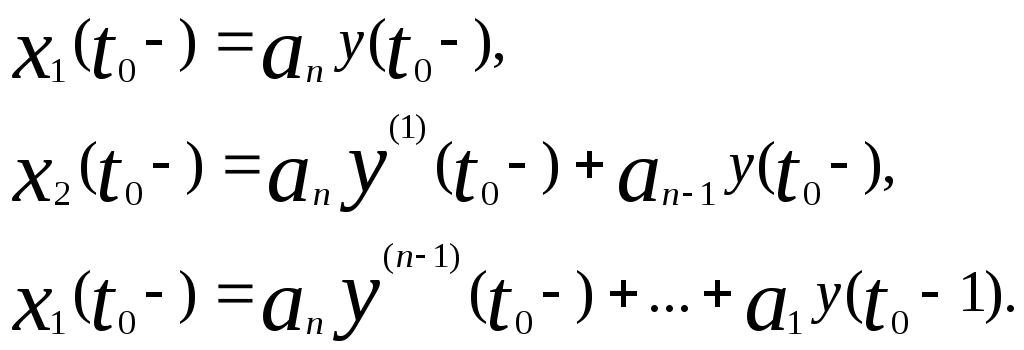 (6)
(6)
Рассмотрим случай, когда первая составляющая начального вектора состояния приравнена к выходу в моменты времени t0-, вторая составляющая – первой производной выхода и т.д. Это значит, что вектор состояния в момент времени t представляется в виде
в моменты времени t0-, вторая составляющая – первой производной выхода и т.д. Это значит, что вектор состояния в момент времени t представляется в виде
x(t) = (y(t),…, y(n-1)(t)). (7)
Ради удобства вектор x(t), определенным с помощью (7), назовем нормальным вектором состояния , а соответствующие уравнения состояния – нормальными уравнениями для
, а соответствующие уравнения состояния – нормальными уравнениями для  . Пространство состояний, которому принадлежат х будет
. Пространство состояний, которому принадлежат х будет 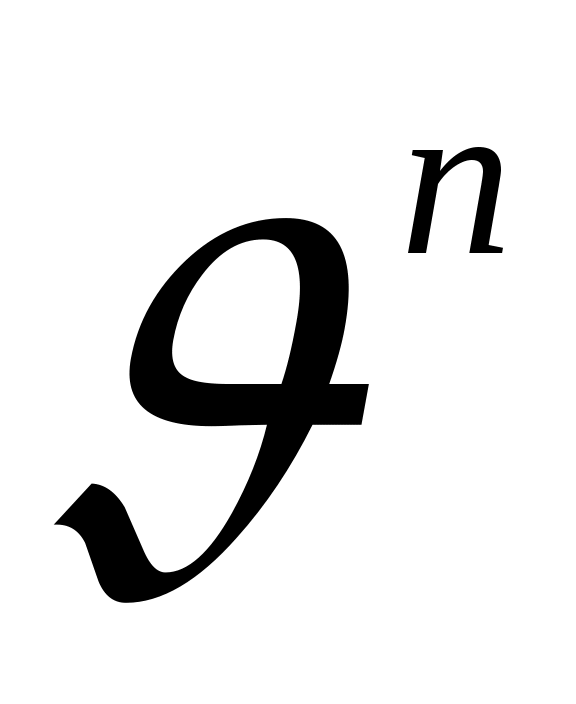
, т.е. пространства упорядоченных наборов по n комплексных чисел.
Чтобы получить уравнение системы найдем выражение
найдем выражение 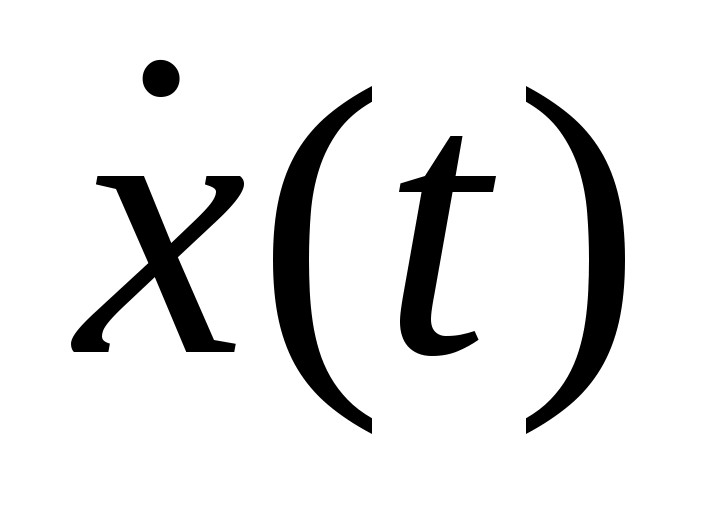 , для чего продифференцируем обе части равенства (7). В результате получим
, для чего продифференцируем обе части равенства (7). В результате получим
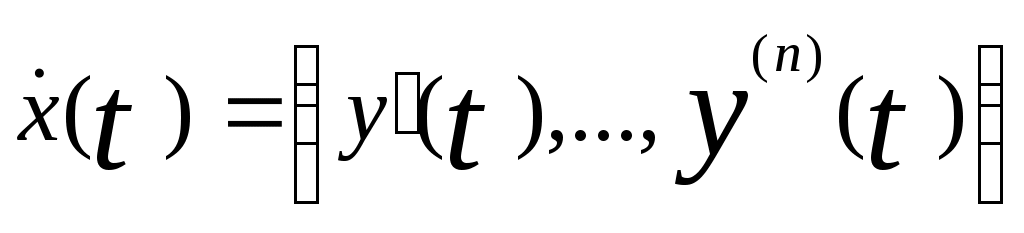 . (8)
. (8)
С другой стороны из дифференциального уравнения (1) следует
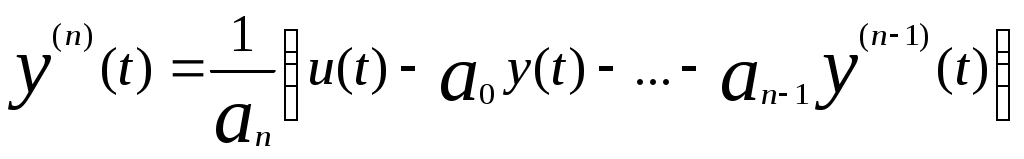
и, следовательно,
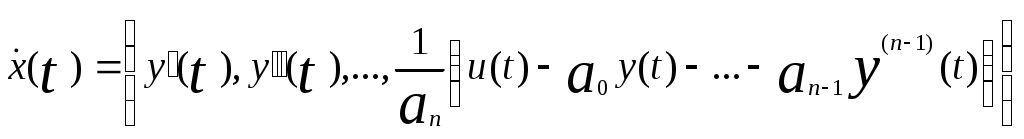 .
.
Это соотношение показывает, что составляющие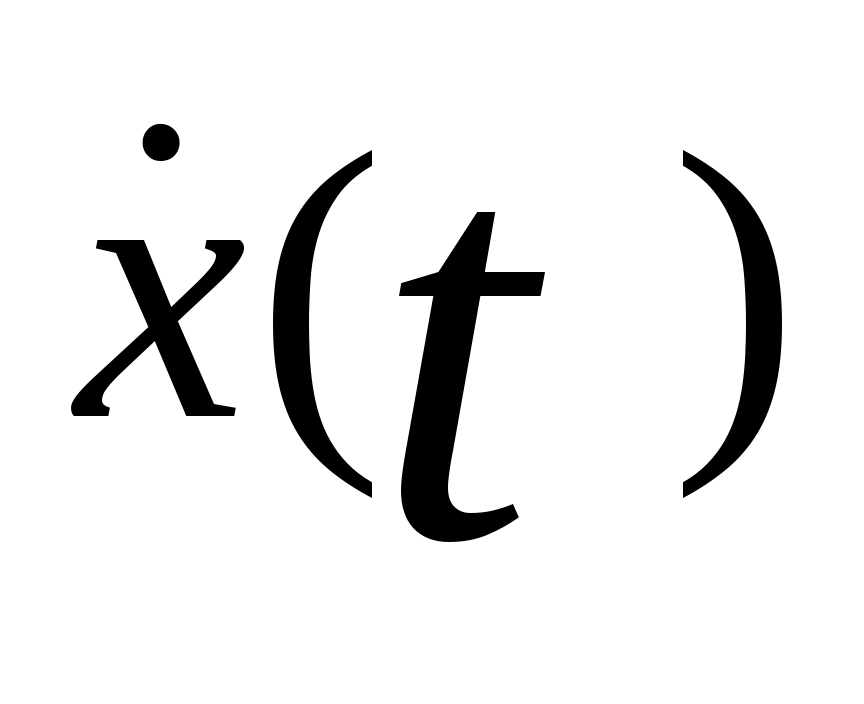 представляют собой линейные комбинации составляющих x(t) и u(t). Для представления этого соотношения в матричной форме обозначим через
представляют собой линейные комбинации составляющих x(t) и u(t). Для представления этого соотношения в матричной форме обозначим через 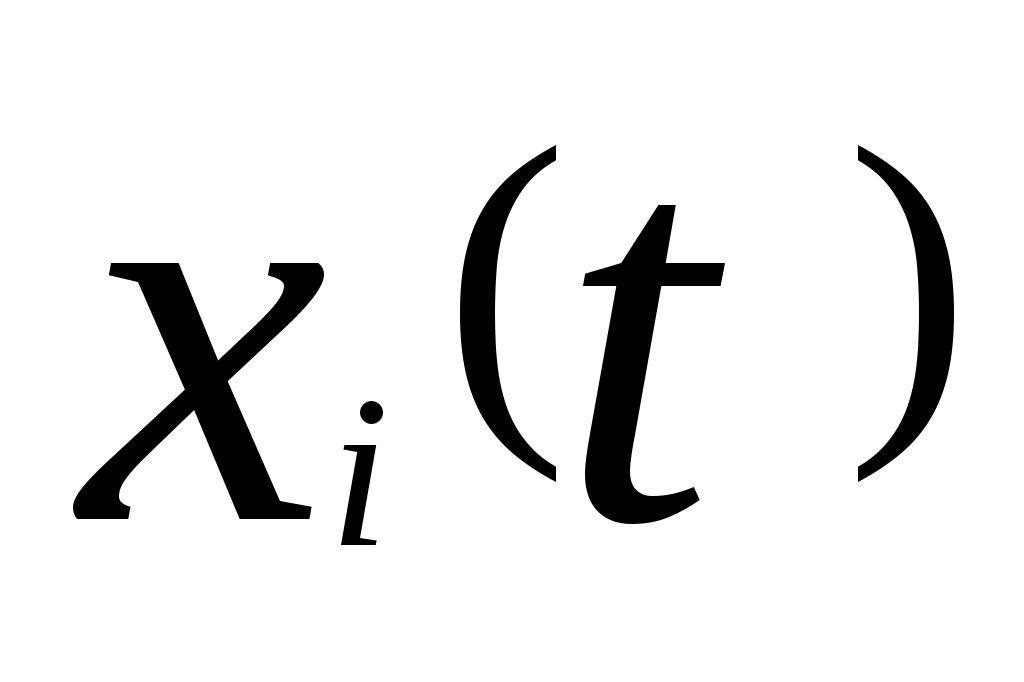 и
и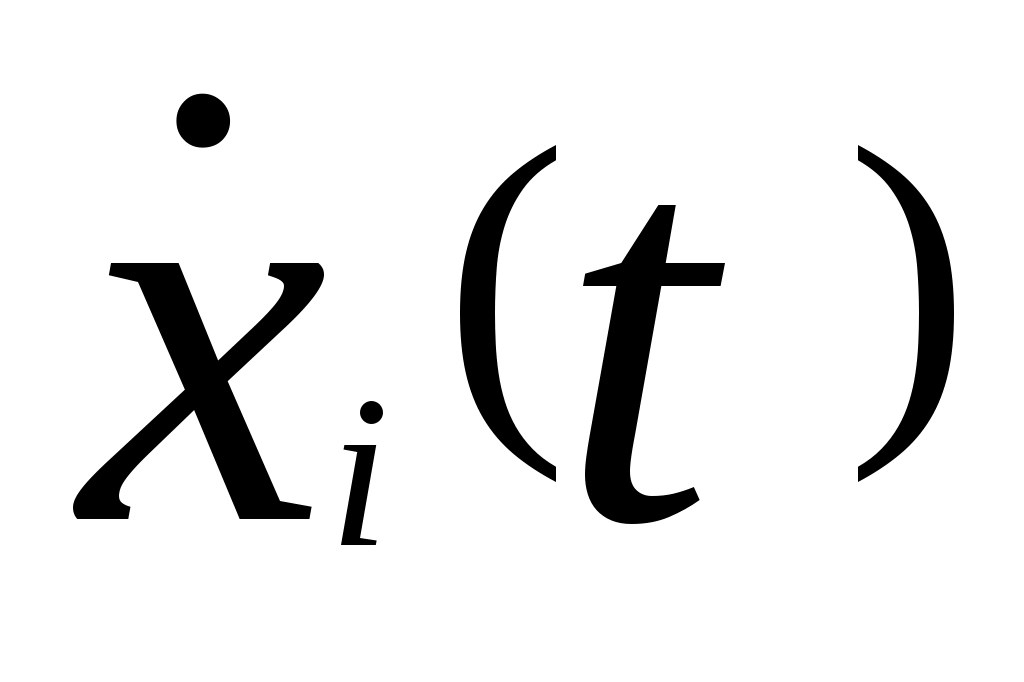 ,
,  , i-ые составляющие
, i-ые составляющие 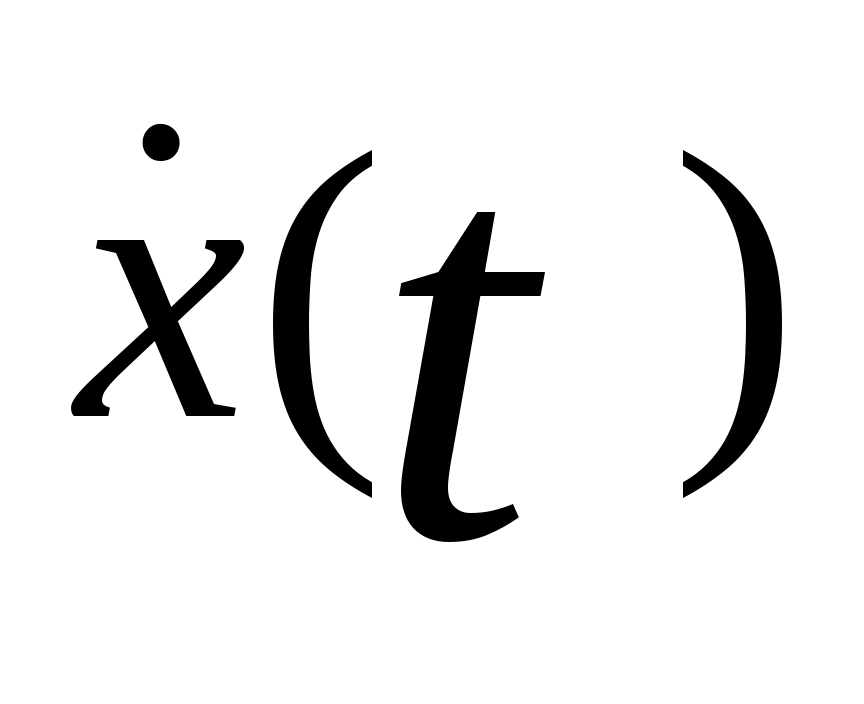 соответственно. Тогда из (8) следует
соответственно. Тогда из (8) следует
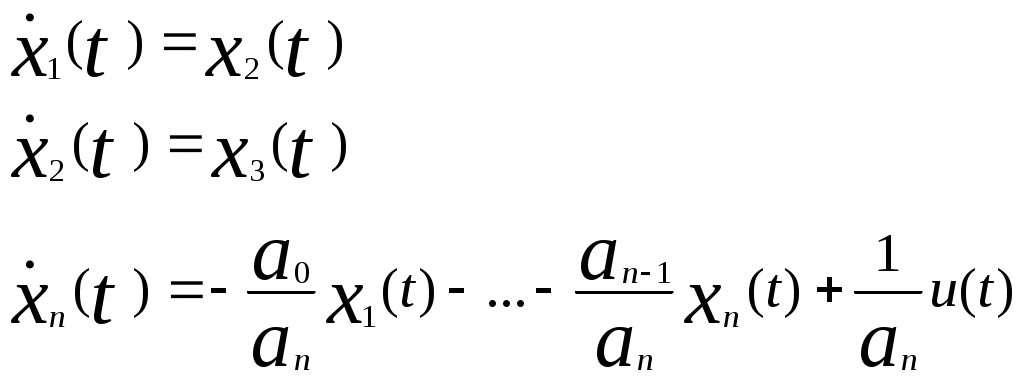
или в матричной форме
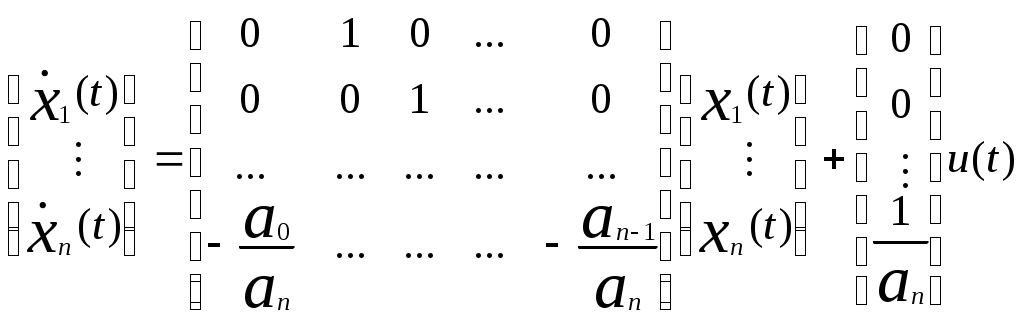 .
.
Последнее соотношение есть уравнение состояния в канонической форме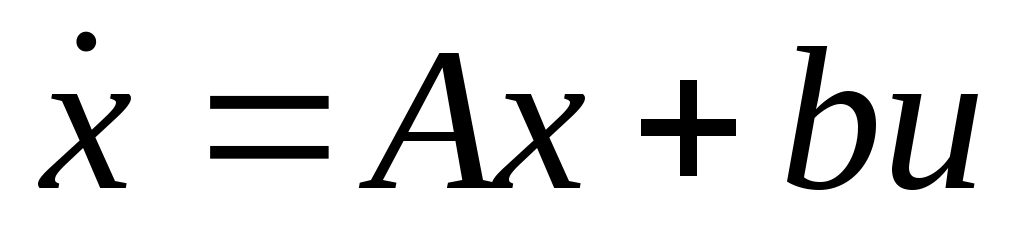 , где А и b представляют собой соответственно, n×n матрицу с постоянными коэффициентами и n-мерный вектор.
, где А и b представляют собой соответственно, n×n матрицу с постоянными коэффициентами и n-мерный вектор.
Таким образом, если x(t) задан с помощью (7), будучи определенным в , то x(t) удовлетворяет уравнению состояния (9). Этот результат совместно с соотношением
, то x(t) удовлетворяет уравнению состояния (9). Этот результат совместно с соотношением
y(t) = x1(t), или в матричной форме
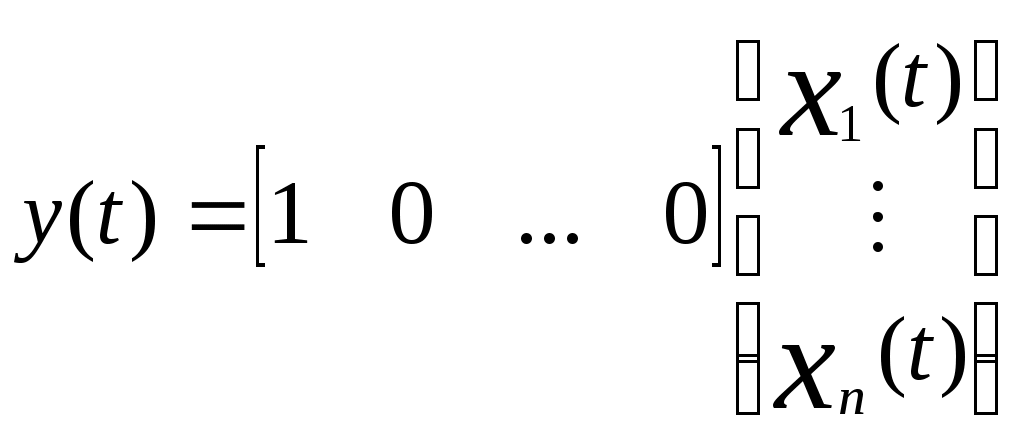 .
.
Пусть - обратно-дифференциально-операторная система, описываемая соотношением вход-выход-состояние
- обратно-дифференциально-операторная система, описываемая соотношением вход-выход-состояние
L(p)y = u, L(p) = anp
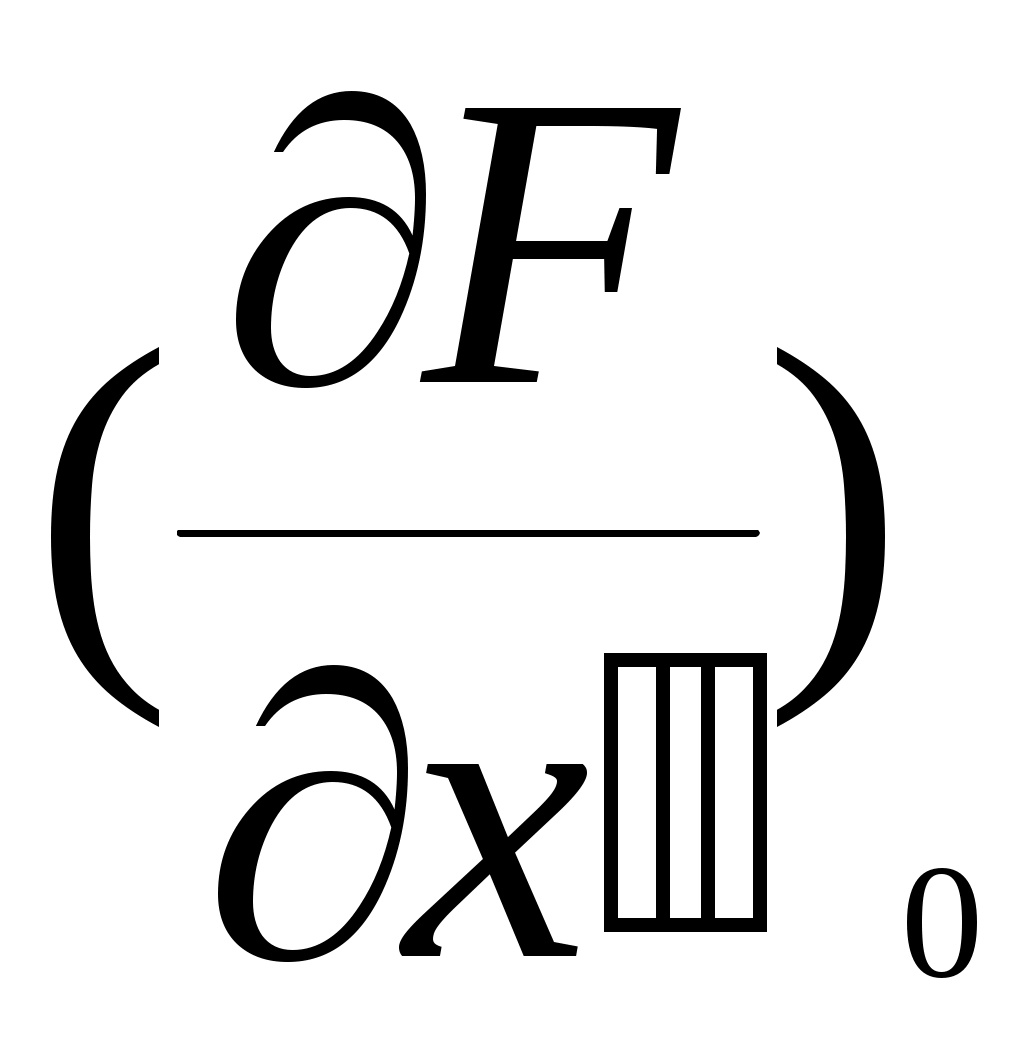 ,
, 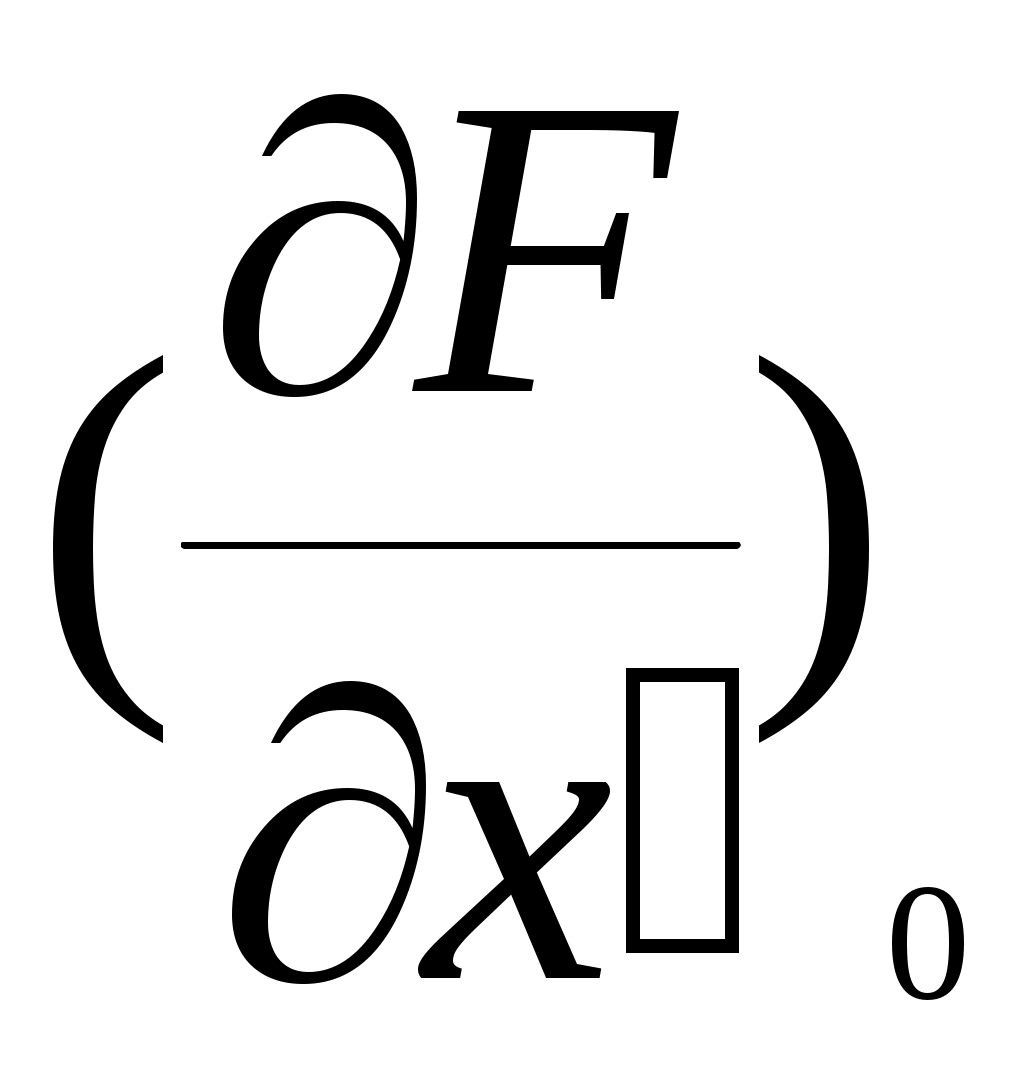 ,
, 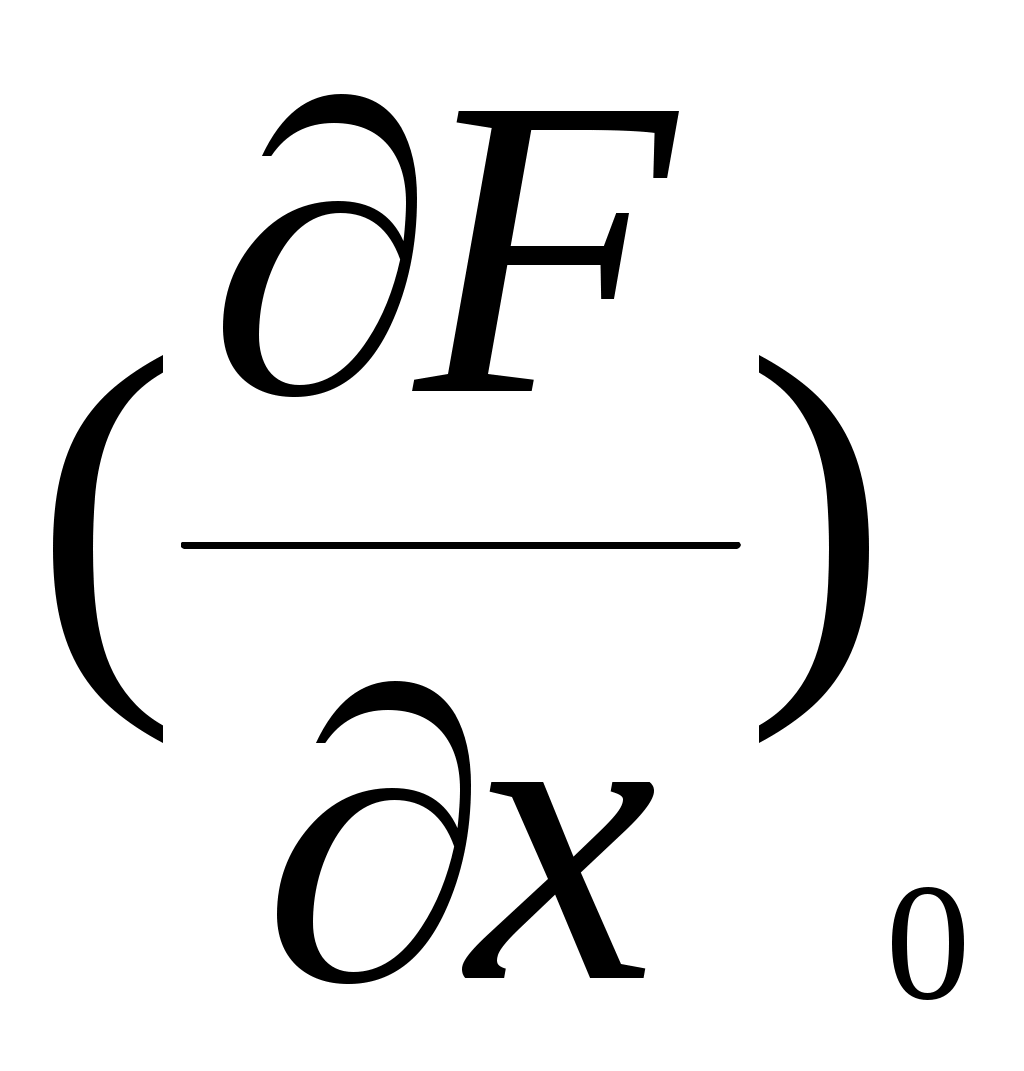 ,
, 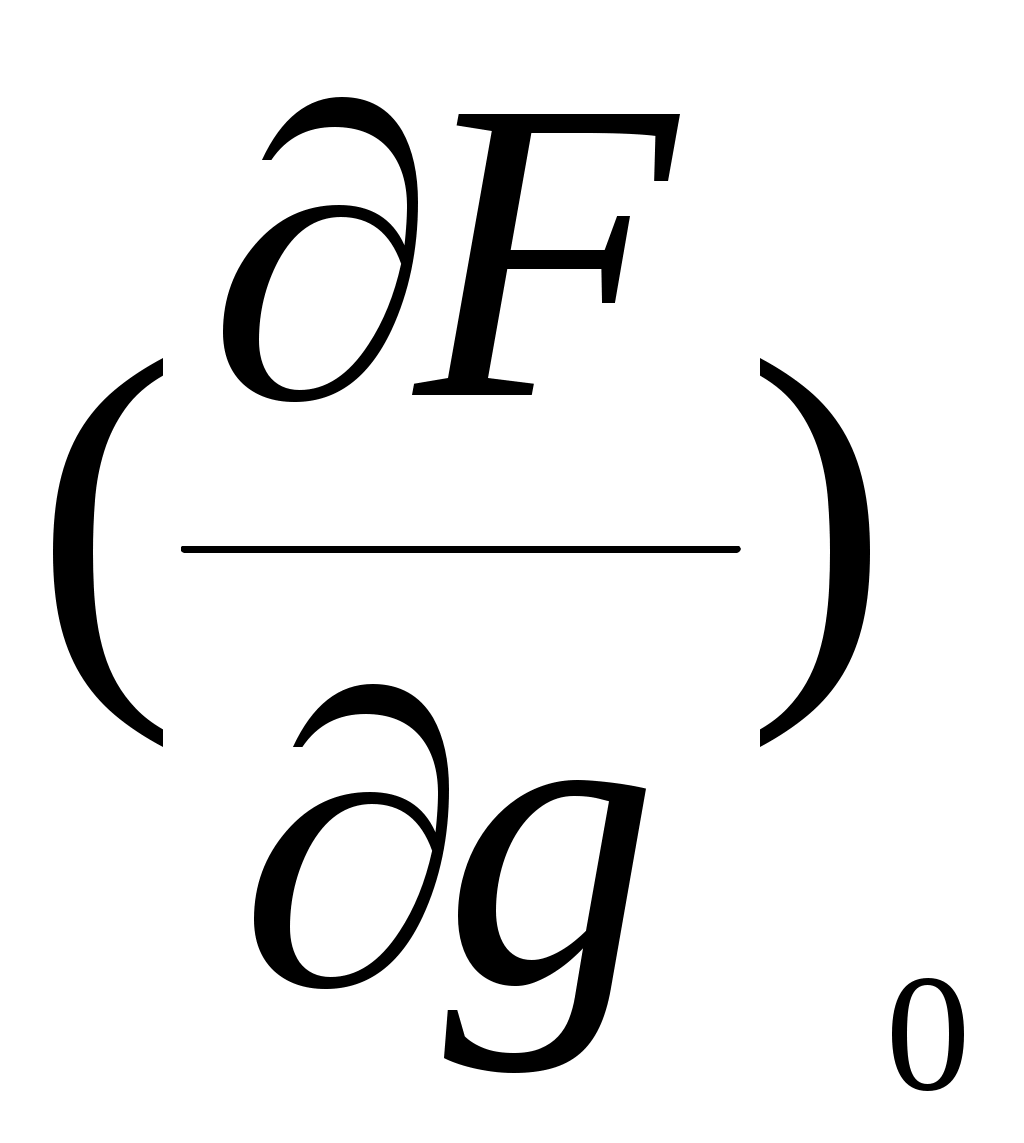 и представляет собой результат линеаризации уравнения (1).
и представляет собой результат линеаризации уравнения (1).Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x’’, x’, x, g) в окрестности точки, соответствующей установившемуся состоянию.
Процесс линеаризации уравнения (1) может быть геометрически интерпретирован следующим образом. В пространстве переменных x’’, x’, x, g уравнение (1) задает некоторую поверхность. Переход от уравнения (1) к линейному уравнению (5) означает замену поверхности некоторой касательной плоскостью, проведенной к поверхности в точке, соответствующей установившемуся состоянию. Естественно, что ошибка при такой замене тем меньше, чем меньше отличаются друг от друга точки поверхности и точки плоскости. Это справедливо лишь в некоторой малой окрестности установившегося состояния.
Понятие пространства состояний
С точки зрения анализа и синтеза систем представляется целесообразным разделить все переменные, характеризующие систему, на три группы:
1) входные переменные или входные воздействия mi, представляющие сигналы, генерируемые системами, внешними по отношению к исследуемой, и влияющие на поведение системы;
2) выходные переменные или переменные, характеризующие реакцию системы yj, позволяющие описать некоторые аспекты поведения системы, представляющие интерес для исследователя;
3) переменные (координаты) состояния или промежуточные переменные xk, характеризующие динамическое поведение исследуемой системы.
Величины mi, yj и xk предполагаются функциями времени. Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа, совокупность выходных переменных – в виде вектора выхода, и совокупность переменных состояния – в виде вектора состояния:
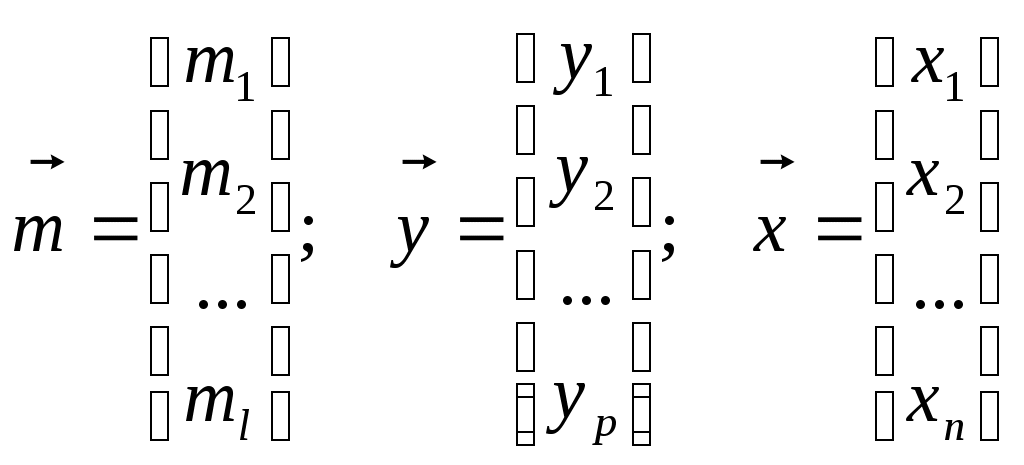 .
.Множество всех значений, которые может принять вектор входа m в момент t, образует пространство входа системы. Множество всех значений, которые может принять вектор выхода y в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы.
Понятие управляемости и наблюдаемости.
Управляемость: Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением
dx(t)/dt=Ax(t)+Dm(t), (1)
где x – n-мерный вектор состояния; m – r-мерный вектор, представляющий управляющие воздействия; A – квадратная матрица коэффициентов n-го порядка; D – матрица управления размера nxr.
Матрица A может быть приведена к диагональной матрице (или в общем случае к жордановой форме)
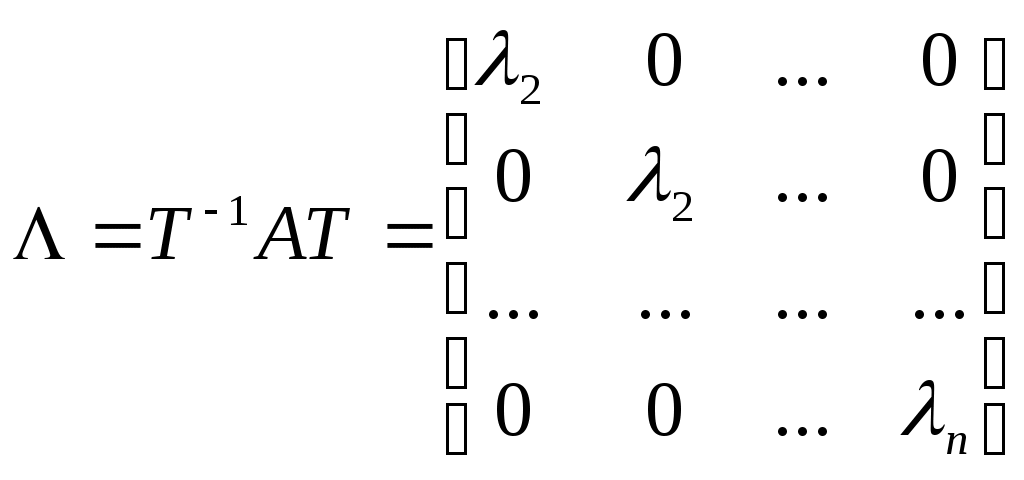
где ш – собственные значения матрицы A, которые предполагаются все различными.
Применяя подстановку x=Tz, исходное уравнение запишется в канонической форме
dz(t)/dt=z(t)+m(t),
где D=T-1D=[ij]nxr.
Вектор z в полученной формуле будем называть каноническим вектором состояния. Будем считать, что в предыдущих матричных выражениях собственные значения li расположены в порядке возрастания их модулей, комплексные li – в порядке возрастания их аргументов, векторы-столбцы матрицы T – нормализованы, то есть выбраны так, что евклидова длина их равна единице.
Запишем полученное выражение в развернутой форме, то есть в виде системы дифференциальных уравнений первого порядка:
Эти уравнения показывают, что управляющее воздействие mk не будет оказывать какого-нибудь влияния на движение по координате zj, если
то есть когда jk=0 для k=1, 2, …, r. Запись в такой форме означает, что все элементы j-й строки матрицы D все равны нулю. Отсюда следует вывод, что неуправляемыми координатами системы являются все те канонические координаты, которые соответствуют нулевым строкам матрицы D. Равенство нулю всех элементов этих строк матрицы D делает невозможным управление по соответствующим координатам. Это означает также, что изменение координат происходит независимо от управляющих воздействий и, следовательно, целиком определяется начальными условиями и возмущениями. Можно сказать, что эти координаты развязаны от управления.
Приведенное рассмотрение позволяет дать следующее определение управляемости: процесс, описываемый уравнением (1), является полностью управляемым, если матрица
D не содержит строк, элементы которых равны нулю; координаты, соответствующие ненулевым строкам D, считаются управляемыми.
Наблюдаемость: Перепишем еще раз выражение для вектора выхода линейного многомерного процесса:
y(t)=Bx(t)+Gm(t), (1)
где y – p-мерный вектор, представляющий выходные переменные; B – матрица выхода размером pxn; G – матрица обхода системы размера pxr.
Пусть матрица B имеет вид
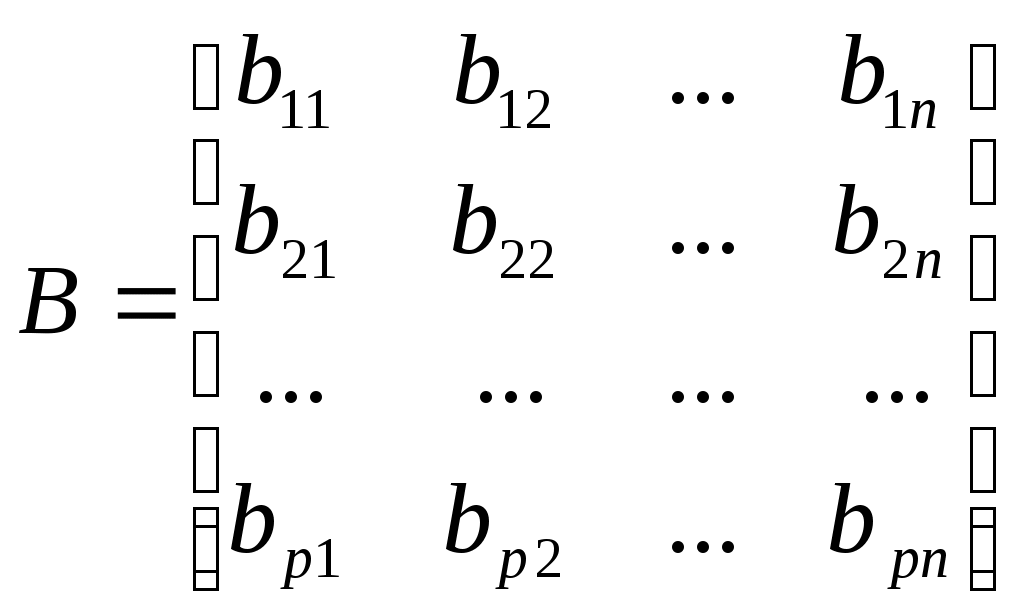
а матрица обхода G задана в виде
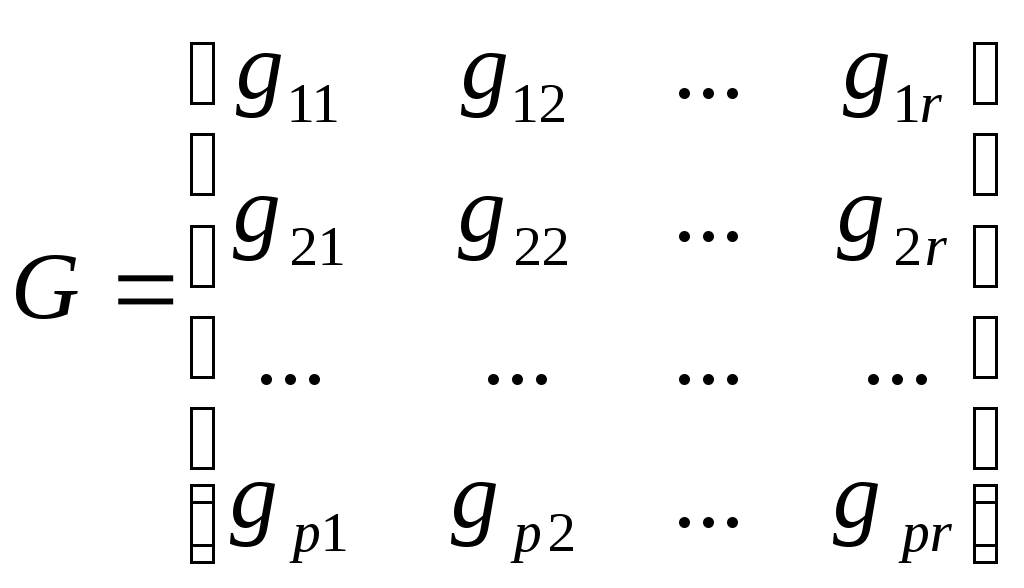
Тогда, развертывая формулу (1), получаем p выражений
Координату состояния принято называть наблюдаемой, если она может быть определена или для нее может быть получена оценка по измеримым выходным переменным. Анализ уравнений (2) показывает, что координата xk может быть определена или для нее может быть получена оценка по измеримым выходным переменным y1, y2, …, yi, …, yp, если коэффициенты bik для i=1, 2, …, p не все равны нулю. Другими словами, xk является наблюдаемой координатой, если элементы k-го столбца матрицы выхода не все равны нулю. Если это условие не соблюдается, то координату xk называют ненаблюдаемой. Таким образом, линейный процесс является наблюдаемым, если матрица выхода B не содержит столбцов, элементы которых равны нулю.
Соотношения вход – состояние – выход
Пусть R – система, описываемая соотношением вход-выход вида
L(p)y = u1 (1),
где L(p) = anpn +…+ a0, an≠0 и ai,
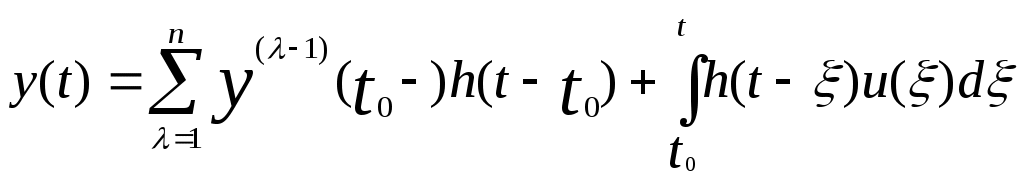 , t ≥ t0 (2)
, t ≥ t0 (2)где
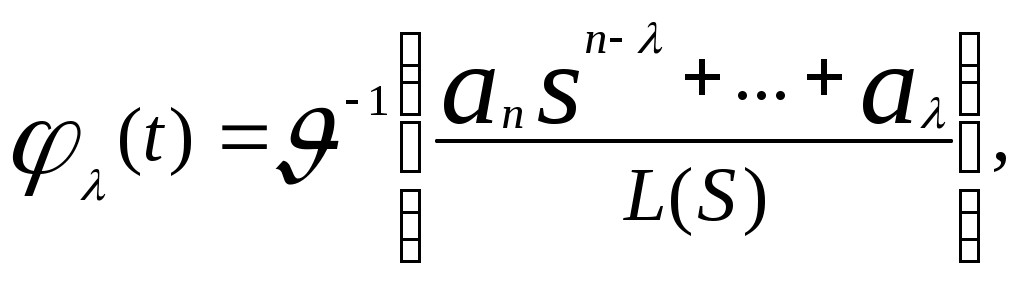
Функции времени φ1,…, φn линейно независимые и удовлетворяют условию (дифференциальному уравнению)
L(p) φλ(t) = 0,
при начальных условиях
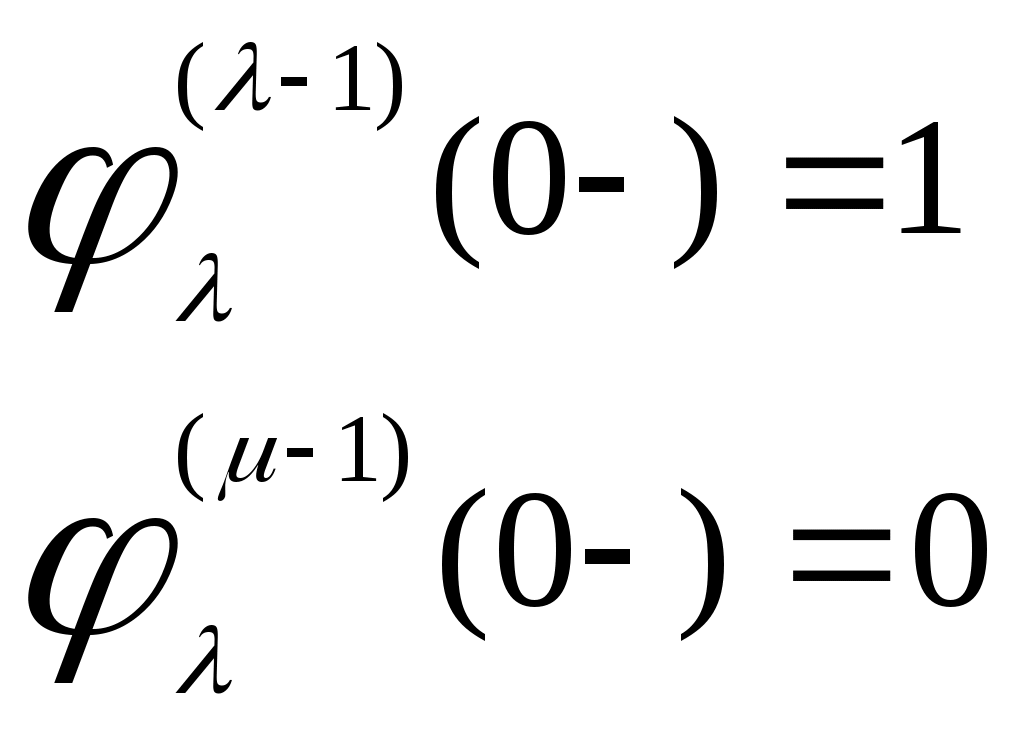 ,
,для μ ≠ λ; μ,
Это значит, что они представляют собой множество (одностороннее) базисных функций
Отождествим постоянные, появившиеся в (1), с составляющими вектора x(t0) - состоянием
x1(t0-) = y0(t0-),
xn(t0-) = y(n-1)(t0-),
или в более компактной форме
Другой естественный способ состоит в том, чтобы положить базисные функции, или, точнее, их преобразования по Лапласу, равными
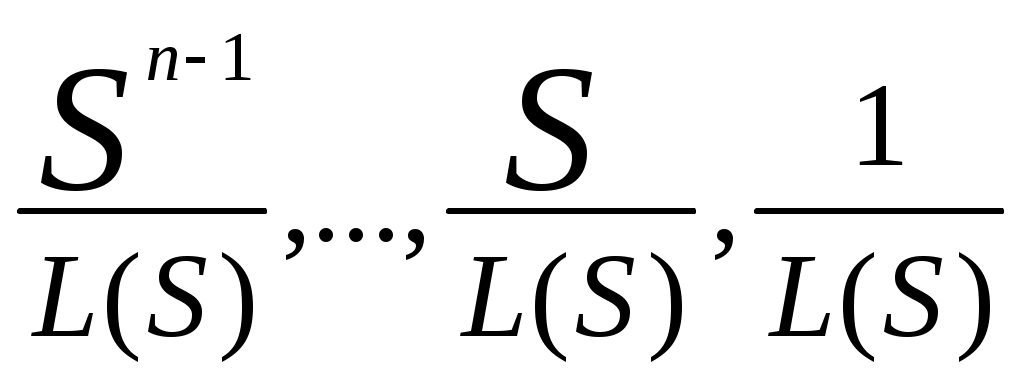 .
.В этом случае составляющими x(t0) будут
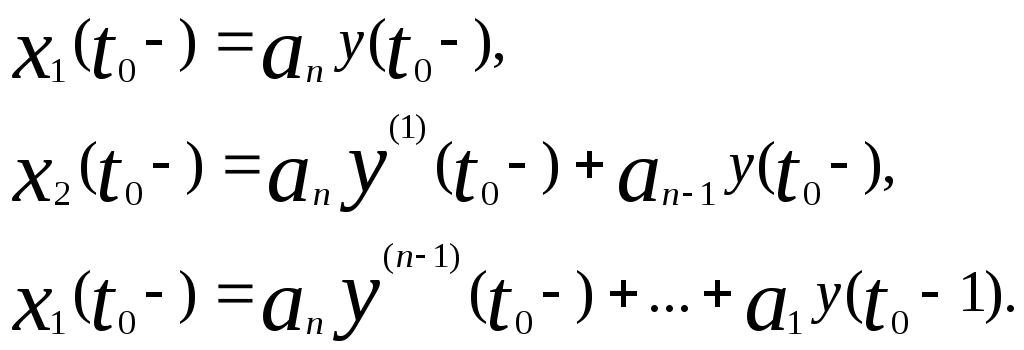 (6)
(6)Рассмотрим случай, когда первая составляющая начального вектора состояния приравнена к выходу
x(t) = (y(t),…, y(n-1)(t)). (7)
Ради удобства вектор x(t), определенным с помощью (7), назовем нормальным вектором состояния
, т.е. пространства упорядоченных наборов по n комплексных чисел.
Уравнения состояния.
Чтобы получить уравнение системы
С другой стороны из дифференциального уравнения (1) следует
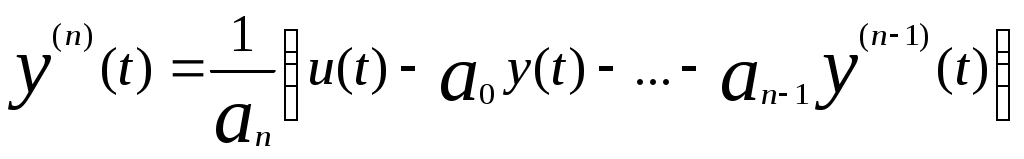
и, следовательно,
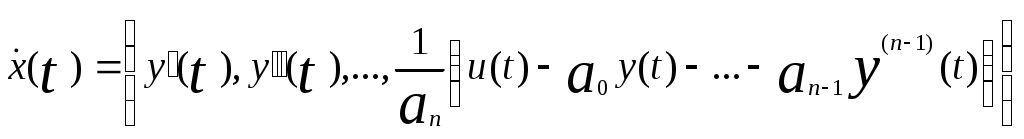 .
.Это соотношение показывает, что составляющие
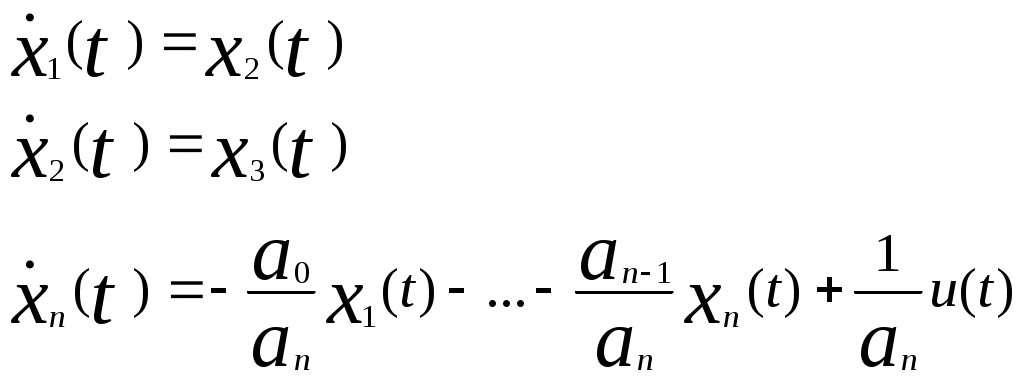
или в матричной форме
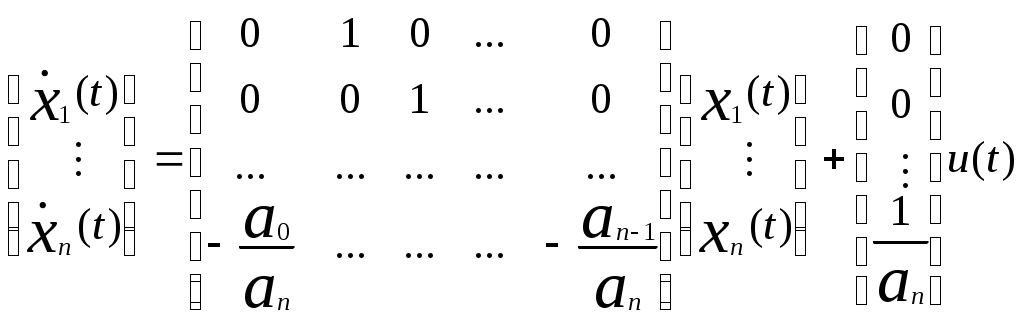 .
.Последнее соотношение есть уравнение состояния в канонической форме
Таким образом, если x(t) задан с помощью (7), будучи определенным в
y(t) = x1(t), или в матричной форме
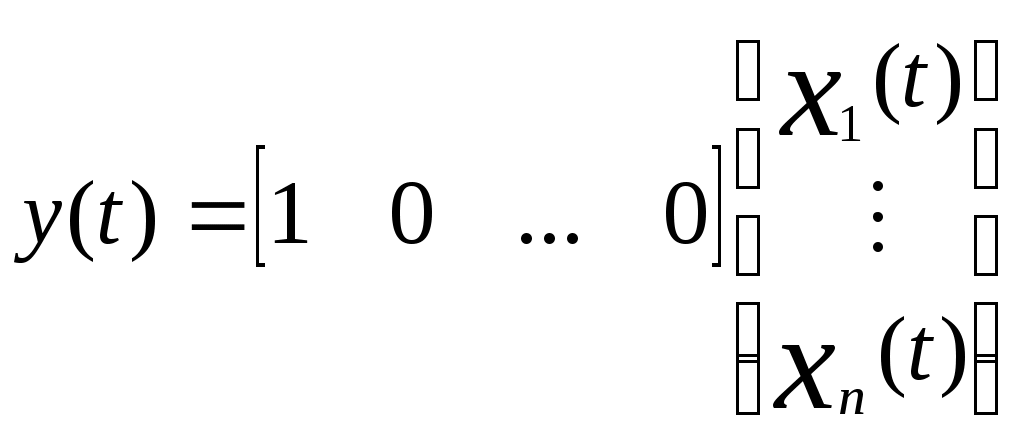 .
.Пусть
L(p)y = u, L(p) = anp