Добавлен: 10.11.2023
Просмотров: 78
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Понятие дифференциального уравнения
Представление непрерывных систем в виде дифференциальных уравнений.
Преобразование системы дифференциальных уравнений.
Основные свойства линейных дифференциальных уравнений.
Решение дифференциальных уравнений первого порядка
Общее решение линейной однородной системы
Линейная неоднородная система. Метод вариации произвольных постоянных.
Дифференциальные уравнения систем автоматического регулирования.
Методика составления дифференциальных уравнений систем автоматического регулирования.
n +…+ a0, an≠0
Тогда вектор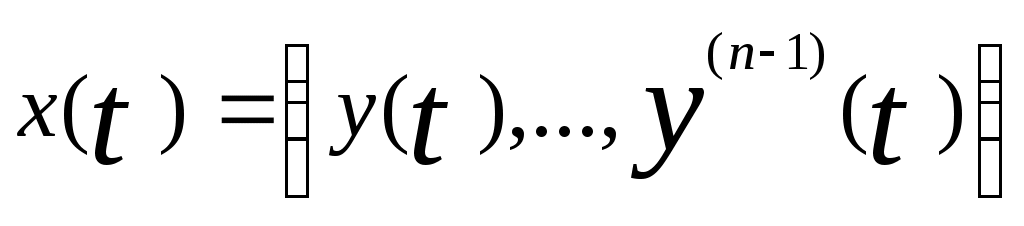
будет вектором состояния системы 
в момент времени t. При таком выборе x(t) уравнение для будет
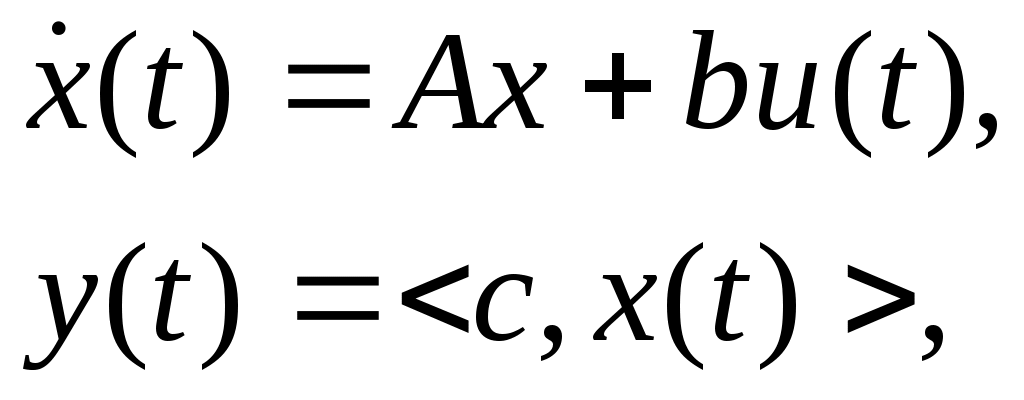(10)
где
, 
.
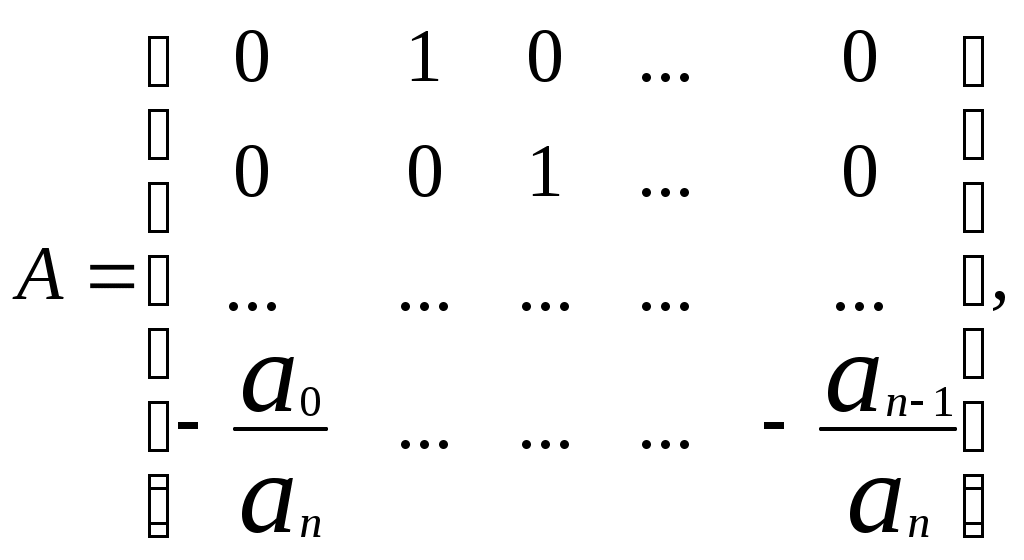
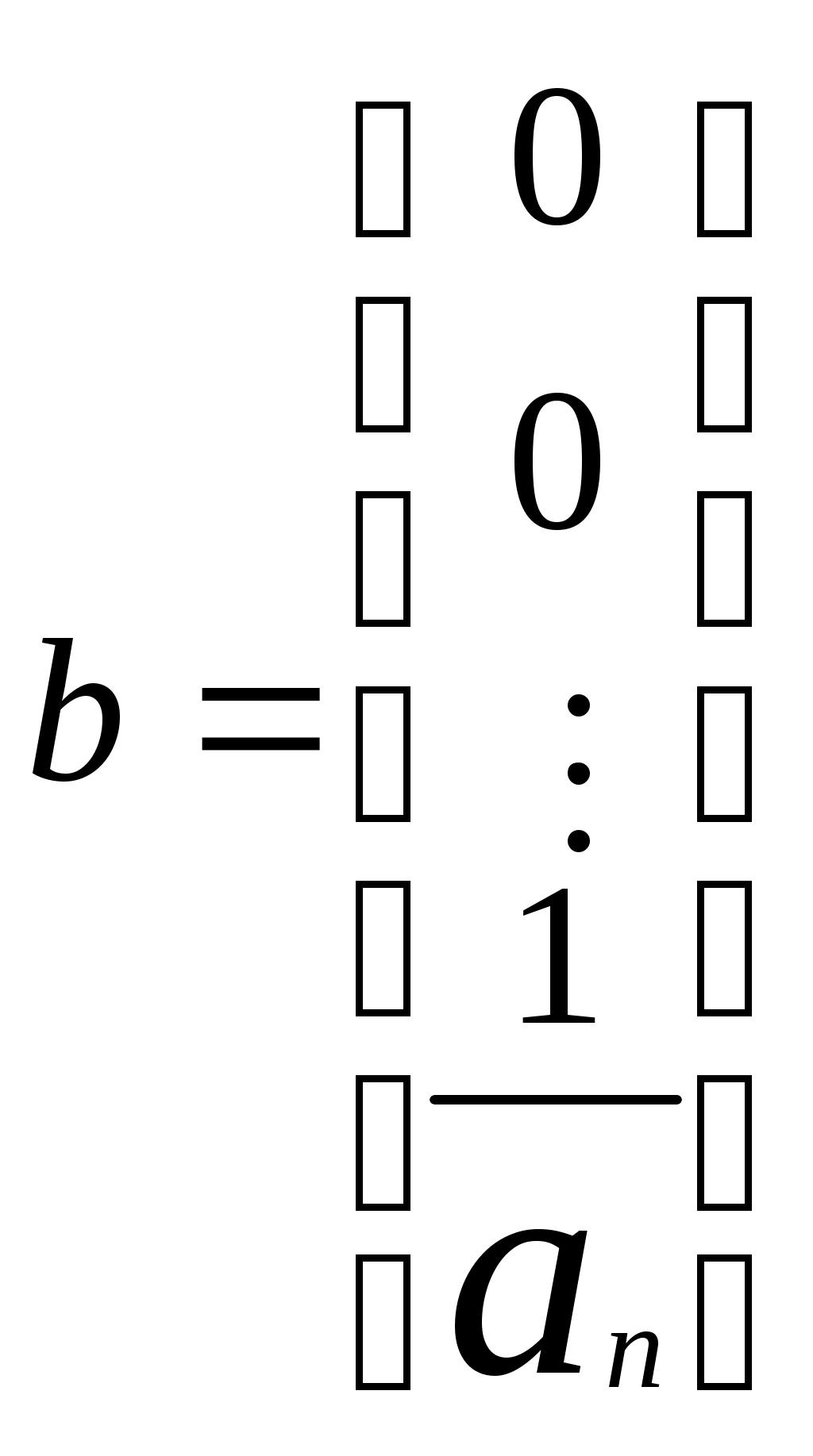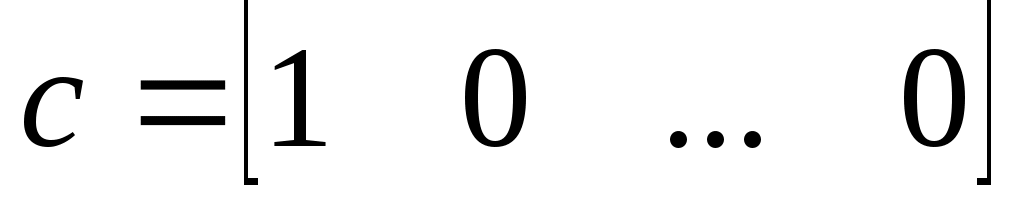Соотношение вход-выход-состояние для будет
(11)
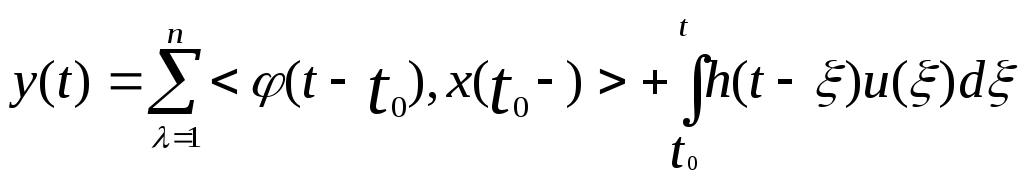, t ≥ t0
где
.
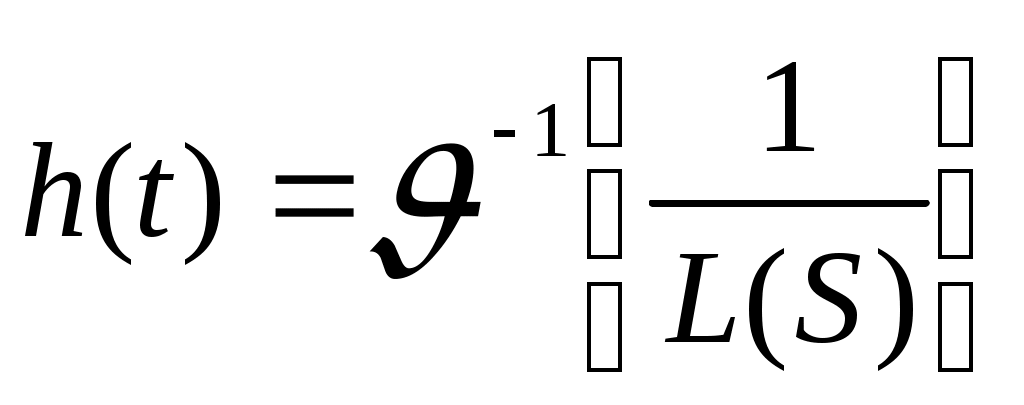
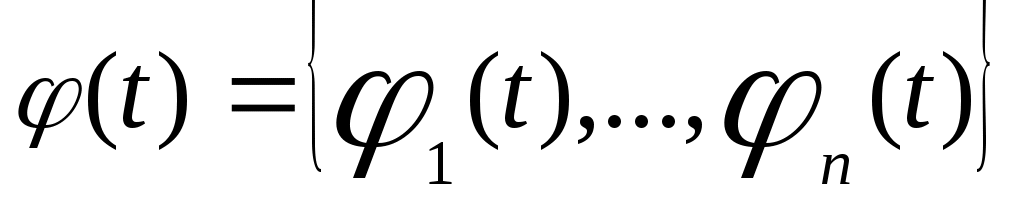
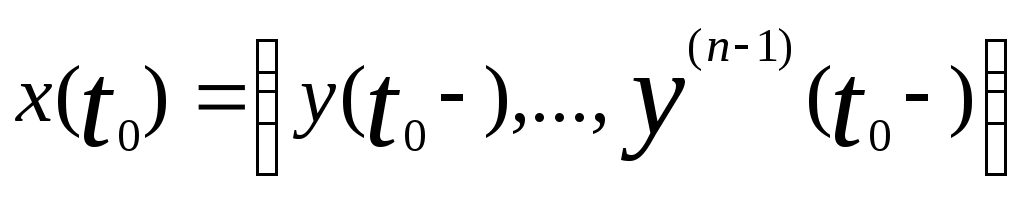Пример:
Допустим, что система описывается уравнением
.
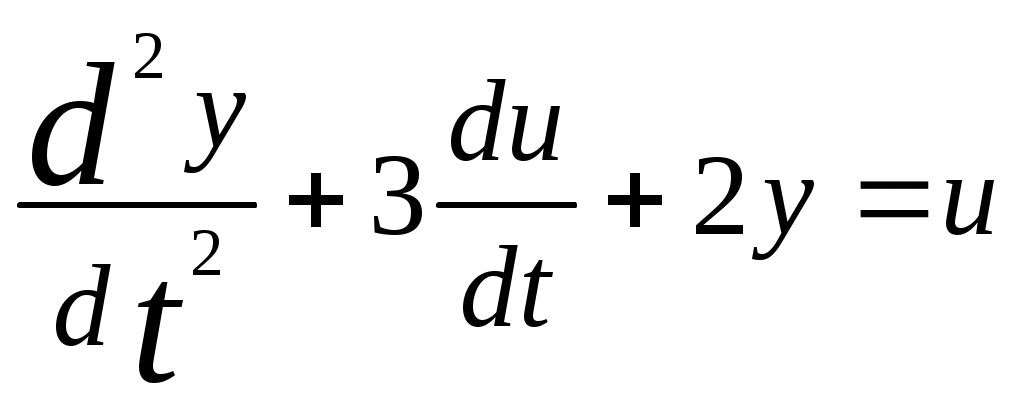Тогда L(S) = S2 + 3S + 2 = (S+1)(S+2)
и
,
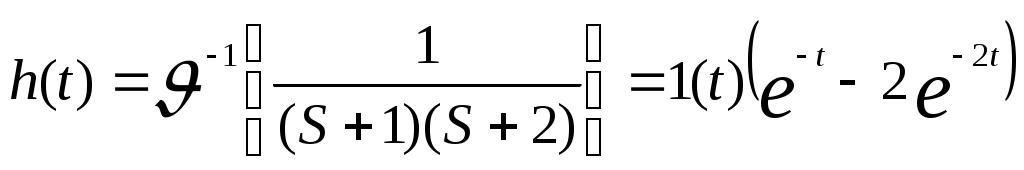
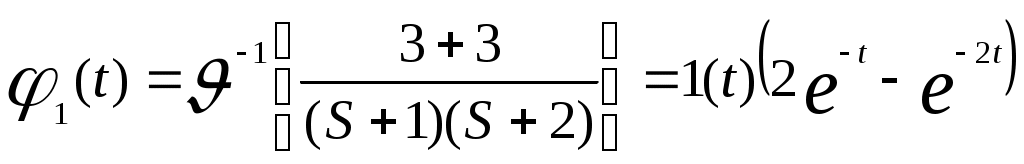
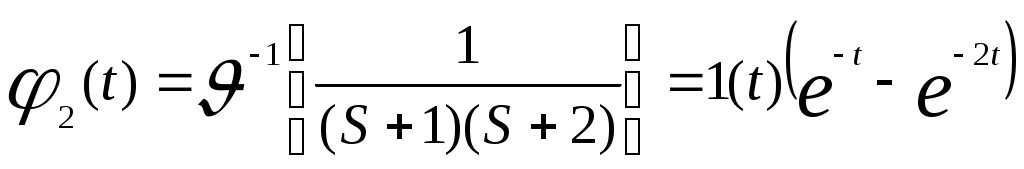где 1(t) обозначает единичную функцию.
Соответствующие вектора состояния в момент времени t будут
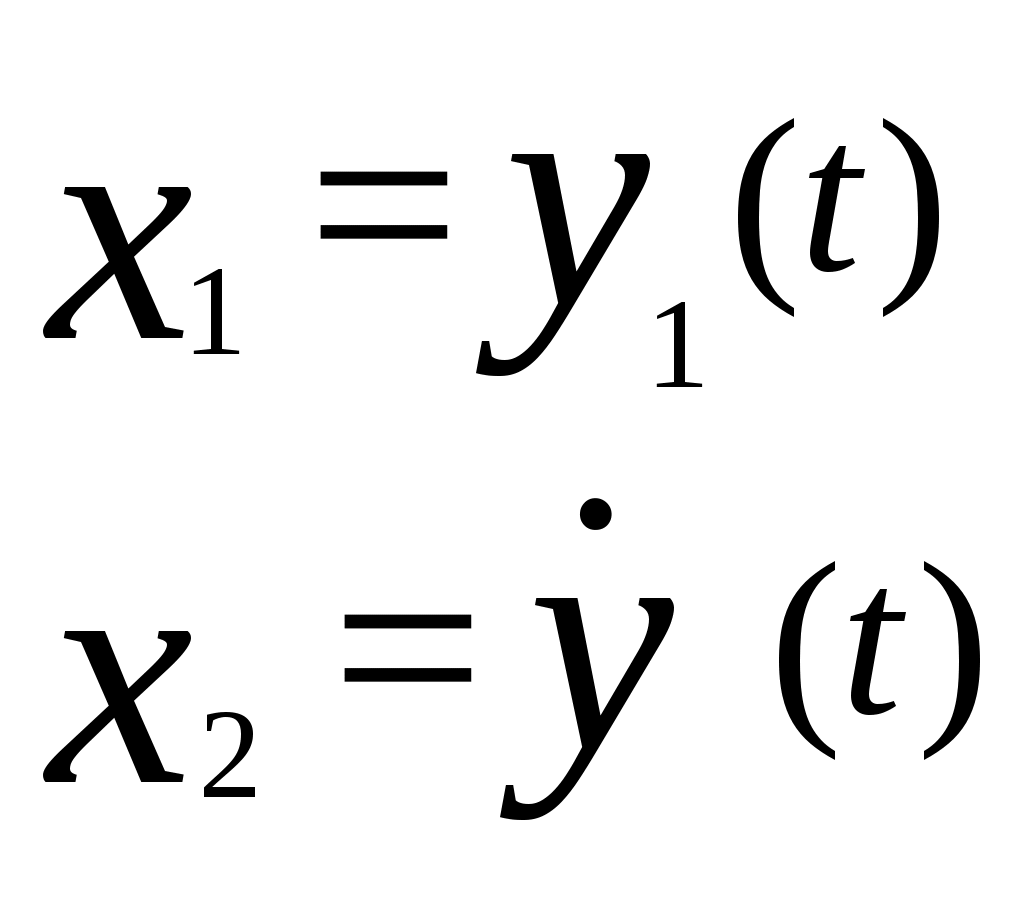
Соответственно соотношение вход-выход-состояние можно записать в виде
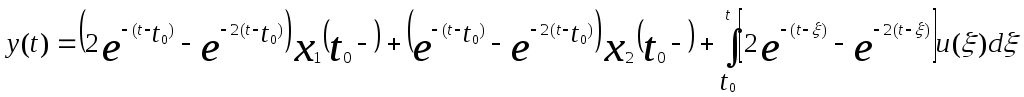, t ≥ t0,
а матрицы и векторы будут
, 
,
.
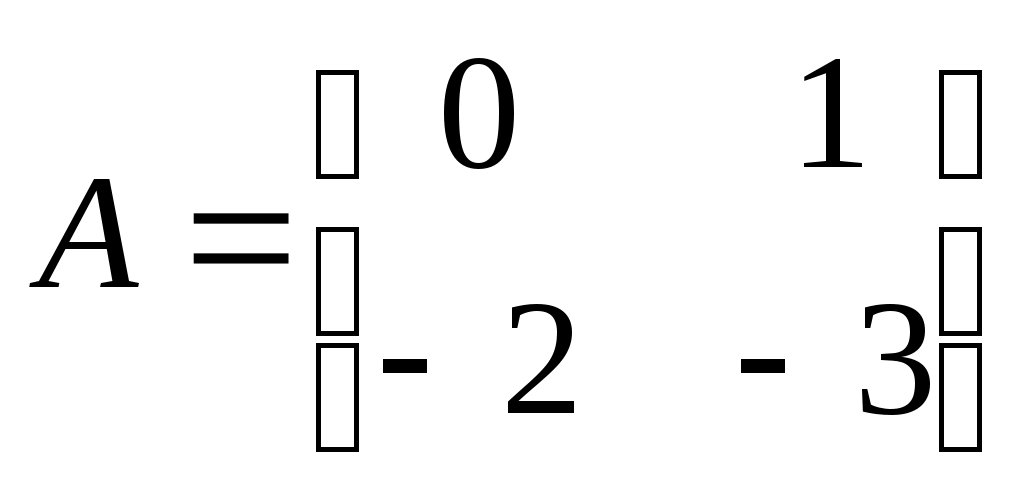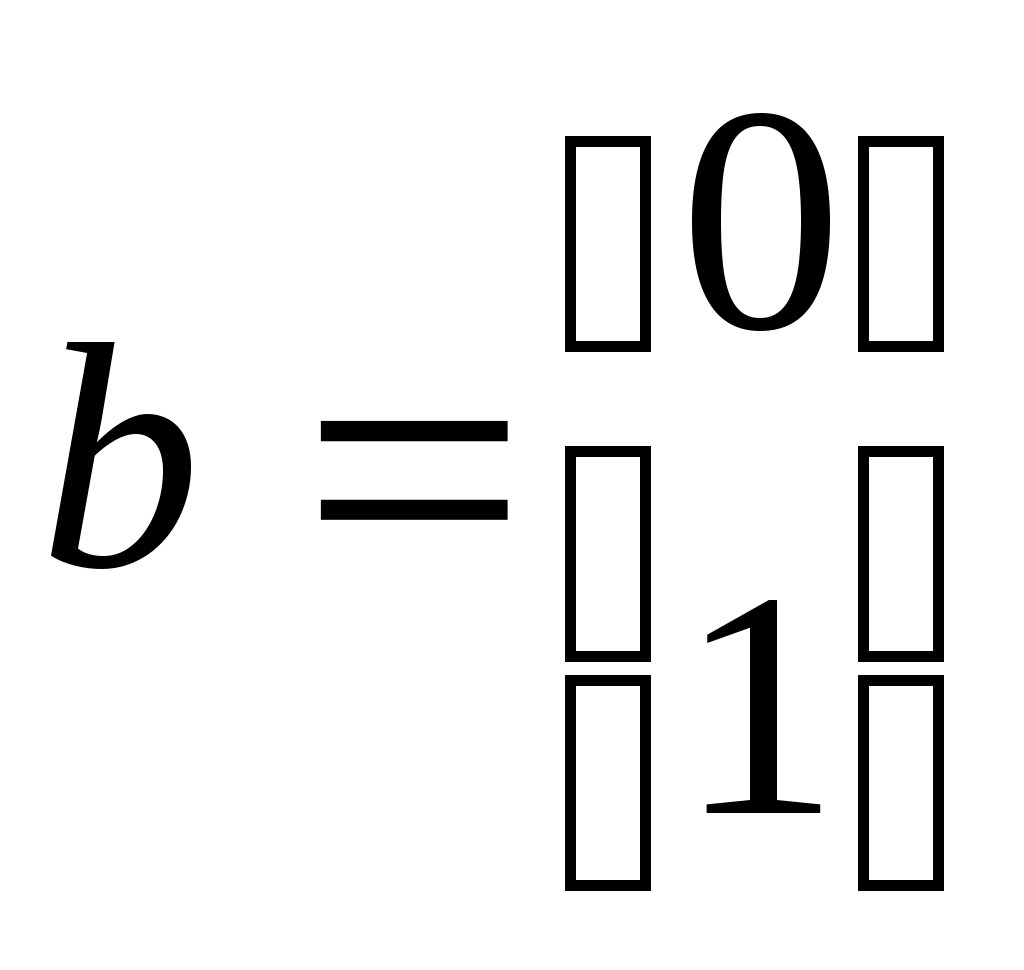
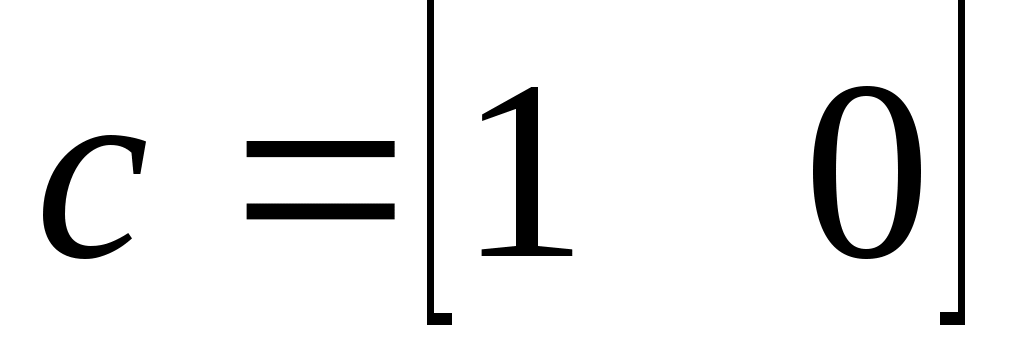Список литературы.
Веретенников, В. Н. Обыкновенные дифференциальные уравнения : учебное пособие : [16+] / В. Н. Веретенников. – Москва ; Берлин : Директ-Медиа, 2020. – Ч. 1. – 96 с.
Будак, Б. А. Математика: сборник задач по углублённому курсу : [12+] / Б. А. Будак, Н. Д. Золотарева, Ю. А. Попов ; под ред. М. В. Федотова. – 5-е изд., электрон. – Москва : Лаборатория знаний, 2020. – 329 с.
Абрамян, М. Э. Лекции по дифференциальному исчислению функций одной переменной : учебник : [16+] / М. Э. Абрамян ; Южный федеральный университет. – Ростов-на-Дону ; Таганрог : Южный федеральный университет, 2020. – 228 с.
Осипенко, С. А. Элементы высшей математики : учебное пособие : [16+] / С. А. Осипенко. – Москва ; Берлин : Директ-Медиа, 2020. – 202 с.
Вагин, Д. В. Численное моделирование динамических систем, описываемых обыкновенными дифференциальными уравнениями : учебное пособие : [16+] / Д. В. Вагин ; Новосибирский государственный технический университет. – Новосибирск : Новосибирский государственный технический университет, 2019. – 63 с.
Тогда вектор
будет вектором состояния системы в момент времени t. При таком выборе x(t) уравнение для будет (10)где
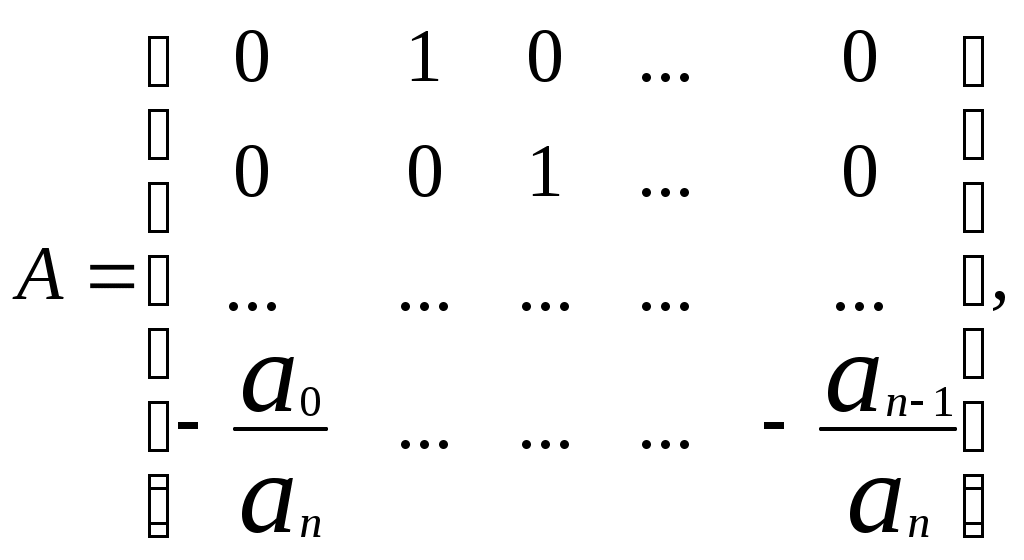
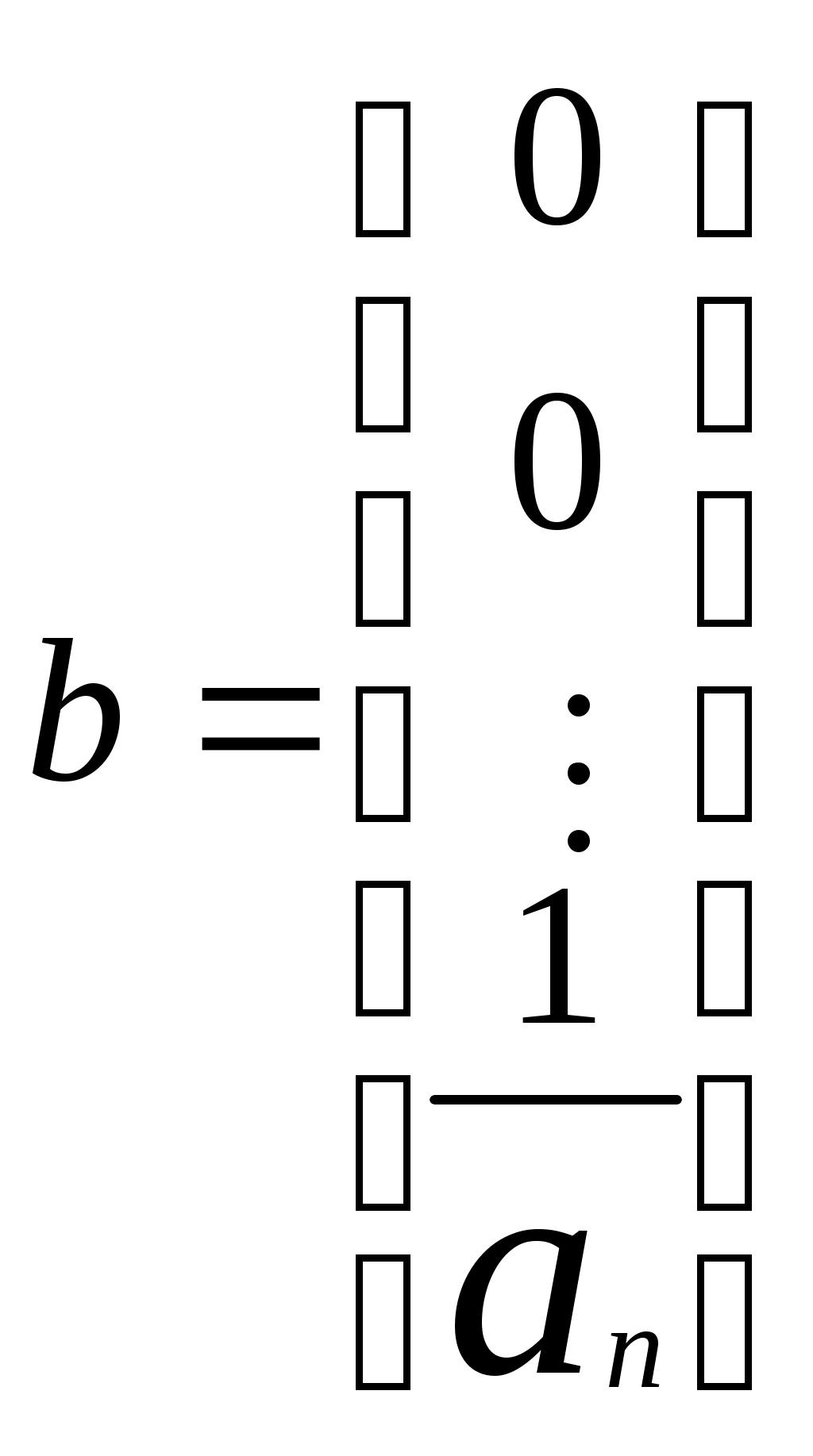, .Соотношение вход-выход-состояние для
будет(11)
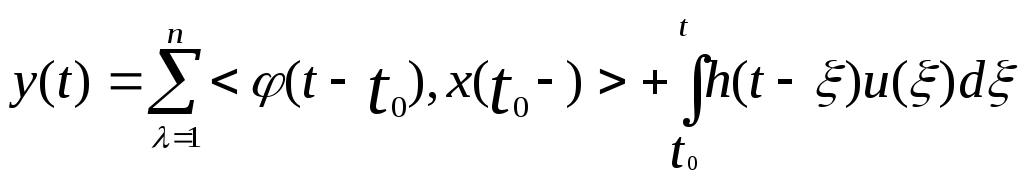, t ≥ t0где
.Пример:
Допустим, что система описывается уравнением
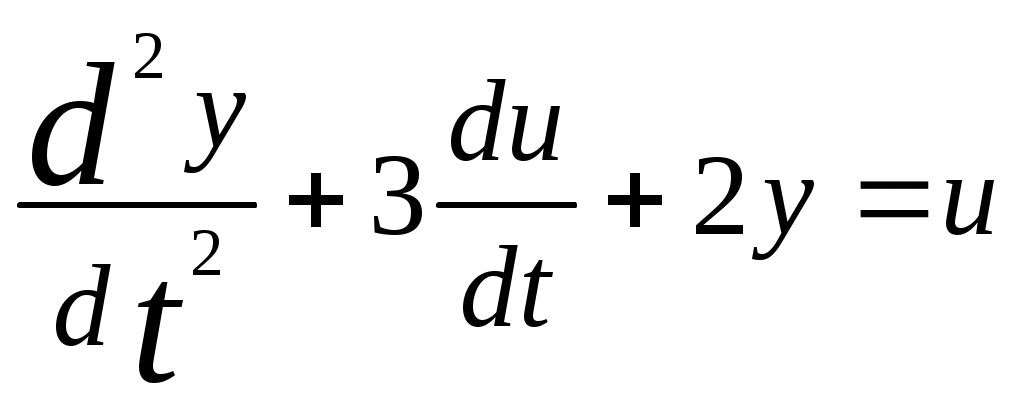.Тогда L(S) = S2 + 3S + 2 = (S+1)(S+2)
и
,где 1(t) обозначает единичную функцию.
Соответствующие вектора состояния в момент времени t будут
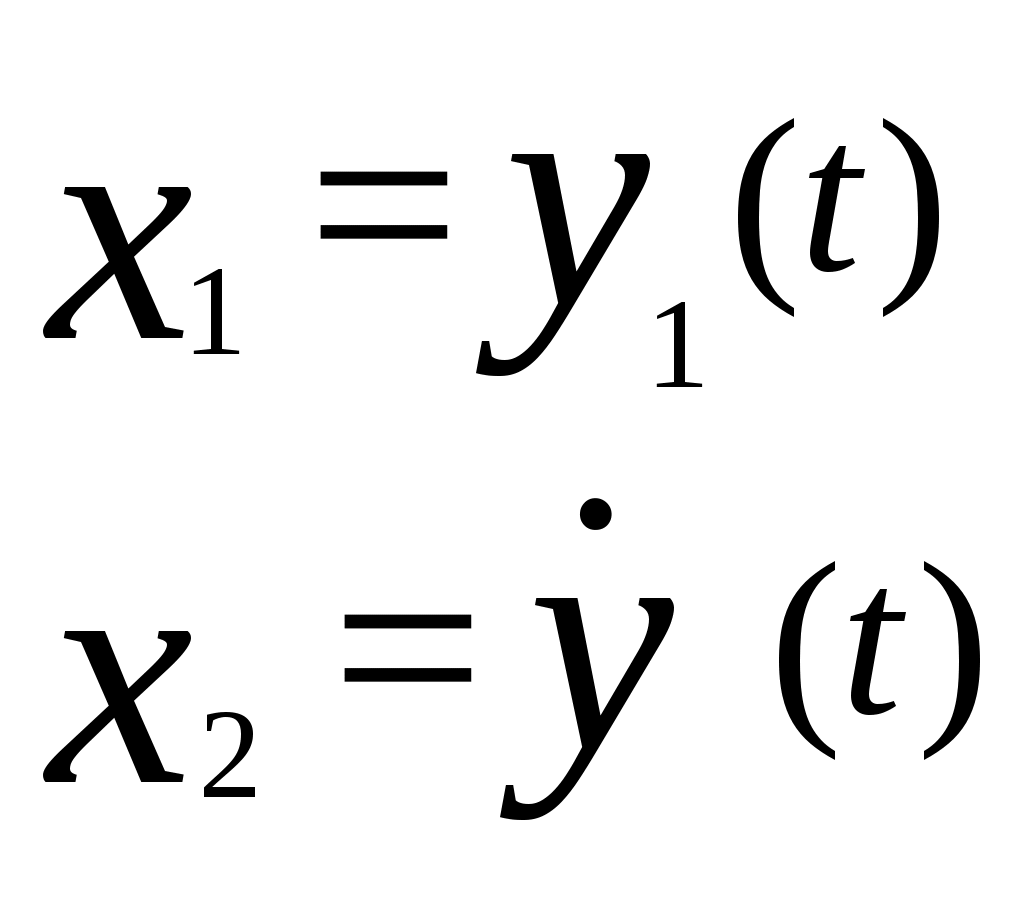
Соответственно соотношение вход-выход-состояние можно записать в виде
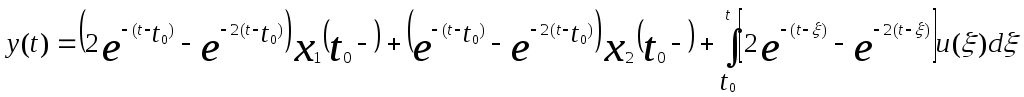, t ≥ t0,а матрицы и векторы будут
,
,
.Список литературы.
Веретенников, В. Н. Обыкновенные дифференциальные уравнения : учебное пособие : [16+] / В. Н. Веретенников. – Москва ; Берлин : Директ-Медиа, 2020. – Ч. 1. – 96 с.
Будак, Б. А. Математика: сборник задач по углублённому курсу : [12+] / Б. А. Будак, Н. Д. Золотарева, Ю. А. Попов ; под ред. М. В. Федотова. – 5-е изд., электрон. – Москва : Лаборатория знаний, 2020. – 329 с.
Абрамян, М. Э. Лекции по дифференциальному исчислению функций одной переменной : учебник : [16+] / М. Э. Абрамян ; Южный федеральный университет. – Ростов-на-Дону ; Таганрог : Южный федеральный университет, 2020. – 228 с.
Осипенко, С. А. Элементы высшей математики : учебное пособие : [16+] / С. А. Осипенко. – Москва ; Берлин : Директ-Медиа, 2020. – 202 с.
Вагин, Д. В. Численное моделирование динамических систем, описываемых обыкновенными дифференциальными уравнениями : учебное пособие : [16+] / Д. В. Вагин ; Новосибирский государственный технический университет. – Новосибирск : Новосибирский государственный технический университет, 2019. – 63 с.