Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ



Группа Ек20ГУ191

Студент

А.Р.Перезолова

МОСКВА 2022

Практическая работа 1

1. Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель



где

- свободный член прямой парной линейной регрессии,

- коэффициент направления прямой парной линейной регрессии,

- случайная погрешность,

N - число элементов генеральной совокупности.

2. В чем суть метода наименьших квадратов?

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 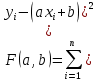принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

---

3. Дайте интерпретацию параметров b1 и b0 линейной модели. Покажите их графическое представление.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение парной регрессии достаточно распространенным в эконометрических исследованиях.

Формально a – значение y при x = 0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a< 0. Интерпретировать можно лишь знак при параметре a. Если a> 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

4. Что оценивает линейный коэффициент корреляции?

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи).

5. Приведите примеры нелинейных моделей по объясняющей переменной x.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

1. полиномы разных степеней

2. равносторонняя гипербола

6. Что понимается под линеаризацией нелинейной модели?

Сущность метода линеаризации заключается в том, что нелинейную функцию заменяют некоторой линейной и затем по уже известным правилам находят числовые характеристики этой линейной функции, считая их приближенно равными числовым характеристикам нелинейной функции.

7. Каким показателем характеризуется теснота связи факторов для нелинейной модели? Каковы свойства этого показателя?

Мерой интенсивности связи при нелинейных соотношениях между переменными служит

---

индекс корреляции.

Индекс корреляции рассчитывается, когда выбрана конкретная нелинейная зависимость между переменными, построена эта зависимость и по ней определены теоретические значения результирующей переменной “ŷ”.

Регрессионный анализ
N=	5
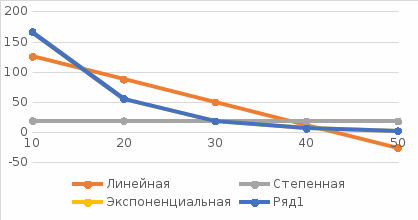
Исходные данные				Линейная		Степенная		Экспоненциальная					лог x(i)		лог y(i)		лог x(i)^2		лог y(i)^2
i	x(i)	y(i)											2,302585		5,114635		4,60517		10,22927
1	10	166,44		125,308		18,9004005		166,5006887					2,995732		4,01476		5,991465		8,02952
2	20	55,41		87,501		18,56350618		55,40494758					3,401197		2,914522		6,802395		5,829044
3	30	18,44		49,694		18,36922632		18,43660973					3,688879		1,814825		7,377759		3,629649
4	40	6,14		11,887		18,23261691		6,134986009					3,912023		0,71295		7,824046		1,4259
5	50	2,04		-25,92		18,12735445		2,041484519			итого		16,30042		14,57169		32,60083		29,14338
Вспомогательные величины
	Сумма x(i)	Сумма y(i)		Сумма x(i)*y(i)		Сумма x(i)^2		Сумма y(i)^2
	150	248,47		3673,4		5500		31154,4365
	Суммлог x(i)	Суммлог y(i)		Суммпрлог x(i)*y(i)		Суммквлог x(i)^2		Суммаx(i)lny(i)			Суммквлог y(i)^2
	16,300417	14,57169174		43,20063948		219,0248369		327,1176971			29,14338347
Параметры		Коэфф.		Линейная		Степенная		Экспоненц.
		В0		-3,7807		20,06404936		500,3610786
		В1		163,115		-0,02594758		-0,110033055

---

Практическая работа 2

1. 
   Назовите основные методы решения ЗЛП.
   

• 
  графический метод
  
• 
  симплексный метод
  
• 
  транспортная задача
  

2. 
   Поясните суть симплекс-метода решения ЗЛП.
   

Симплекс метод - это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).

3. 
   Поясните суть графического решения ЗЛП.
   

Графический метод решения задач ЛП основан на их геометрической интерпретации и применяется для задач, имеющих две переменные. В случае трех переменных графическое решение задачи ЛП становится менее наглядным, а при большем числе переменных вообще невозможным.

5. Какие ресурсные ограничения используются в задачах ЗЛП?

• 
  фонд машинного времени по каждому виду оборудования;
  
• 
  фонд рабочего времени, определяемый численностью персонала;
  
  • 
    фонд материальных ресурсов, которые может получить в планируемый период предприятие от поставщиков по заключенным договорам.
    
  • 
    модели многих задач планирования базируются на законах сохранения (балансовых соотношениях) и эмпирических закономерностях преобразования ресурсов в продукцию (производственных функциях).
    

Математически подобные модели представляются в виде систем m линейных уравнений с n неизвестными, которые решаются с помощью известных методов линейной алгебры (например, методом Гаусса).

Параметры поиска решения

Максимальное время Без пределов, Число итераций Без пределов, Precision 0,000001, Использовать автоматическое масштабирование

Максимальное число подзадач Без пределов, Максимальное число целочисленных решений Без пределов, Целочисленное отклонение 1%, Считать неотрицательными

Ячейка целевой функции (Минимум)

Ячейка

Имя

Исходное значение

Окончательное значение

$D$6

1,2

1,2

Ячейки переменных

Ячейка

Имя

Исходное значение

Окончательное значение

Целочисленное

$A$4

х1

0,6

0,6

Продолжить

$B$4

х2

0

0

Продолжить

Ограничения

Ячейка

Имя

Значение ячейки

Формула

Состояние

Допуск

$D$4

3

$D$4>=$F$4

Привязка

0

$D$5

-2,4

$D$5<=$F$5

Без привязки

11,4

---

Ячейки переменных
			Окончательное	Приведенн.	Целевая функция	Допустимое	Допустимое
	Ячейка	Имя	Значение	Стоимость	Коэффициент	Увеличение	Уменьшение
	$A$4	х1	0,6	0	2	5,5	2
	$B$4	х2	0	2,2	3	1E+30	2,2
Ограничения
			Окончательное	Тень	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	Значение	Цена	Правая сторона	Увеличение	Уменьшение
	$D$4		3	0,4	3	1E+30	3
	$D$5		-2,4	0	9	1E+30	11,4

---

Смотрите также файлы

• Лабораторная работа 1 по учебному курсу Физика 3.docx

• 1 Счета бухгалтерского учета и двойная запись.pdf

• Соблюдаем пунктуационные нормы Задание Расставьте знаки препинания в сложноподчиненных предложениях из комедии А. П. Чехова Вишневый сад.docx

• Военная тематика в лирике Б. Окуджавы (по выбору преподавателя) Творческая работа.docx

• 1. Требования морского регистра судоходства.docx