Рис. 1.4. Переходная характеристика двигателя по моменту сопротивления

Установившиеся значения скорости вращения двигателя при наличии управляющего воздействия и момента сопротивления составляют, соответственно,

рад/с и рад/с.

Определим относительную погрешность по формуле

.

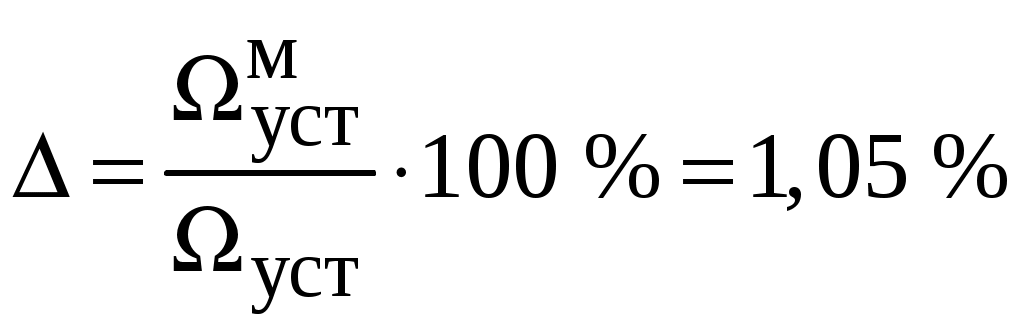Наличие моментной составляющей погрешности говорит о том, что механическая характеристика двигателя не является абсолютно жесткой. Для устранения моментной составляющей погрешности в контуре скорости рассчитывается регулятор скорости, обеспечивающий настройку на оптимум по модулю, и искусственная механическая характеристика контура скорости становится абсолютно жесткой.

2. ОПТИМИЗАЦИЯ КОНТУРА СКОРОСТИ
2.1. Синтез регулятора скорости
Начальные данные:

- постоянная времени БП Т_бп = 0,003 с;

- постоянная времени ТГ Т_тг = 0,007 с;

- момент сопротивления нагрузки = 165 Нм;

- входное напряжение суммирующего усилителя КС = 10 В;

- выходное напряжение усилителя регулятора скорости = 2 В. 1. Коэффициент передачи тахогенератора

К_тг = ;

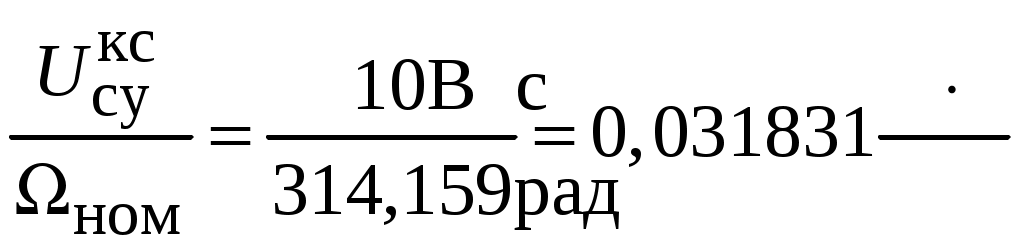коэффициент передачи блока питания

;

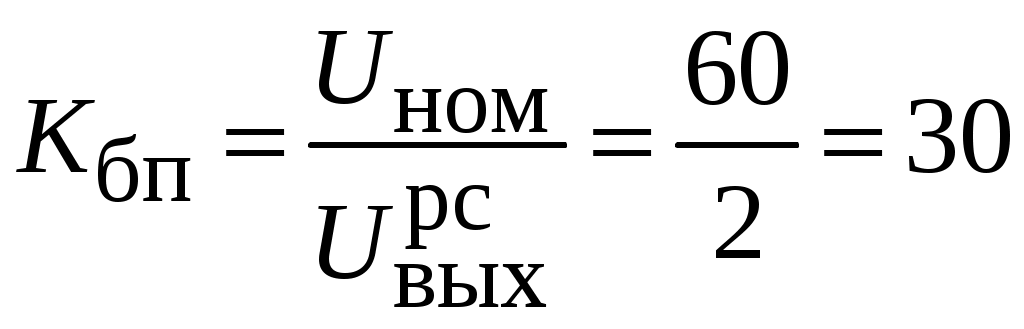постоянные времени РС

с;

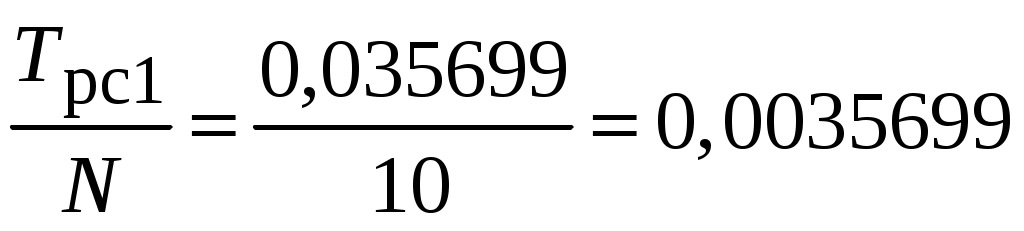с;

с.

Задаём Т_рс3 = 0,002 с.

Суммарная малая постоянная времени контура скорости

---

с.

Для моделирования строим ССДМ КС по схеме на рис. 2.1.




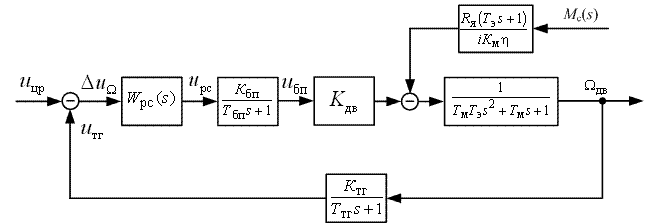
Рис. 2.1. Структурная схема динамической модели контура скорости
2. Реализацию динамического звена на входе воздействия момента сопротивления нагрузки (рис. 2.2) необходимо выполнить с добавлением удалённого полюса с малой постоянной времени с. ССДМ КС в системе Simulink представлена на рис.2.2.

Коэффициент передачи двигателя по скорости.


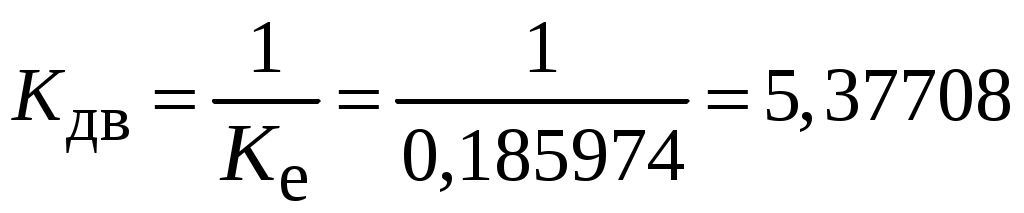
Передаточная функция регулятора скорости


.


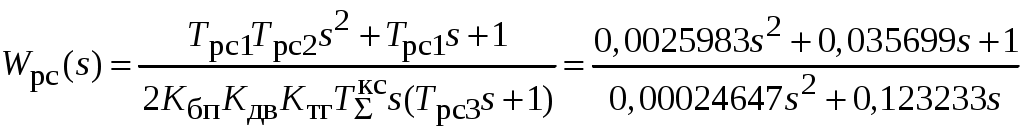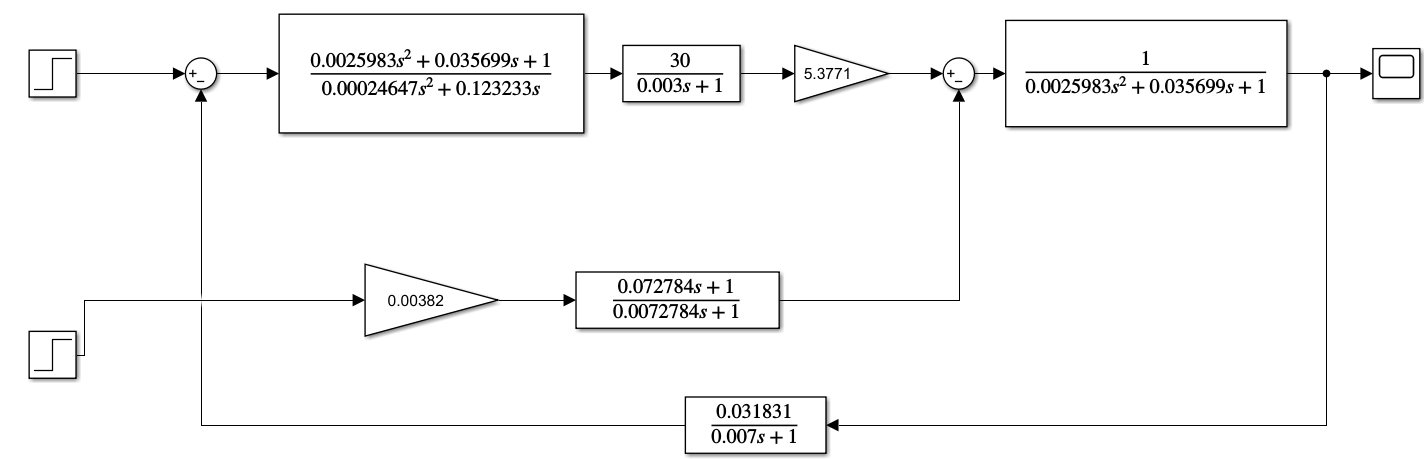
Рис. 2.2. Структурная схема динамической модели контура скорости

в системе Simulink
Для построения переходной характеристики по управляющему воздействию необходимо нажать пиктограмму Start Simulation. Перед этим устанавливается время интегрирования, в 6 ÷ 10 раз превышающее максимальную постоянную времени контура скорости (в меню Simulation Parameters на вкладке Solver устанавливается время интегрирования Stop Time).

Для моделирования в блоке Step задаём входное воздействие В, а в блоке Step 1 значение момента сопротивления нагрузки . На рис. 2.3 изображена соответствующая переходная характеристика контура скорости по управляющему воздействию.

Для построения переходной характеристики по моменту сопротивления нагрузки М_с устанавливаем соответственно в блоке Step входное воздействие , а в блоке Step 1 – момент сопротивления .

3. Переходим к анализу полученных графиков. По графику на рис. 2.3 определяем максимальное значение угловой скорости вращения двигателя Ω_max = 331,522 рад/с и установившееся значение скорости Ω_уст = 314,176 рад/с. По этим данным рассчитываем перерегулирование

---

.

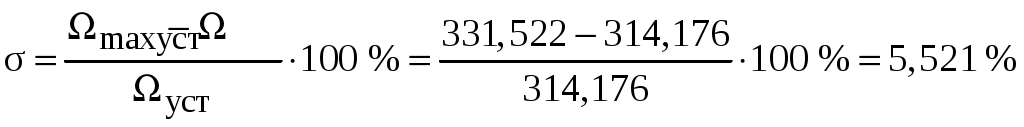Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Т_тг. Если принять Т_тг = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном

W_тг(s) = К_тг.

Ω(t), рад/с

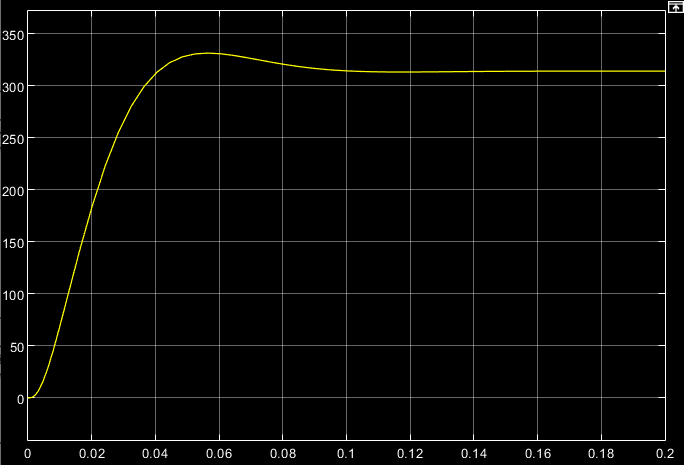t, c
Рис. 2.3. Переходная характеристика контура скорости по управляющему воздействию
Ω(t), рад/с

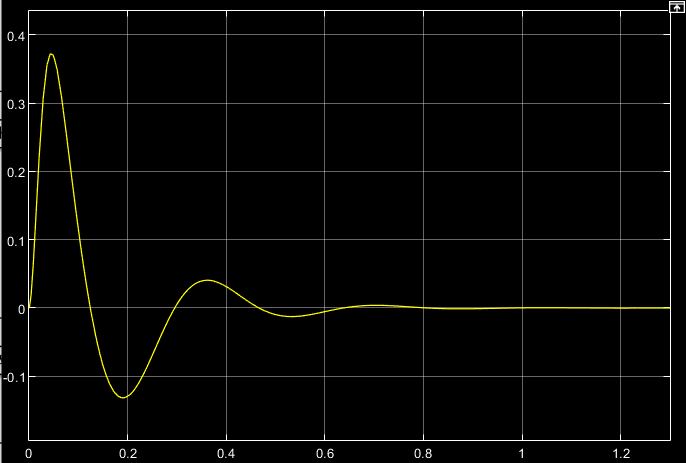t, c
Рис. 2.4. Переходная характеристика контура скорости по моменту

сопротивления

При этом суммарную малую постоянную времени КС следует рассчитывать по формуле

.

Время нарастания определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ω_уст и составляет

0,04112 с.

Проверяем соответствие полученного значения требованиям настройки на ОМ

с.

Из анализа графика на рис. 2.4 следует, что при воздействии неизменного по величине момента сопротивления М_с моментная составляющая ошибки ΔΩ_м примерно через 0,8 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жёсткой. Увеличение точности обусловлено наличием в структуре регулятора скорости интегральной составляющей.

4. Для построения ЛЧХ необходимо написать программу в Command Window системы MatLab. Поскольку ЛЧХ строятся на основе передаточной функции разомкнутого контура скорости, то все передаточные функции соответствующих элементов, входящих в него, необходимо перемножить и получить

.

Обозначая W_рс(s) = sys1, W_бп(s) = sys2, W_дв(s) = sys3, W_тг(s) = sys4, составляем программу в соответствии со следующим алгоритмом:

num1 = [0.0025983 0.035699 1];

---

den1 = [0.00024647 0.123233 0];

sys1 = tf(num1, den1);

num2 = [30];

den2 = [0.003 1];

sys2 = tf(num2, den2);

num3 = [5.3771];

den3 = [0.0025983 0.035699 1];

sys3 = tf(num3, den3);

num4 = [0.031831];

den4 = [0.007 1];

sys4 = tf(num4, den4);

sys5 = sys1*sys2*sys3*sys4
Transfer Function:


0.01334 s^2 + 0.1833 s + 5.135

--------------------------------------------------------------------------------------

1.345e-11 s^6 + 1.331e-08 s^5 + 4.028e-06 s^4 + 0.000378 s^3 + 0.005878 s^2 + 0.1232 s

В результате решения будет получена искомая передаточная функция разомкнутого КС с численными значениями коэффициентов полиномов числителя и знаменателя b₂, b₁, b₀, d₆, d₅, d₄, d₃, d₂, d₁, d₀ = 0
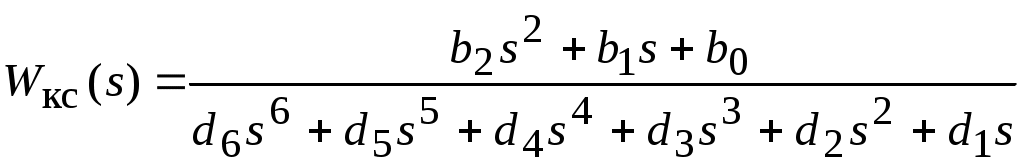(2.1)

Далее переходим к построению ЛЧХ:

w = logspace(-3, 3);

num = [0.01334 0.1833 5.135];

den = [1.345e-11 1.331e-08 4.028e-06 0.000378 0.005878 0.1232 0];

bode(num, den, w)


Результаты моделирования представлены на рис. 2.5.
Значения (– n, m) являются показателями степени при основании 10, указывающие диапазон частот. Обычно ограничиваются диапазоном – 3, 3. В этом случае частота будет изменяться в пределах .

Из анализа графиков видно, что запасы устойчивости по фазе и амплитуде составляют L_з = 16,2 дБ (Gain Margin) и (Phase Margin) соответственно.

Запас устойчивости по амплитуде L_з определяется как разность между линией 0 дБ и значением логарифмической амплитудно-частотной характеристики (ЛАЧХ) на частоте, соответствующей точке пересечения графика фазовой частотной характеристики со значением – 180°.

Запас устойчивости по фазе вычисляется по формуле

.

Значение фазы соответствует частоте среза ω_с, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ.


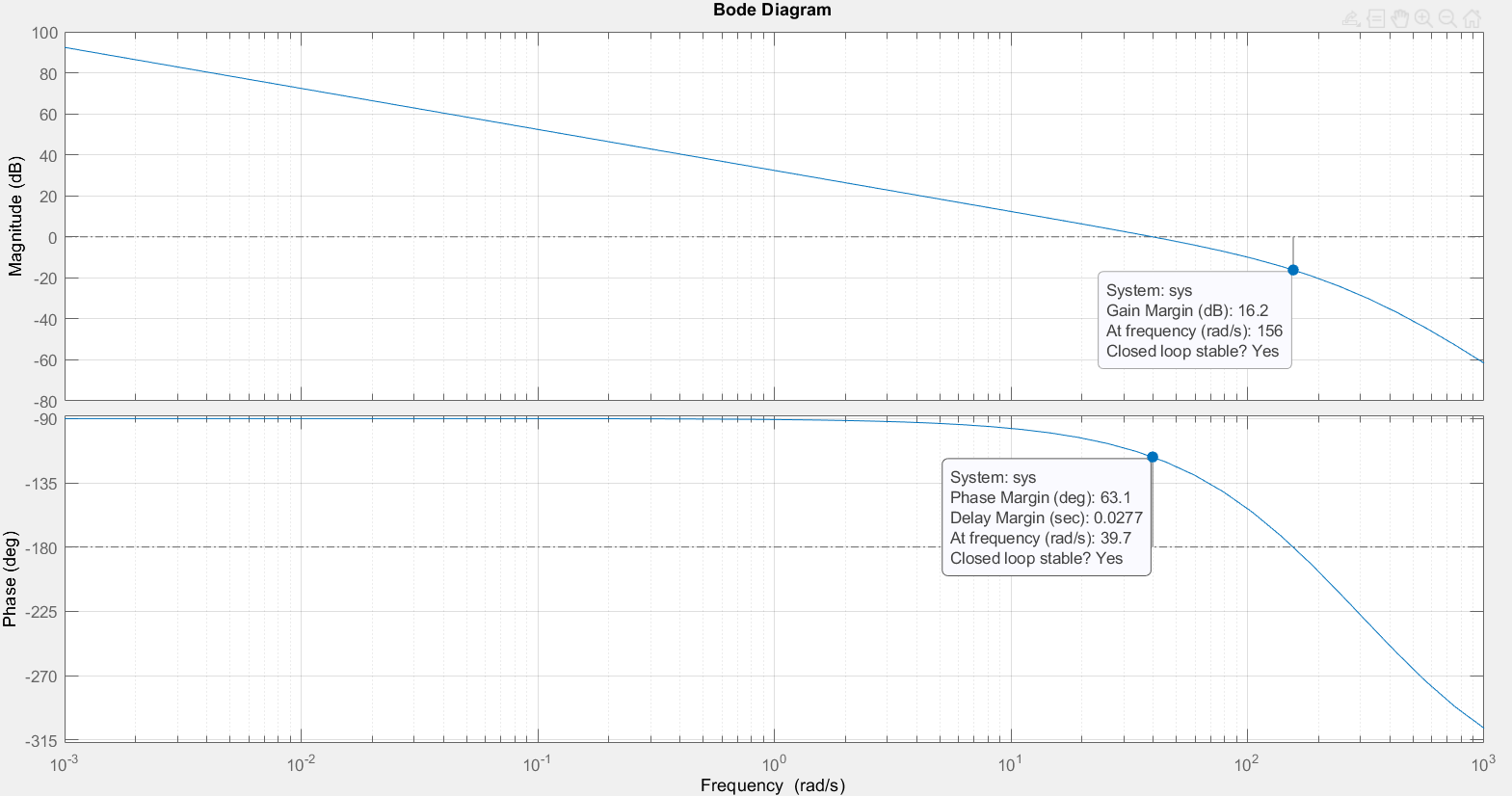
Рис. 2.5. Логарифмические частотные характеристики контура скорости
Результаты моделирования подтверждают правильность расчёта параметров РС и позволяют сделать вывод о том, что КС настроен на ОМ.

3. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ЦИФРОВОГО РЕГУЛЯТОРА СКОРОСТИ И МОДЕЛИРОВАНИЕ КОНТУРА СКОРОСТИ

---

3.1. Программная реализация регулятора скорости и моделирование контура скорости
Начальные данные:
-период квантования Т₀ = 0,001 с.
Преобразуем передаточную функцию регулятора скорости

,

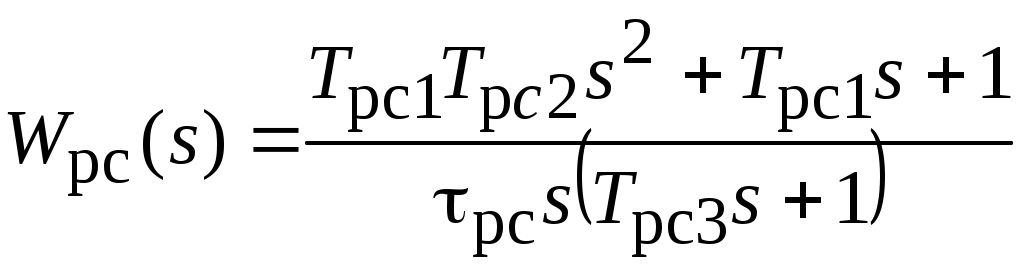к виду

.

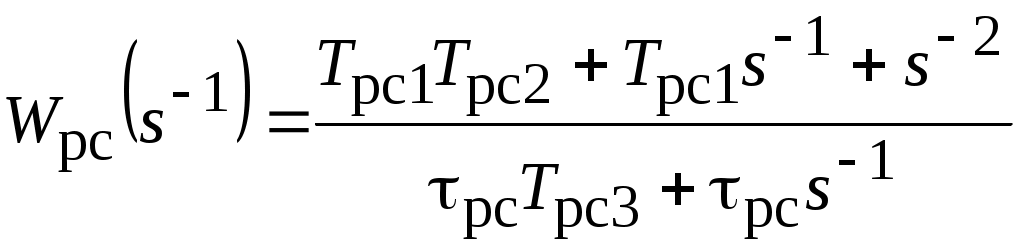Параметр с

1. 
   С помощью формулы трапеций определим
   

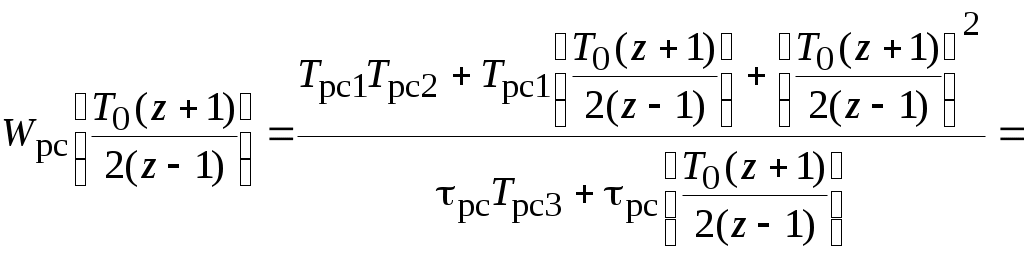
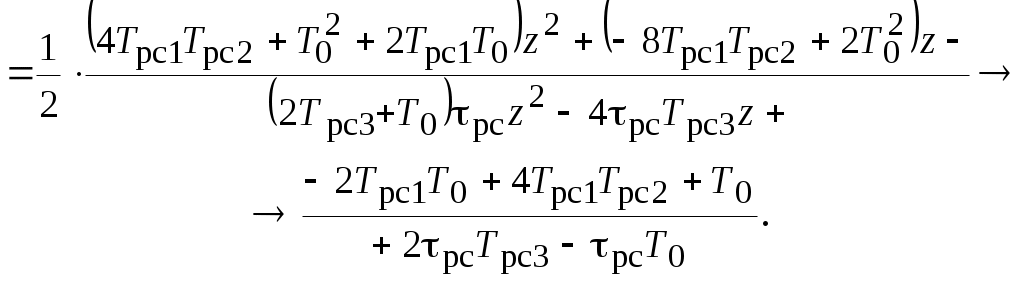
Тогда

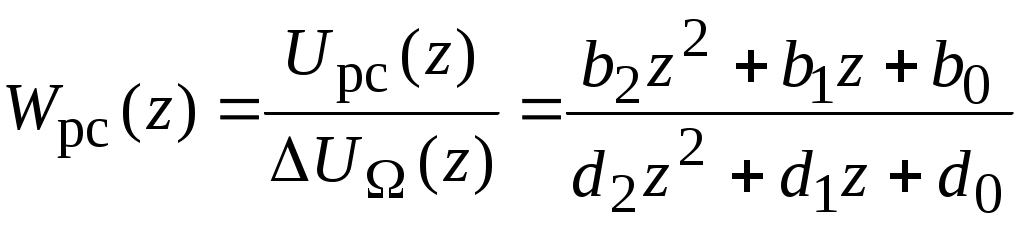. (3.1)

Заметим, что переход к z-преобразованию с применением MatLab предусматривает деление на коэффициент при старшей степени z в знаменателе. В нашем случае коэффициент при z²

.

Тогда в выражении (3.1)

; ; ;

; ; .

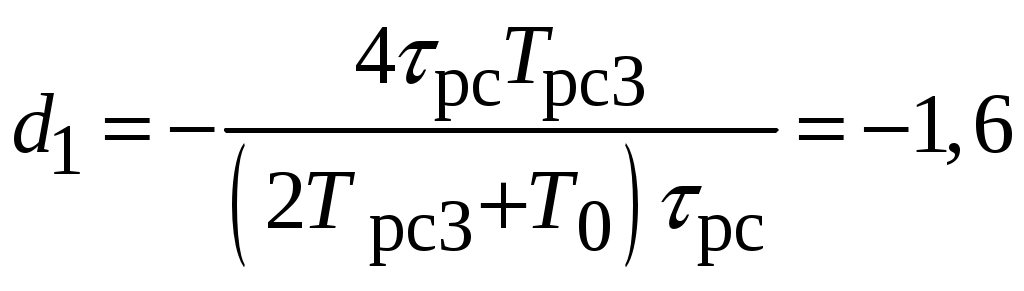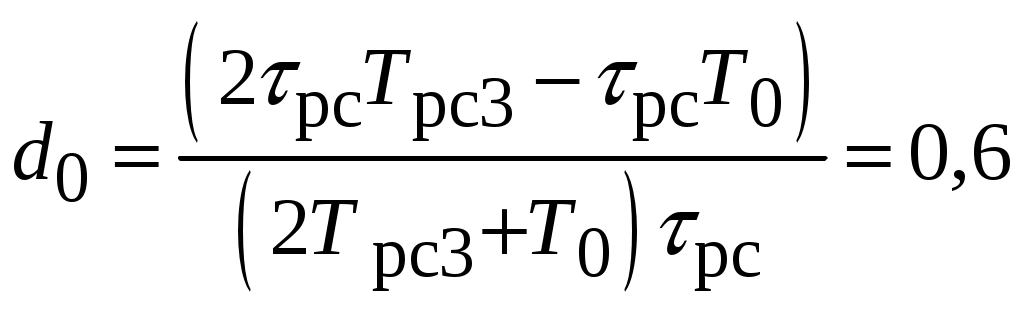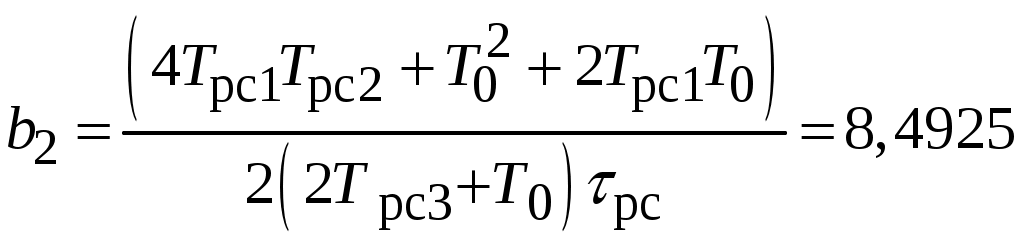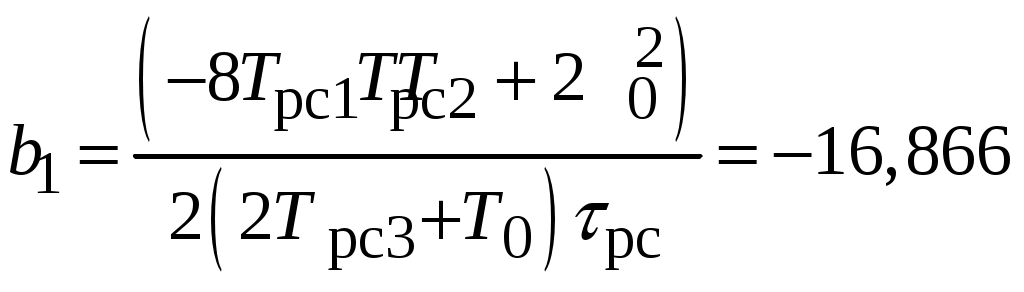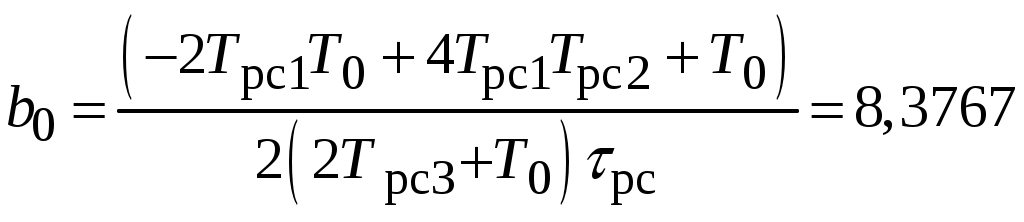Здесь = 0,12323 с; Т_рс1 = 0,035699 с; Т_рс2 = 0,072784 с; Т_рс3 = 0,002 с.

2. 
   Составляем структурную схему программирования.
   

По уравнениям состояния и выхода определяем коэффициенты матриц А, B, C, D соответственно

; ; ; .

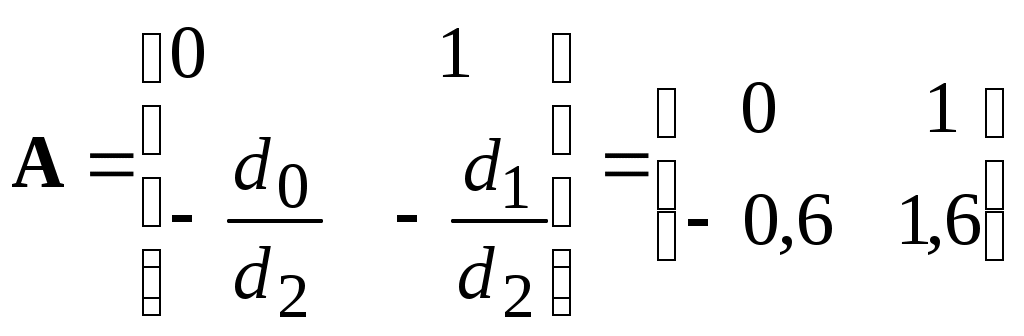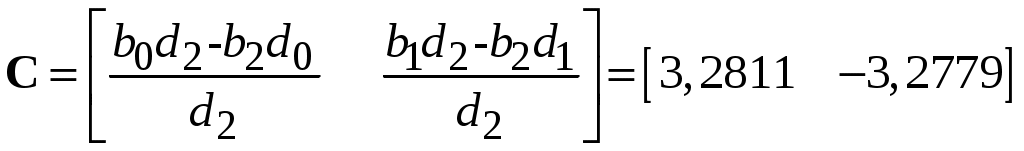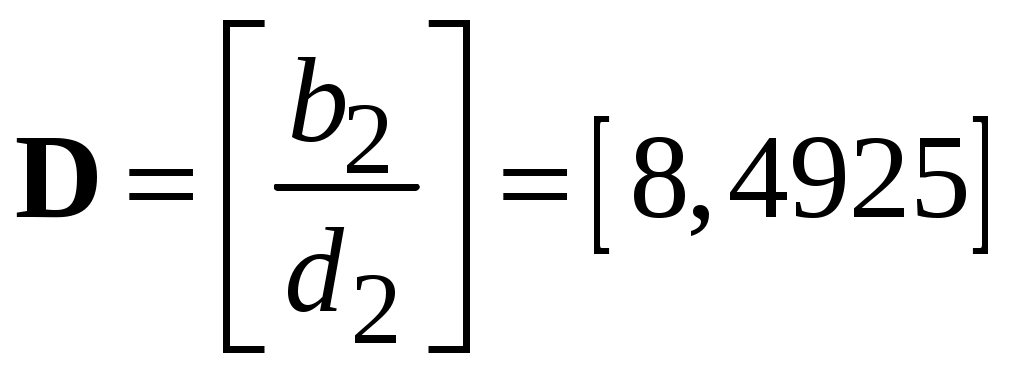3.2. Реализация ССДМ КС с цифровым регулятором скорости и получение переходных характеристик по управляющему и возмущающему воздействиям.

---

Смотрите также файлы

• Практическая работа 6 и 7 уравнение состояния идеального газа и Изопроцессы на графике.docx

• Отчет о прохождении производственной практики Летняя практика в доо (по профилю специальности).docx

• Базы данных и средства управления базами данных.docx

• Решение Начислена арендная плата за пользование помещением10000 Дт 0 109 Х0 224 Кт 0 302 24 730.doc

• Функции, структура, классификация.doc