Параметры двигателя, БП, ТГ и цифрового регулятора принять из пунктов 1.1, 2.1, 3.1. Коэффициент передачи АЦП К_vz2 = 1.

1. Для моделирования построим ССДМ КС с цифровым регулятором скорости в системе Simulink (рис. 3.1).


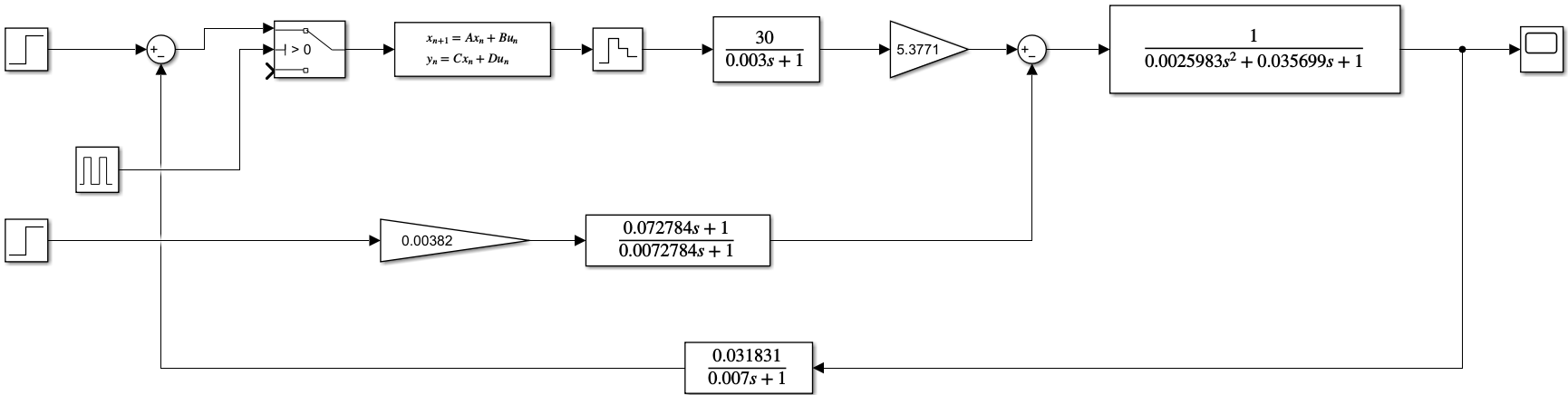
Рис. 3.1. Структурная схема динамической модели контура скорости

с цифровым регулятором скорости
Цифровой регулятор скорости реализован блоком Discrete State-Space, расположенным в библиотеке блоков Discrete. Диалоговое окно блока представлено на рис. 3.2.



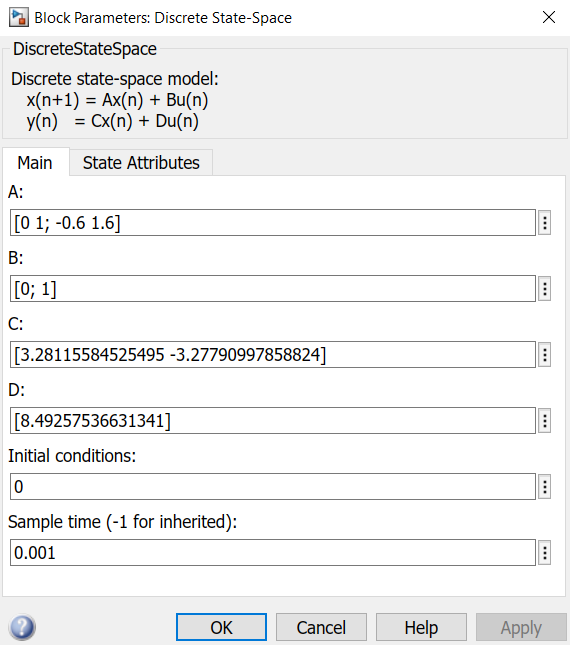
Рис. 3.2. Диалоговое окно блока Discrete State-Space
Блок Zero-Order Hold представляет собой экстраполятор нулевого порядка, восстанавливающий непрерывный сигнал u_рс с выхода цифрового регулятора скорости. Блок Switch реализует модель квантователя, преобразующего непрерывный сигнал рассогласования∆u_Ω в дискретный. Блок Pulse Generator формирует последовательность единичных импульсов с периодом следования Т₀.

Для задания параметров блока Zero-Order Hold необходимо в строке Sample time установить период квантования Т₀ (рис. 3.3).



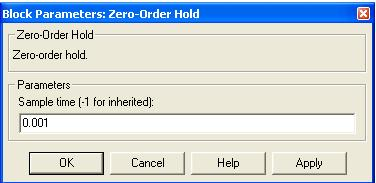
Рис. 3.3. Диалоговое окно блока Zero-Order Hold
Для задания параметров блока Pulse Generator необходимо в строке Period установить период квантования Т₀ (рис. 3.4).



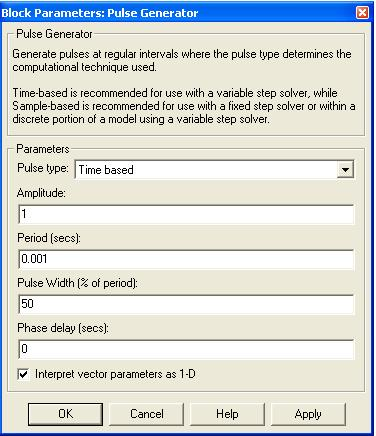
Рис. 3.4. Диалоговое окно блока Pulse Generator
2. Для получения графика в блоке Step задаём входное воздействие В, а в блоке Step1 значение момента сопротивления . На рис. 3.5 изображена переходная характеристика контура скорости по управляющему воздействию. Время моделирования составляет 0,5 с.
Ω(t), рад/с

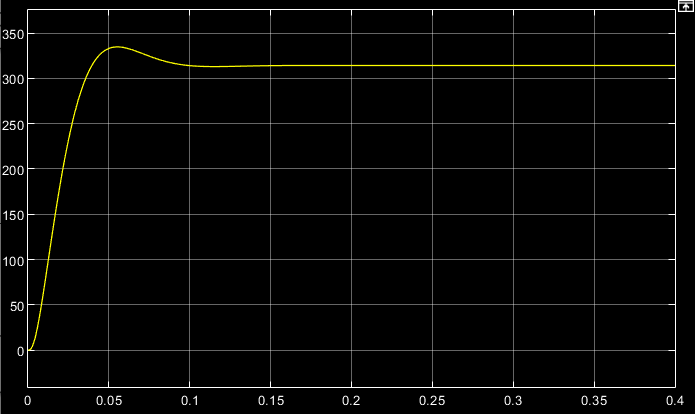
t, c
Рис. 3.5. Переходная характеристика контура скорости по управляющему воздействию
Ω(t), рад/с

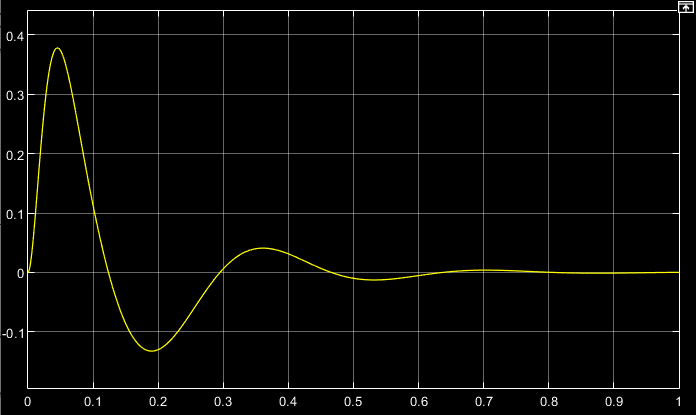
t, c
Рис.3.6. Переходная характеристика контура скорости по моменту

сопротивления
Для построения переходной характеристики по моменту сопротивления нагрузки

---

устанавливаем в блоке Step входное воздействие , а в блоке Step 1 момент сопротивления . Результаты моделирования представлены на рис. 3.6.

3. 
   Переходим к анализу полученных графиков. По характеристике на рис. 3.5 определяем максимальное значение угловой скорости вращения ЭД Ω_max = 334,74 рад/с и установившееся значение Ω_уст = 314,158 рад/с. По этим данным рассчитываем перерегулирование
   

.

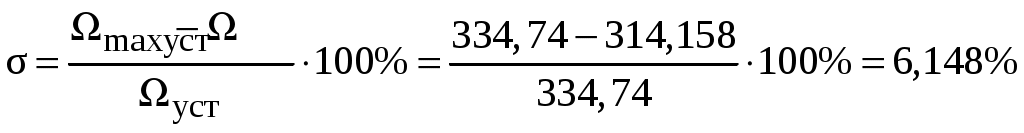Время нарастания составляет

0,0395 с.

Проверяем соответствия требованиям настройки на ОМ

с.

Анализ полученных результатов показывает, что дискретная аппроксимация регулятора скорости привела к уменьшению запасов устойчивости, поэтому перерегулирование σ увеличилось, а время нарастания уменьшилось по сравнению с аналоговой моделью регулятора скорости.

3.3. Построение графика ЛЧХ разомкнутого КС. Анализ результатов моделирования.

Для расчетов принять период квантования Т₀ = 0,002 с.

Для построения частотных характеристик к выражению (2.1) применим z-преобразование в соответствии с формулой трапеций. Числовые значения коэффициентов разомкнутого контура скорости получены в пункте 2.1 (программа построения ЛЧХ).

Программа для перехода переменной zзаписывается в Command Window следующим образом:
num = [0.01334 0.1833 5.135];

den = [1.345e-11 1.331e-08 4.028e-06 0.000378 0.005878 0.1232 0];

Fs=500;

[numd,dend] = bilinear(num,den,Fs)

Результат:

numd =

0.000434 0.00088 -0.000396 -0.0017 -0.000455 0.000833 0.000422

dend =

1.0000 -4.5547 8.4406 -8.112 4.2427 -1.1382 0.12161

В приведённой программе частота дискретизации

---

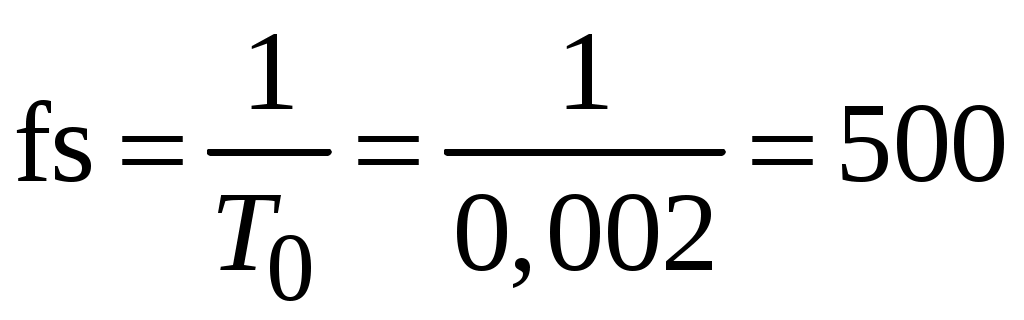
Гц.

Полученные численные значения позволяют записать передаточную функцию разомкнутого контура скорости относительно переменной z:

,

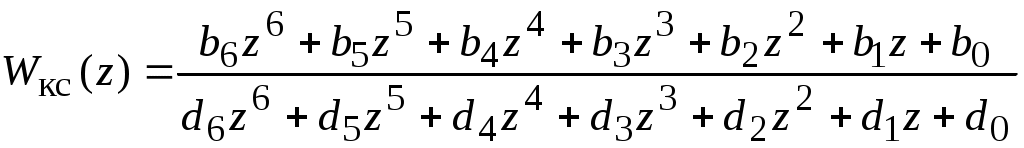где b₆= 0.000434;b₅= 0.00088; b₄= -0.000396; b₃= -0.0017; b₂= -0.000455; b₁= 0.000833; b₀= 0.000422;

d₆= 1,0; d₅= -4.5547; d₄= 8.4406; d₃= -8.112;d₂= 4.2427; d₁= -1.1382; d₀= 0.12161.

К полученному выражению применим -преобразование

.



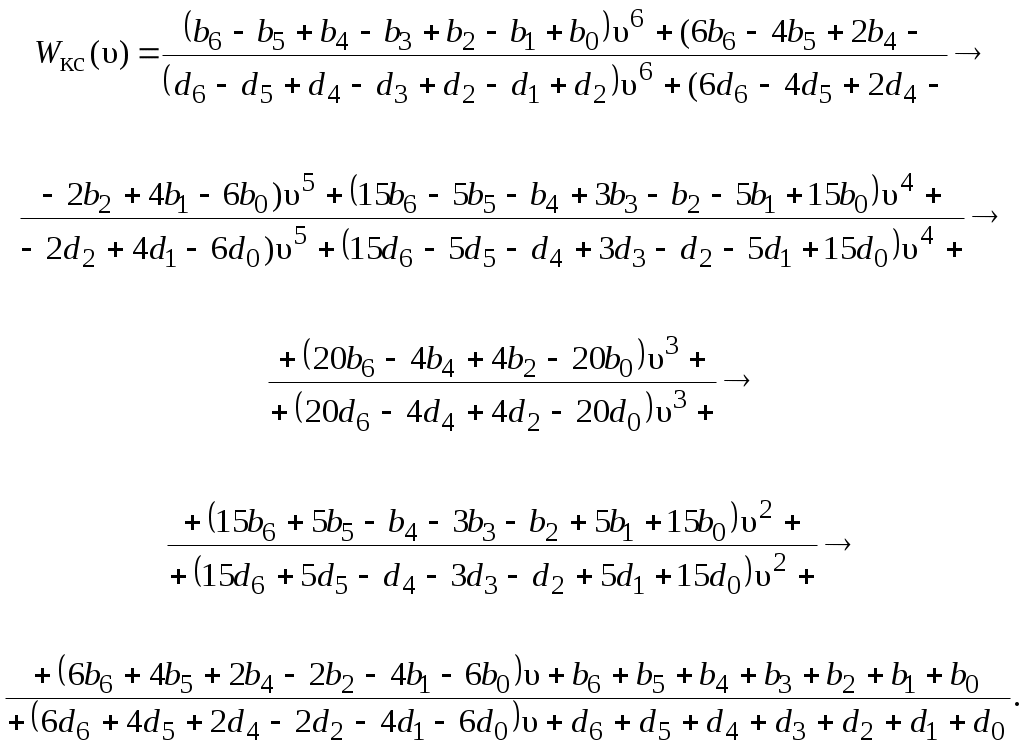
После вычисления коэффициентов при переменной υ и приведения к стандартному виду, получим

.

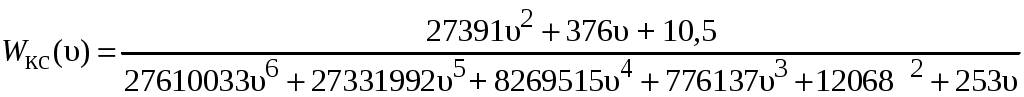Далее переходим к построению логарифмических псевдочастотных характеристик (ЛПЧХ) в соответствии с программой:

w = logspace(-3, 3);

num = [0 0 0 0 27391 376 10.5];

den = [ 253 0];

bode(num, den, w)

Результаты моделирования представлены на рис. 3.7.

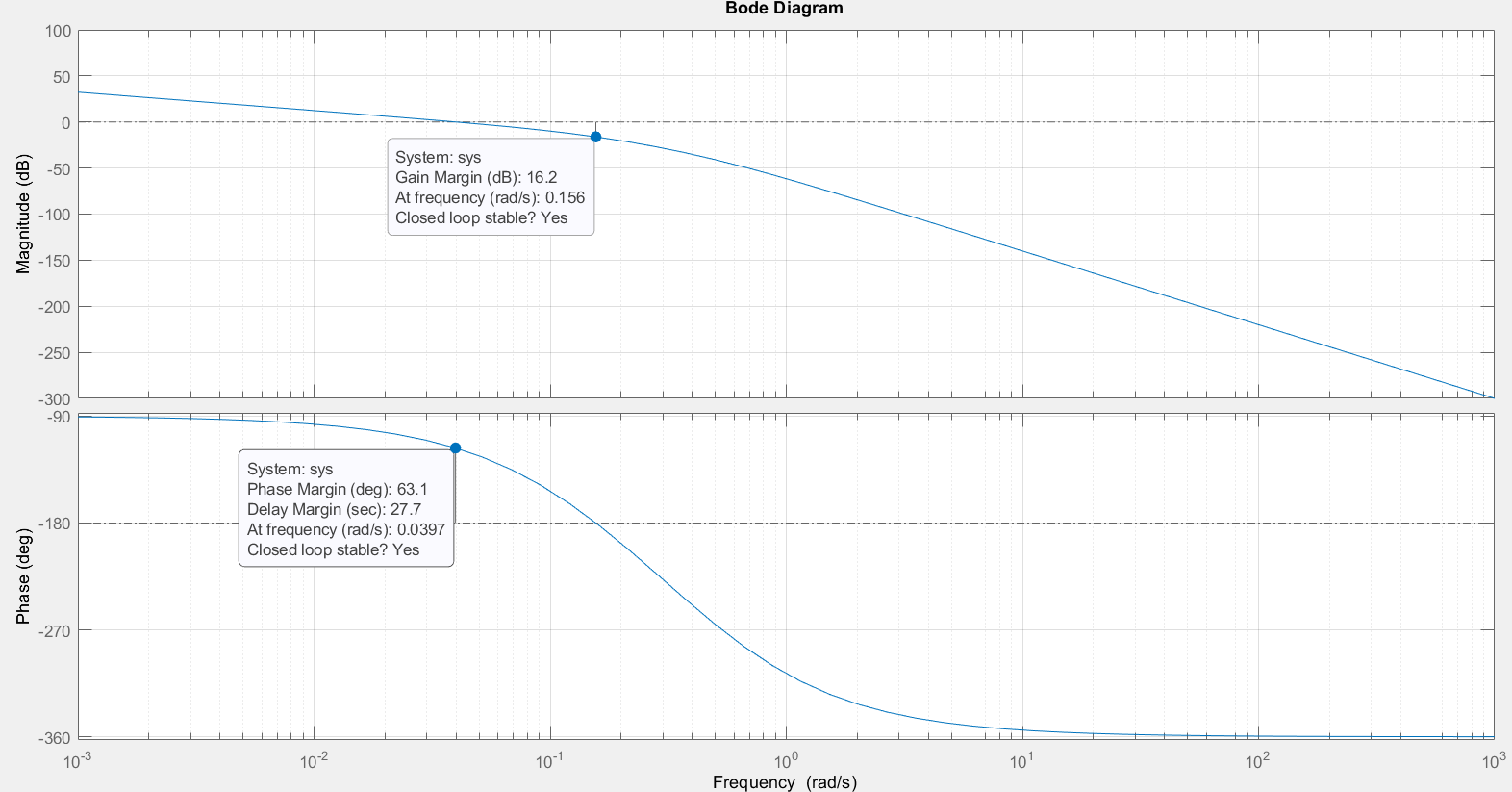
Рис. 3.7. Логарифмические псевдочастотные характеристики

контура скорости
При увеличении перерегулирования (см. пункт 3.2) запасы устойчивости по фазе и амплитуде не изменились по сравнению с аналоговым контуром скорости. Так, запас устойчивости по фазе на псевдочастоте среза равен

,

а запас устойчивости по амплитуде на псевдочастоте равен

дБ.

При переходе к абсолютной псевдочастоте среза

---

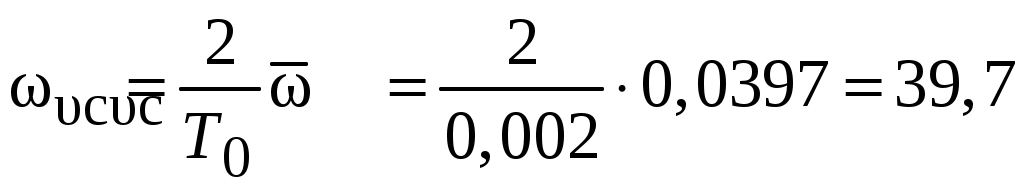с^{– 1},

а частота

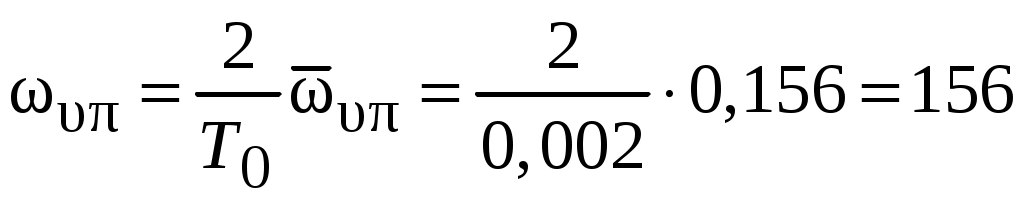с^{– 1}.

Графики ЛПЧХ сдвигаются вправо относительно оси частот на величину , при этом запасы устойчивости по фазе и амплитуде останутся прежними.

4.СИНТЕЗ РЕГУЛЯТОРА ПОЛОЖЕНИЯ
4.1. Синтез регулятора положения в системе с астатизмом первого порядка
Синтезируем регулятор положения с применением ЛЧХ на основе критерия динамической точности системы. Для расчётов примем следующие параметры:

- максимальная угловая скорость нагрузки Ώ_max = 33 град/с;

- максимальное угловое ускорение нагрузки ε_max = 22 град/с²;

- ошибка по скорости _ = 10 мин;

- ошибка по ускорению _ = 35 мин.

Моментную составляющую ошибки определяем при отработке квадратично возрастающего момента сопротивления 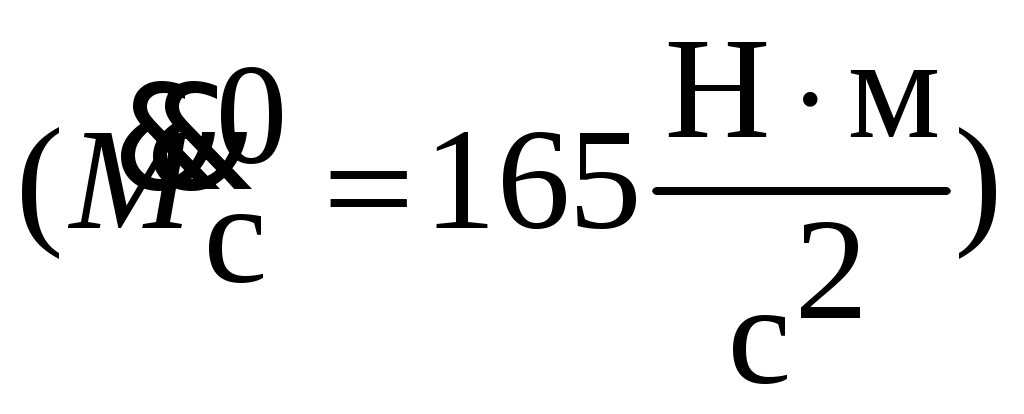. Определяем параметры желаемой передаточной функции ЭП (4.8).

Коэффициент передачи по скорости

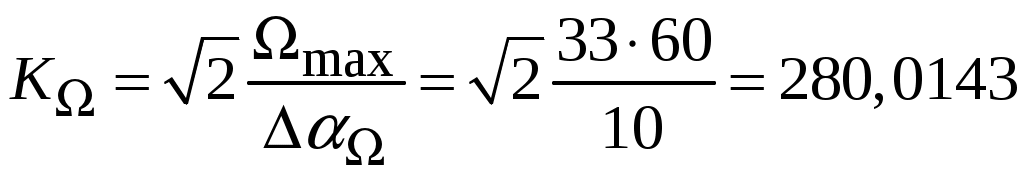с^{– 1}.

Коэффициент передачи по ускорению

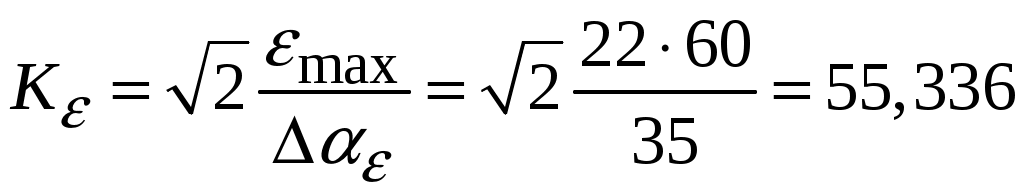с^{– 2}.

Значение базовой частоты будет равно

с^{– 1}.

По выражениям (4.8) рассчитываем постоянные времени

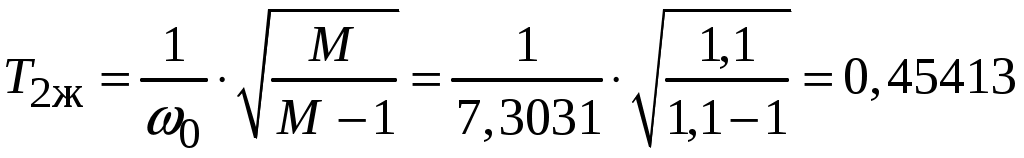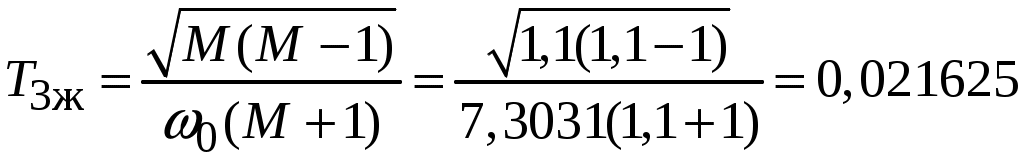с;

с.

Рассчитываем протяжённость среднечастотного участка желаемой ЛАХ

.

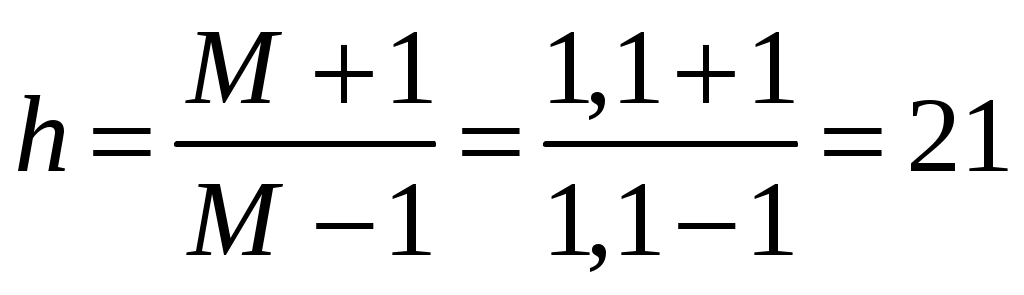Частоту, соответствующую максимальному запасу по фазе определяем по формуле

---

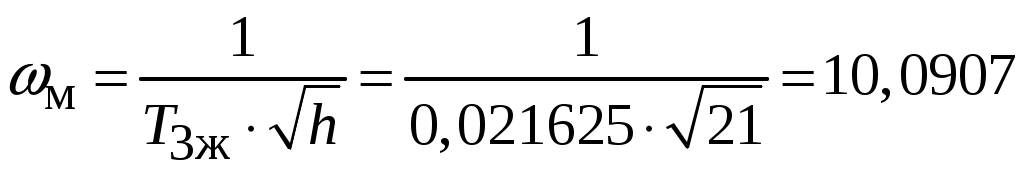с^{– 1}.

По условию обеспечения максимального запаса по фазе находим постоянную времени

 1/ = 1/10,0907 = 0,991 с.

Принимаем = 2 с.

С учётом проведённых расчётов желаемая передаточная функция ЭП с астатизмом первого порядка запишется как

.

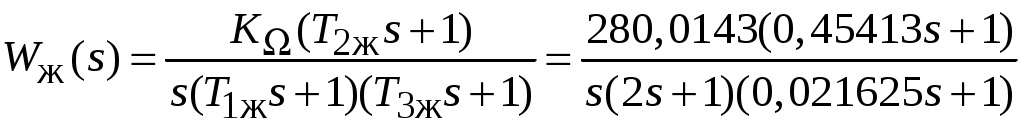2. Для построения ССДМ неизменяемой части ЭП запишем исходные данные тахогенератора и параметры контура скорости:

- коэффициент передачи тахогенератора К_тг = 0,031831 В·с/рад;

- постоянная времени тахогенератора Т_тг = 0,007 с;

- суммарная малая постоянная времени КС

с;

- коэффициент передачи датчика положения К_дп = 38 рад/В;

- передаточное число редуктора i = 404.

Передаточная функция замкнутого контура скорости

.

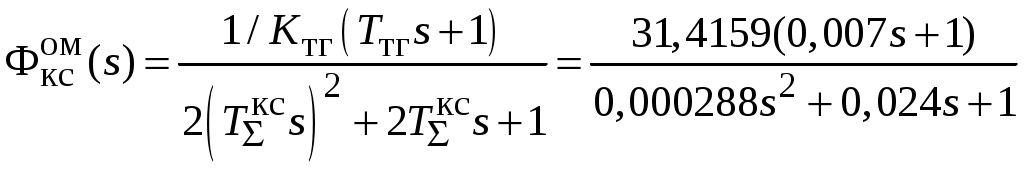3. Составляем программу 1 в среде MatLab для определения передаточной функции регулятора положения ЭП с астатизмом первого порядка.
Программа 1

num1=[127.1645 280.01428];

den1=[0.043251 2.02162 1 0];

sys1=tf(num1, den1);

num2=[8.35663 1193.805];

den2=[0.116352 9.696 404 0];

sys2=tf(num2, den2);

sys=sys1/sys2

Transfer function:

14.8 s^4 + 1266 s^3 + 5.409e04 s^2 + 1.131e05 s

-----------------------------------------------

0.3614 s^4 + 68.53 s^3 + 2422 s^2 + 1194 s

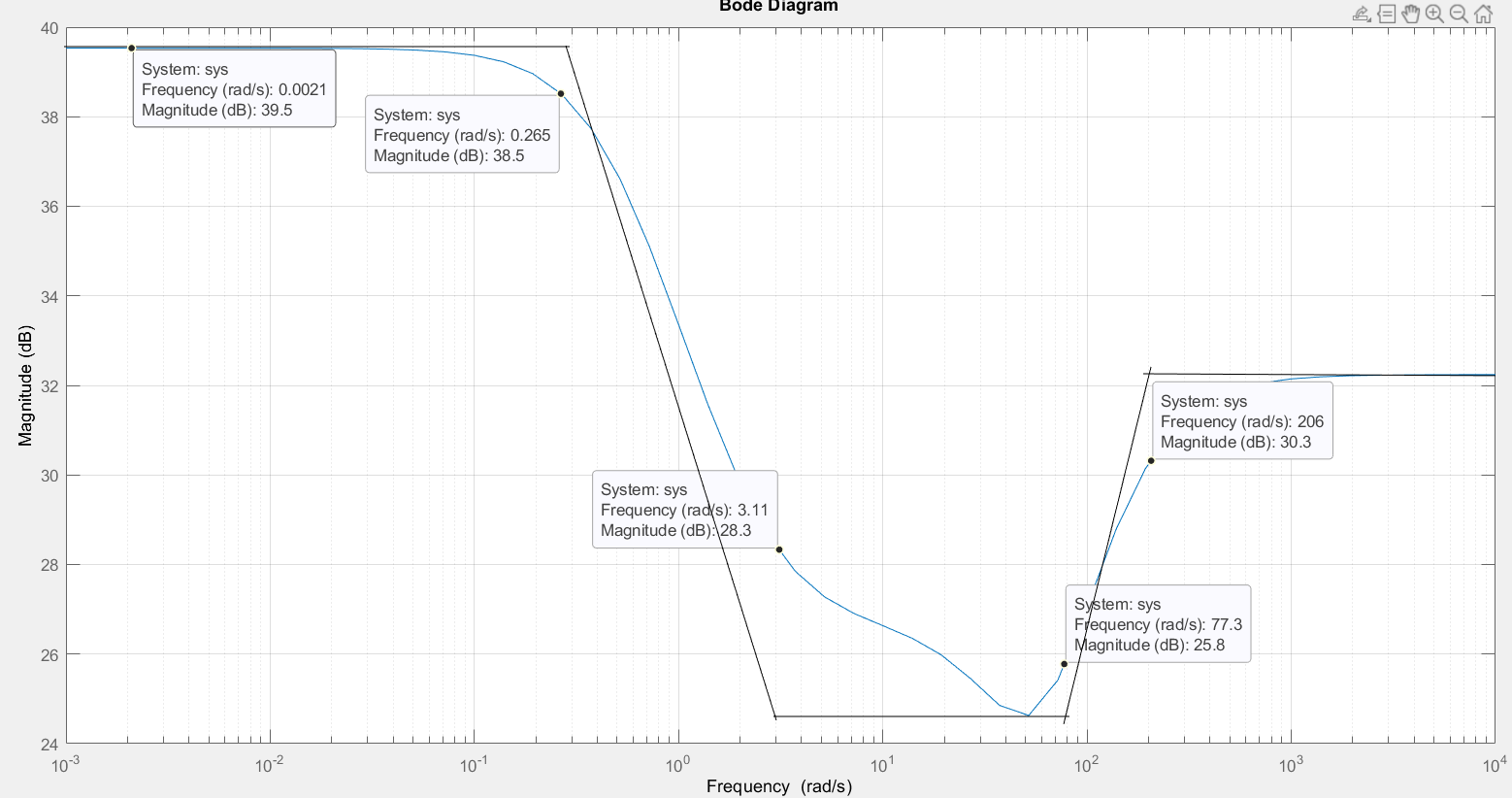
4. Составляем программу 2 в среде MatLab для определения ЛАЧХ регулятора положения, представленную на рис. 4.1.

Программа 2

w=logspace(-3, 4);

num=[14.8 1266 5.409e04 1.131e05 0];

den=[0.3614 68.53 2422 1194 0];

bode(num, den, w)

Переходим к анализу полученных графиков. Низкочастотный участок ЛАЧХ РП проходит параллельно оси частот, постепенно изменяя наклон к среднечастотному участку в пределах от 0 до –20 дБ/дек и далее к 0 дБ/дек. Высокочастотный участок ЛАЧХ с увеличением частоты изменяет свой наклон также в пределах от 20 до 0 дБ/дек. Полученные ЛАЧХ следует аппроксимировать пятью асимптотами и придать регулятору положения свойства интегро-дифференцирующего регулятора.

---

Смотрите также файлы

• Практическая работа 6 и 7 уравнение состояния идеального газа и Изопроцессы на графике.docx

• Отчет о прохождении производственной практики Летняя практика в доо (по профилю специальности).docx

• Базы данных и средства управления базами данных.docx

• Решение Начислена арендная плата за пользование помещением10000 Дт 0 109 Х0 224 Кт 0 302 24 730.doc

• Функции, структура, классификация.doc