Файл: Курсовая работа по дисциплине Цифровые системы управления в мехатронике.doc
Добавлен: 22.11.2023
Просмотров: 132
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 4.1. ЛАЧХ регулятора положения
Рассчитаем параметры передаточной функции.
Находим коэффициент передачи Крп. Из графика рис. 4.1 имеем
дБ,откуда
= 94,406. Частоты сопряжения 1 = 0,265 с– 1; 2 = 3,11 с– 1; 3 = 77,3 с– 1; 4 = 206 с– 1 и постоянные времени
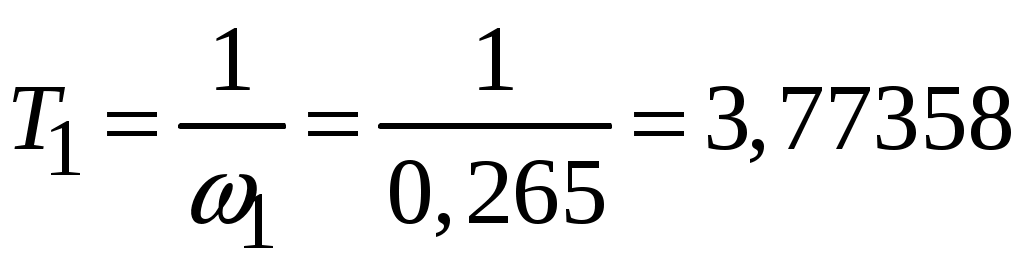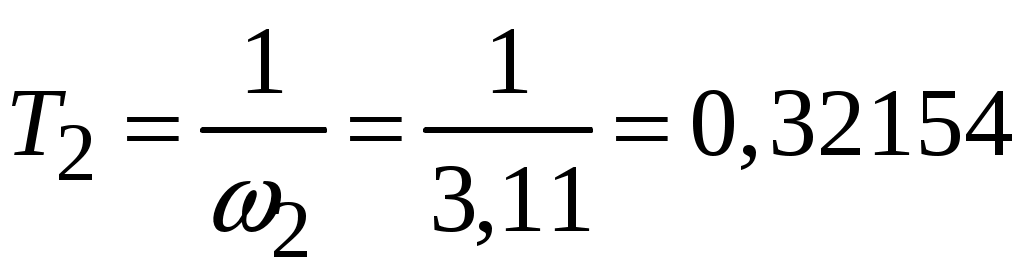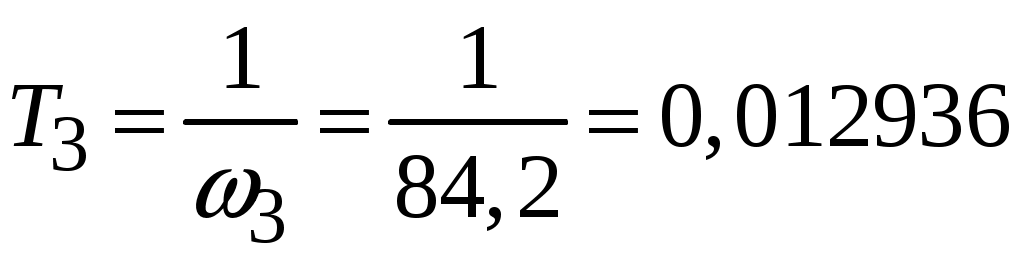с; 
с;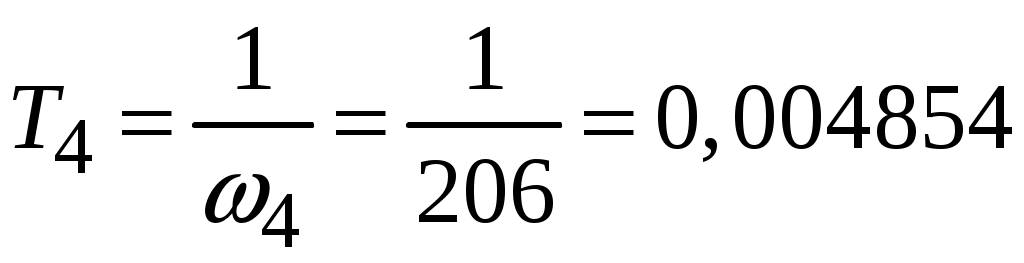 
с;
с.С учётом полученных значений передаточная функция синтезированного регулятора положения принимает вид
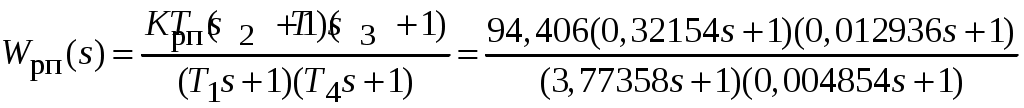.5. Переходим к построению и моделированию ССДМ ЭП, показанной на рис. 4.2. Для формирования линейно возрастающих воздействий
и 
используются блоки Ramp6 и Ramp8.| |
| Рис. 4.2. Структурная схема динамической модели электропривода в среде MatLab |
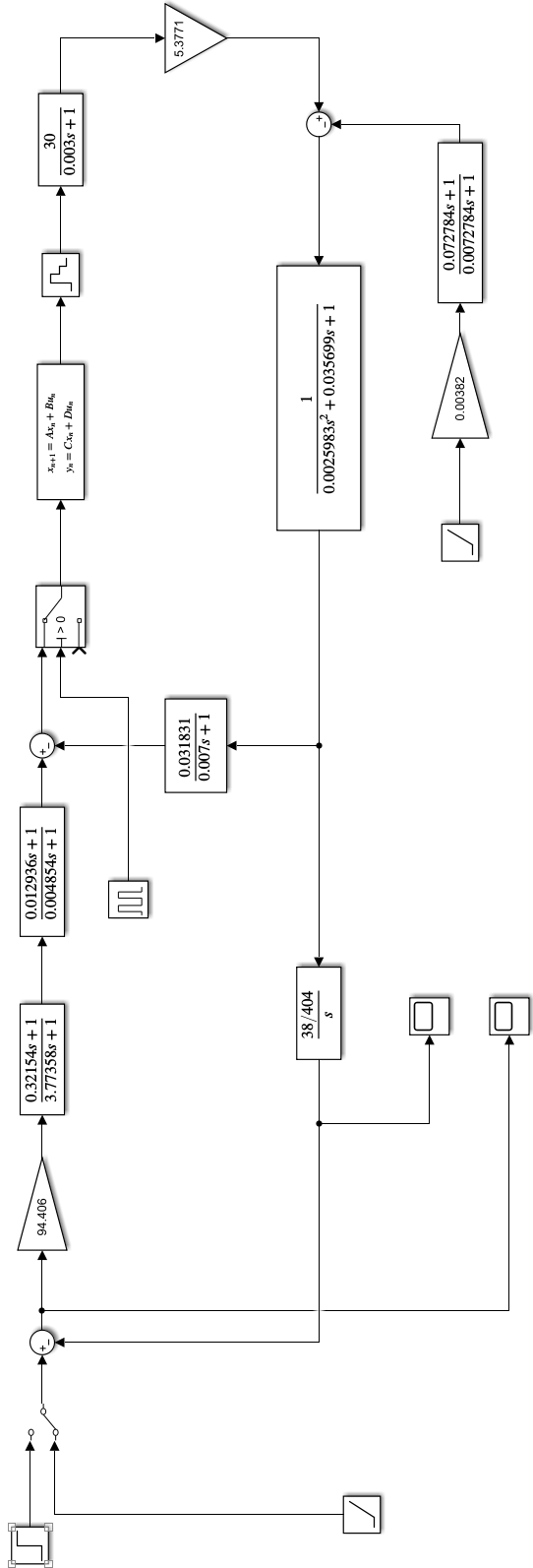
Результаты моделирования показаны на рис. 4.3-4.5.
Анализ графика (рис. 4.3) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие
примерно за 1,5 с, с перерегулированием 
и числом колебаний N < 1, что соответствует заданному показателю колебательности.Поскольку система включает интегрирующее звено на выходе, то очевидно, что статическая ошибка будет равна нулю. На рис. 4.3 представлена характеристика ЭП при линейно возрастающем задающем воздействии. В данном случае ошибка по скорости
составляет 7,48 мин.(Рис. 4.4)α(t), рад
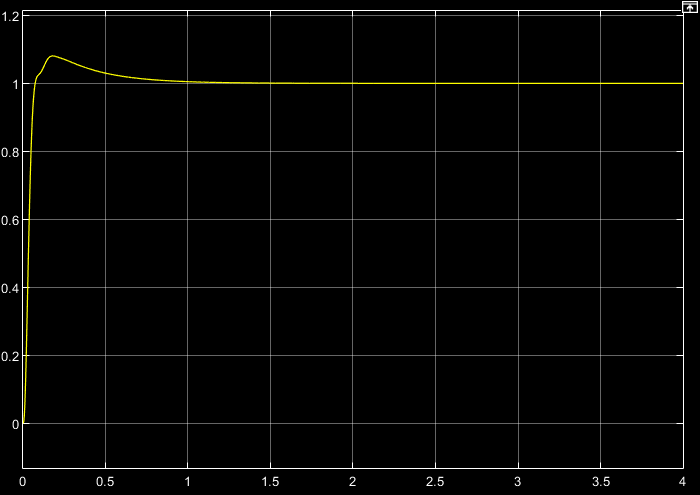t, cРис. 4.3. Переходная характеристика системы по задающему воздействию
, рад
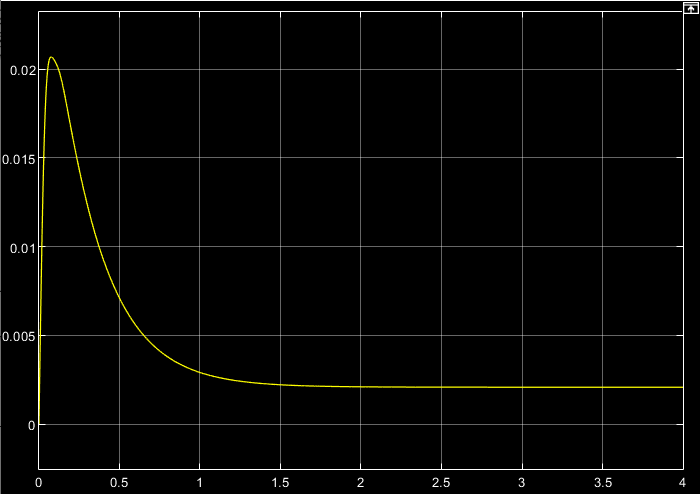t, cРис. 4.4. График ошибки системы при линейно возрастающем задающем воздействии
, рад
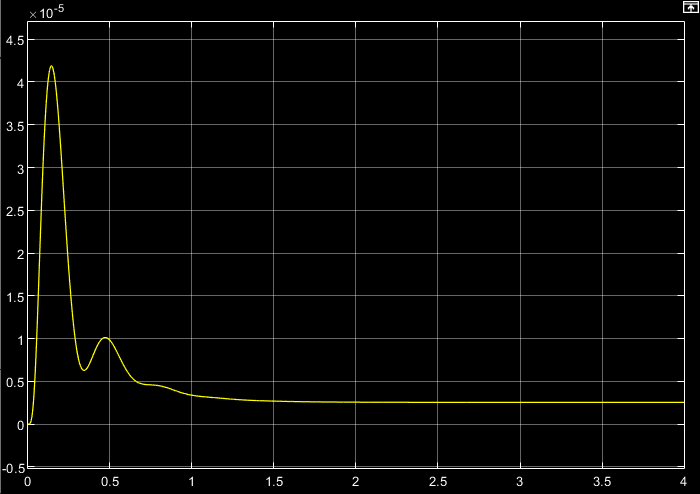
t, cРис. 4.5. График моментной составляющей ошибки системы при линейно возрастающем моменте сопротивления
На рис. 4.5 показан график ошибки, полученный при линейно возрастающем моменте сопротивления Мс. Из графика следует, что влияние возмущающего воздействия сказывается на динамической точности ЭП, а моментная составляющая ошибки
составляет 0,009181 мин по истечении 3 с. При ступенчатом возмущающем воздействии моментная составляющая установившейся ошибки
будет равна нулю.5. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕГУЛЯТОРА ПОЛОЖЕНИЯ
-
Определение алгоритма работы цифрового регулятора положения для электропривода с астатизмом второго порядка.
1.Числовые значения коэффициентов передаточной функции регулятора принять из пункта 4.1 (см. программу 1).
При решении задачи считать период квантования Т0 = 0,001 с.
1. Для упрощения передаточной функции регулятора положения составим программу
num=[14.8 1266 5.409e04 1.131e05 0];
den=[0.3614 68.53 2422 1194 0];
sys=tf(num, den);
minreal(sys)
Transfer function:
40.94 s^3 + 3502 s^2 + 1.497e05 s + 3.13e05
-------------------------------------------
s^3 + 189.6 s^2 + 6701 s + 3303
Для определения передаточной функции цифрового регулятора положения Wрп(z) с применением формулы трапеций (bilinear) составим программу в MATLAB.
num=[40.94 3502 1.497e05 3.13e05];
den=[1 189.6 6701 3303];
Fs=1000;
[numd, dend]=bilinear(num, den, Fs)
numd =
38.9689 -113.576 110.3824 -35.7749
dend =
1.0000 -2.8209 2.648 -0.82708
Запишем передаточную функцию РП относительно переменной z.
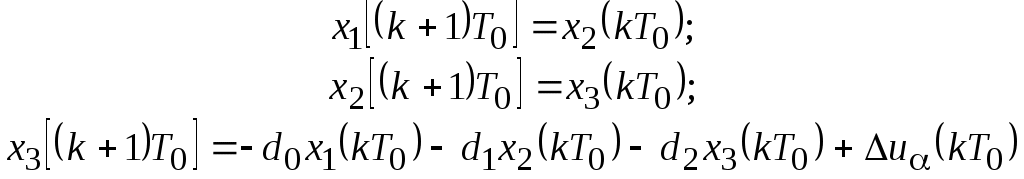
и уравнение выхода
Векторно-матричная форма уравнений цифрового регулятора положения
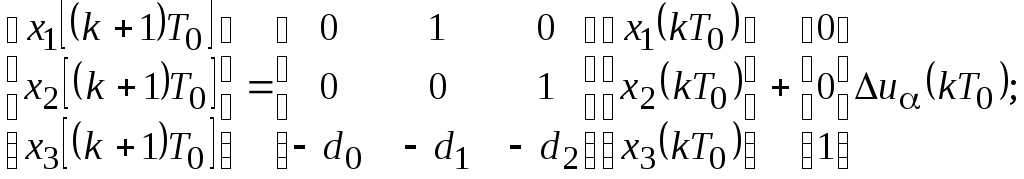
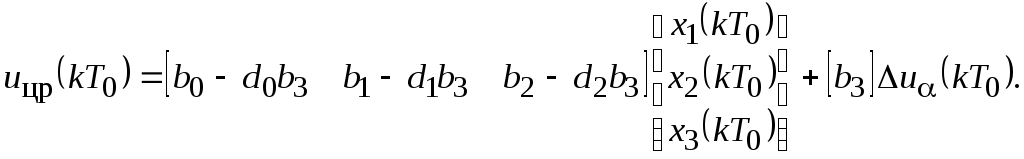
По векторно-матричным уравнениям определяем коэффициенты матриц А, B, C, D соответственно
; 
; 
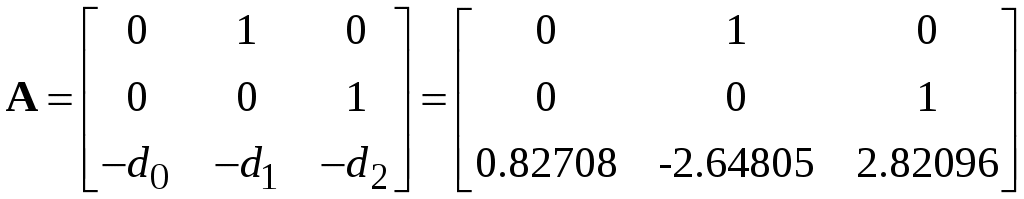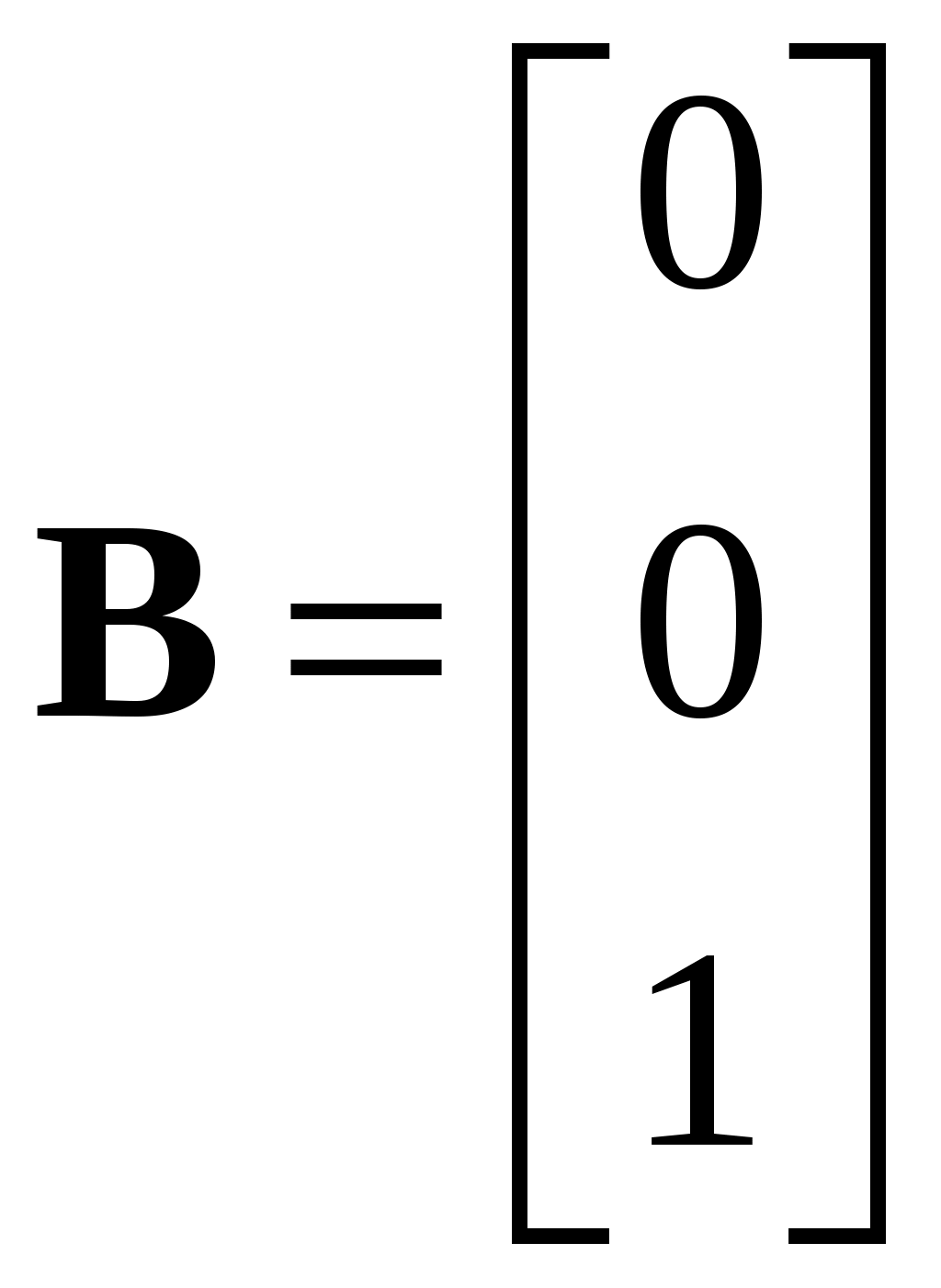.Передаточная функция ИД-регулятора положения записывается как:
.Передаточную функцию цифрового ИД-регулятора положения определим согласно программе.
num=[ 0.3927 31.57695 94.406];
den=[ 0.01831 3.7784 1];
Fs=1000;
[numd, dend]=bilinear(num, den, Fs)
numd =
20.2154 -38.8636 18.6528
dend =
1.0000 -1.81297 0.813
Записываем передаточную функцию цифрового регулятора
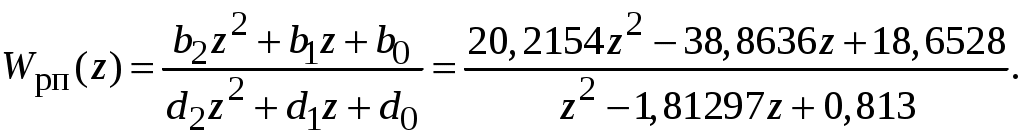
Полученное выражение по своей структуре также совпадает с передаточной функцией цифрового ПИД-регулятора, поэтому для определения соответствующих матриц воспользуемся аналогичными формулами
; 
; 
; 
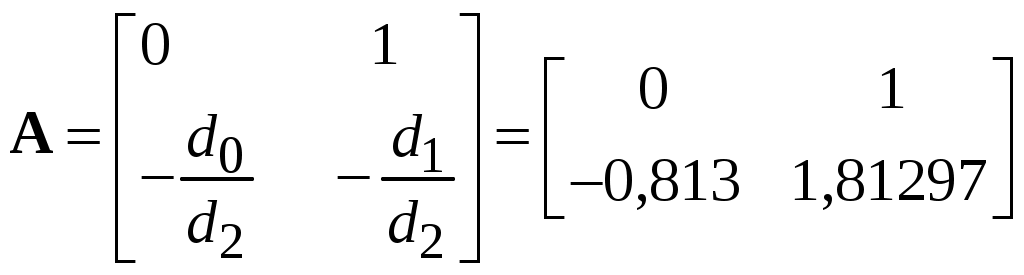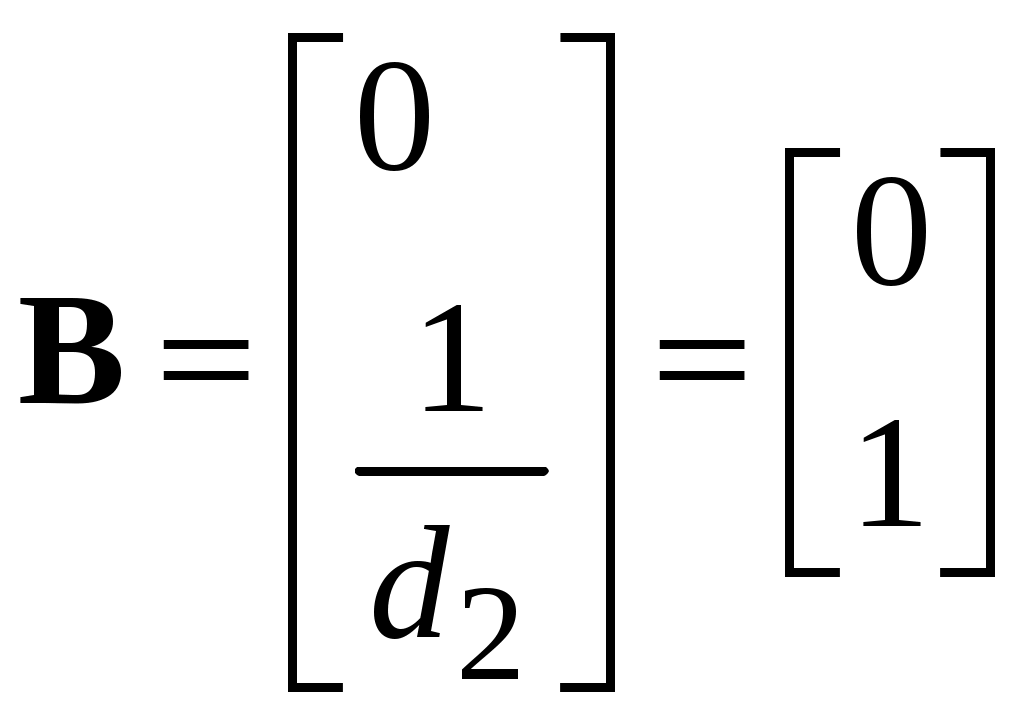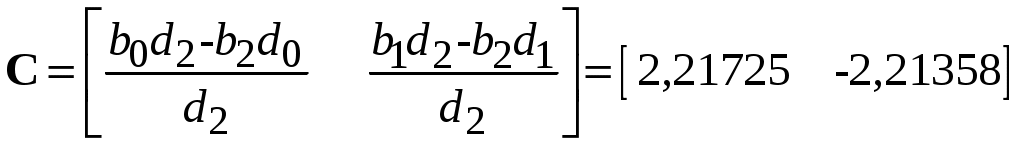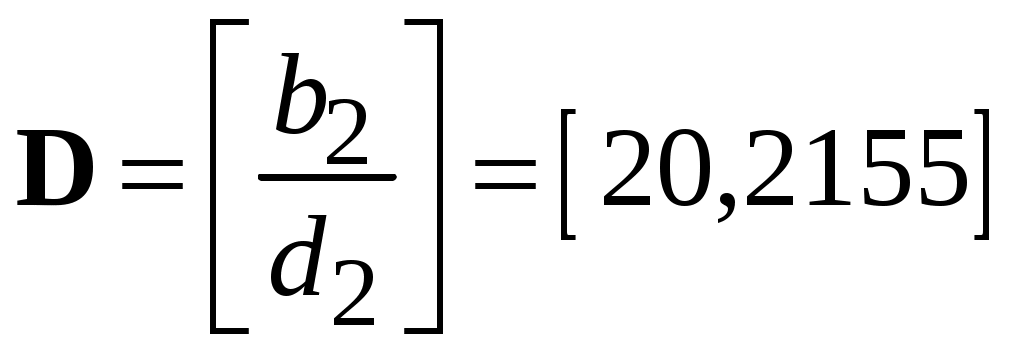.5.2 Моделирование электропривода с астатизмом второго порядка
1. Составляем схему моделирования электроприводов, изображённую на рис. 5.1. В верхней части рисунка показана ССДМ ЭП с цифровым регулятором, синтезированным аналитическим способом (Discrete State-Space1). На рис. 5.2 показано диалоговое окно блока Discrete State-Space1 с матрицами
А, В, С, D и коэффициентами, рассчитанными ранее.
В нижней части рис. 5.1 показана ССДМ ЭП с цифровым ИД-регулятором, синтезированным графоаналитическим способом (Discrete State-Space3). Диалоговое окно блока Discrete State-Space3 с коэффициентами матриц А, В, С, D, рассчитанными ранее, показано на рис. 5.3.
| Рис. 5.1. Схема моделирования электроприводов с астатизмом первого порядка с цифровыми регуляторами положения Discrete State-Space1 и Discrete State-Space3 |
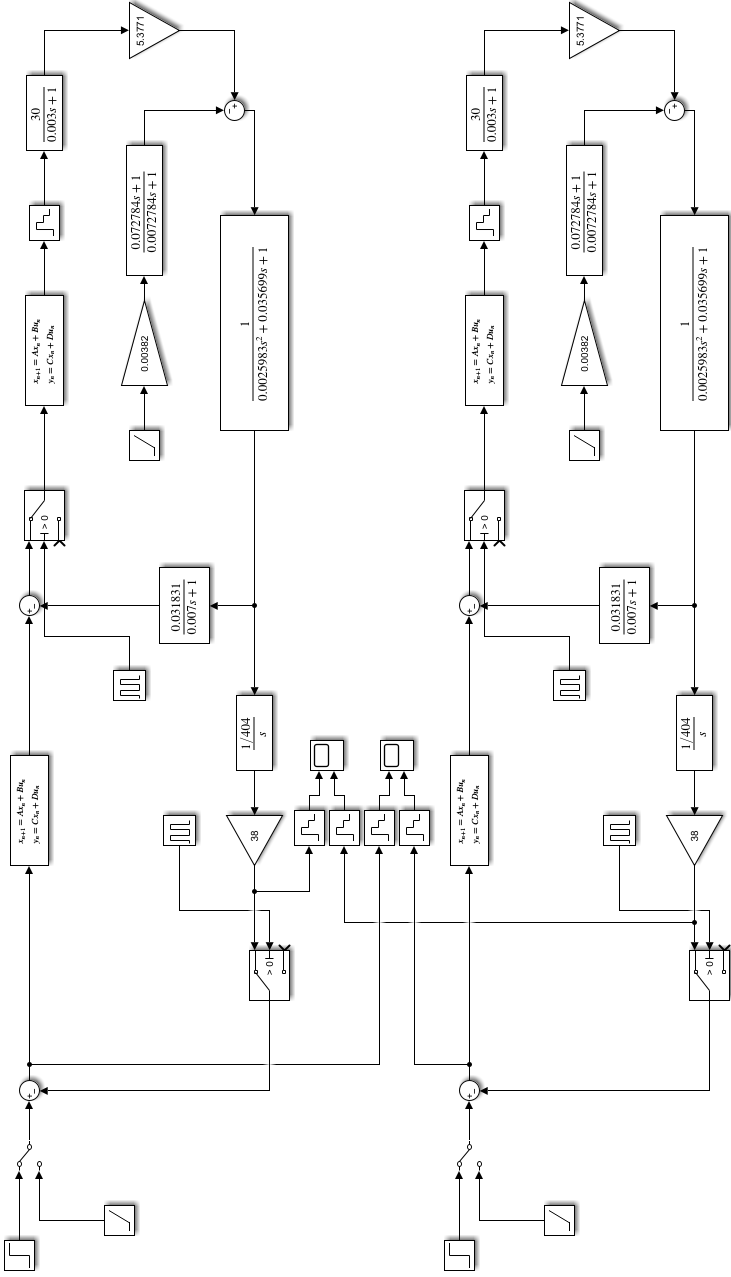
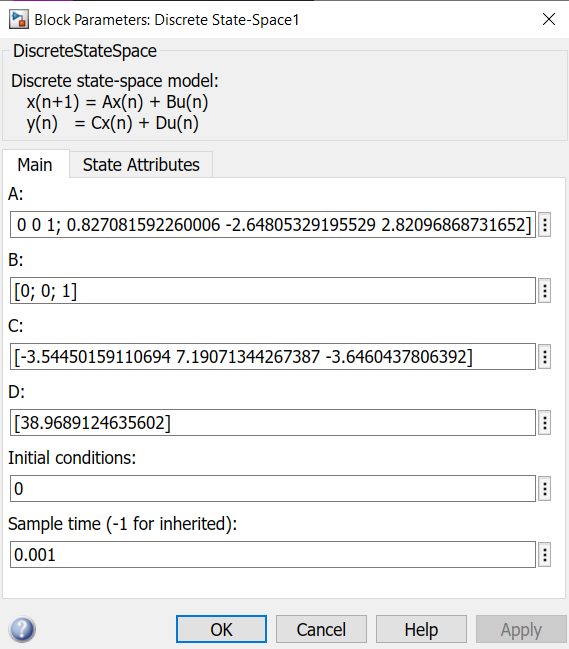
Рис. 5.2. Диалоговое окно блока Discrete State-Space1
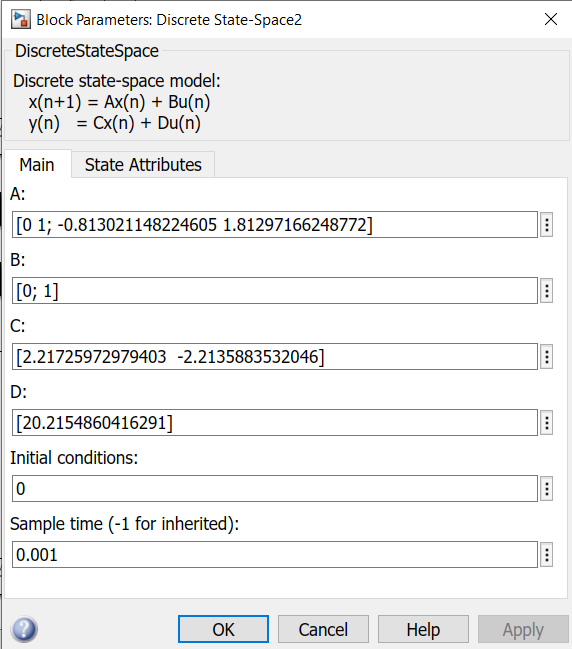
Рис. 5.3. Диалоговое окно блока Discrete State-Space3
-
Проводим моделирование. Для получения переходных характеристик системы по цепи управления в блоках Step и Step1 задаём ступенчатый единичный сигнал. На рис. 5.4 показаны результаты моделирования в виде переходных характеристик системы по задающему воздействию, которые регистрируются блоком Scope1.
α(t), рад
1
2
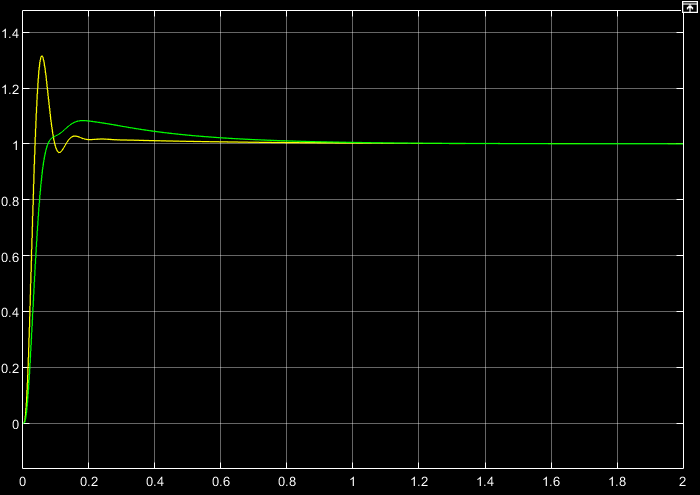
t, cРис. 5.4. Переходные характеристики системы по задающему воздействию
Проведём сравнительный анализ полученных графиков. График 1 является реакцией системы с цифровым регулятором, синтезированным аналитическим способом. График 2 – реакция системы с цифровым ИД-регулятором. Из анализа графиков видно, что перерегулирование в первом случае не превышает 31,5 %; во втором случае перерегулирование составляет 8,3 %. При этом быстродействие ЭП с цифровым ИД-регулятором становится ниже и ПВДУЗ равно 0,076 с, тогда как для графика 1 ПВДУЗ в два раза меньше и составляет примерно 0,037 с. В целом процесс управления с цифровым ИД-регулятором является более плавным, что обеспечивает благоприятный процесс слежения в ЭП.
Для получения графиков ошибок системы на входы ЭП с различными цифровыми регуляторами необходимо подать линейно возрастающее задающее воздействие. На схеме (рис. 5.1) данное типовое воздействие сформировано в виде сигналов с выходов блоков Ramp3 и Ramp4
= 