ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 530
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.62
Из десяти лотерейных билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов: а) один выигрышный; б) оба выигрышных; в) хотя бы один выигрышный.
Из колоды в 36 карт извлекаем две. Какова вероятность того, что это будут две дамы или две черные масти?
Три стрелка произвели залп и одна пуля попала в цель. Найти вероятность того, что третий стрелок попал, если вероятности попаданий этих стрелков равны соответственно: 0,7 , 0,5 , 0,6 .
Допустим, что вероятность рождения девочки 0.49, а мальчика —0.51. Если в семье пятеро детей, то какова вероятность, что в ней три девочки? Какова вероятность, что в семье не менее четырех девочек? Большинство мальчиков?
В урне три шара с номерами 1,2,4. Извлекаем два. Определить закон распределения и числовые характеристики суммы номеров на шарах.
Непрерывная величина задана плотностью
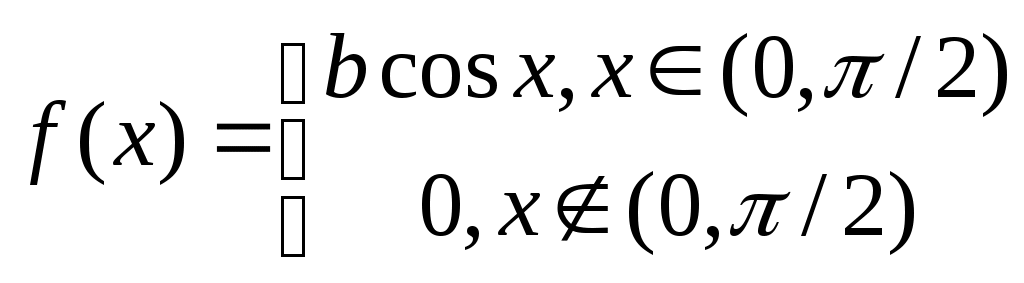
Найти коэффициент b, функцию распределения, числовые характеристики, вероятность события {X<π/4}.
Рост мужчин в некотором регионе есть нормальная с.в. с m=171см и σ=6 см. Какова вероятность того, что случайно встреченный мужчина будет иметь рост:
а) от 169 до 173, б) более179, в) менее 165см?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.63
В зале, насчитывающем n+kмест, случайным образом занимают места п человек. Определить вероятность того, что будут заняты определенные т ≤ п мест.
Для уменьшения общего количества игр 10 команд по жребию разбиваются на две подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной подгруппе.
Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,875.
Найти вероятность попадания при одном выстреле.
Три стрелка делают по три независимых выстрелов по мишени. Вероятности попаданий при одном выстреле для этих стрелков таковы 0,7 , 0,8 , 0,9. Выигрывает тот, кто сделает больше всех попаданий. Найти вероятность ничьей.
Имеем две партии изделий по 100 штук в каждой. В первой партии есть два бракованных изделия, а во второй – четыре. Выбираем по 20 штук из каждой партии и смешиваем. Какова вероятность того, что среди выбранных изделий будут два бракованных?
Вероятность попадания в «десятку» равна 0,1, в «девятку» - 0,3, в «восьмерку» - 0.6. Сделано два независимых выстрела. Найти числовые характеристики суммы очков.
Ошибки вольтметра распределены нормально с дисперсией 10мВ2. Систематической ошибки нет. Найти вероятность того, что ошибка по модулю превзойдет 6мВ. Какова вероятность того, что это произойдет 2 раза в трех измерениях, хотя бы два раза?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.64
Какова вероятность того, что в написанном наугад трехзначном числе две последние цифры одинаковые, а первая нечетна? Какова вероятность получения нечетного числа? Какова вероятность того, что все цифры будут разными?
Из колоды карт (52 карты) наудачу извлекаются три карты. Найти вероятность того, что появится хотя бы один туз.
Имеются пять монет стоимостью по одному рублю,
три по пять и две билета по десять рублей. Наугад берутся три монеты. Определить вероятность того, что: а) хотя бы две из них имеют одинаковую стоимость; б) наберется сумма в семь рублей.
Пару игральных костей бросают 8 раз. Какова вероятность того, что ровно в двух бросках сумма получится равной 11?
На сборку поступают детали от двух поставщиков, причем от второго в два раза меньше. Брак первого поставщика составляет 5%, второго – 3%. Наугад берем две детали. Они оказались годными. Какова вероятность, что они обе от первого поставщика?
Бросаем две правильные пирамидки, на гранях которых написаны цифры 1,2,3,4. Найти закон распределения разности очков первой и второй пирамидок.
Шарик для подшипника считается годным, если он проходит через отверстие с диаметром d1 и не проходит через отверстие с d2. Погрешность в изготовлении нормальна с m=0 и σ=0,001мм. Номинальный диаметр d=7,3мм. Какой процент годных шариков будем иметь, если d1=7,303мм и d2=7,298мм?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.65
Две одинаковые монеты радиуса rрасположены внутри круга радиуса R, в который наудачу бросается точка. Определить вероятность- того, что эта точка упадет на одну из монет, если монеты не перекрываются.
Партия из ста деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной бракованной детали среди пяти проверяемых. Какова вероятность для данной партии быть непринятой, если она содержит 5% неисправных деталей?
Оцените вероятность того, что четырехзначный номер первой встречной машины не содержит а) цифры 5; б) содержит две и более пятерки.
В урне 9 белых и 4 черных шара. Извлекаем 3 шара. Какова вероятность того, что третий будет черным? Какова вероятность того, что третий будет черным, если известно, что первые два разные?
В ящике 3 пары совершенно одинаковых ботинок. Вынимаем наугад по одному ботинку пока не составится пара. Найти закон распределения и числовые характеристики с.в..Х – число вынутых ботинок.
Уровень водохранилища есть нормальная с.в. с m=373м и σ=12,6м. Высота плотины 410м.
Какова вероятность переполнения? Насколько надо поднять плотину, чтобы эта вероятность уменьшилась в два раза?
Станок-автомат изготовляет валики, диаметр которых Х есть нормальная случайная величина с m=8мм и =0,06 мм. найти вероятность того, что диаметр окажется меньше 8 мм. Найти диапазон равных отклонений от требуемого значения диаметра, в котором с вероятностью 0,997 будут находиться диаметры изготовленных валиков.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.66
В ящике 10 пронумерованных деталей. Наугад извлекаем 6 штук. Какова вероятность, что среди них будут детали №3 и №7 ? Какова вероятность, что составится число 537219? То же, но с возвращением деталей.
Изделие может иметь дефект с вероятностью p. Его осматривают последовательно k контролеров. i – ый контролер обнаруживает дефект с вероятностью pi.
При этом изделий сразу бракуется и далее не проверяется. Найти вероятности событий:
А – изделие будет забраковано; В – изделие забракует третий контролер.
Вероятность выхода из строя k-го блока машины за время Т равна pk (k=l, 2, ..., n). Определить вероятность выхода из строя за указанный промежуток времени хотя бы одного из п блоков этой машины, если работа всех блоков взаимно независима.
Два человека по три раза бросают монету. Какова вероятность того, что у обоих герб выпадет ровно по два раза? Какова вероятность того, что у одного из них герб вообще не выпадет, а у другого выпадет менее трех раз?
Стрелок Х поражает мишень с вероятностью 0,6 , стрелок Y – 0,5 , стрелок Z – 0,4. Стрелки выстрелили по разу и две пули попали в цель. Что вероятнее, попал Х или нет?
Диаметр втулки должен быть равен 7,5 мм. Ошибки в изготовлении нормальны с m=0 и =0,04 мм. Если ошибка не превышает по модулю 1% номинального диаметра, то втулка идет первым сортом. Если диаметр гарантирован в пределах [ 7,35; 7,67], то – первым или вторым. Какова вероятность того, что втулка будет второго сорта?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.67
Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производятся последовательно до наступления события. Определить вероятность того, что придется производить четвертый опыт.
Монету подбрасывают три раза. Какова вероятность того, что "решка" выпала три раза, если известно, что по крайней мере один раз выпала "решка"?
Если бейсбольная команда выигрывает с вероятностью 60%, то какова вероятность, что команда одержит победу в трех из пяти игр?
Из трех урн вынимают по одному шару. В первой урне находятся три белых и два черных шара. Во второй — два белых и три черных шара. Третья урна содержит три белых и три черных шара. Если известно, что два из трех вынутых шаров белые, то какова вероятность, что белый шар был вынут из первой урны?
В кузове 768 арбузов. Каждый может оказаться неспелым с вероятностью 0,3. С какой вероятностью число спелых арбузов в партии лежит в пределах от 510 до 690? Превышает 680?
Имеем две независимые дискретные с.в.
С.в. Х с законом
| хi | -2 | 1 | 7 |
| pi | 0,3 | 0,5 | 0,2 |
и с.в. Y c законом
| yk | 0 | 3 | 5 | 6 |
| pk | 0,1 | 0,1 | 0,6 | 0,2 |
Найти их числовые характеристики и числовые характеристики с.в. Z = 2X-Y.
Диаметр втулки должен быть равен 7,5 мм. Ошибки в изготовлении нормальны с m=0 и =0,07 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Если ошибка превышает по модулю 1%, но диаметр в пределах [ 7,40; 7,60], то – вторым. Какова вероятность того, что втулка будет первого или хотя бы второго сорта?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.68
Разрыв электрической цепи может произойти вследствие выхода из строя элемента К или двух элементов К1и К2 ,которые выходят из строя независимо друг от друга соответственно с вероятностями 0,3; 0,2 и 0,2. Определить вероятность разрыва электрической цепи.
Брошены две игральные кости. Найти вероятность того, что сумма очков равна 8, а разность 4. Какова условная вероятность того, что сумма равна 8, если известно, что разность равна 4?
Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, на втором три. Найти вероятность того, что все детали первосортные.