6. 
   Изделие идет первым сортом, если отклонение размера от номинала не превосходят по модулю 3.5 мм. Отклонения нормальны с с.к.о., равным 3 мм. Систематические отклонения отсутствуют. Найти закон распределения и математическое ожидание числа изделий первого сорта, если сделано было 4 изделия.
   

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

Вар.120

1. 
   По каналу связи передаются три сообщения; каждое из них может быть передано с различной степенью точности. Передача одного сообщения может привести к одному из событий:
   

А₁- {сообщение передано правильно};

А₂- {сообщение частично искажено};

А₃ - {сообщение полностью неразличимо}.

Вероятности событий А₁ , А₂ , А₃известны и равны р₁ , р₂, p₃(p₁+ р₂ + p₃ = 1). Считая, что сообщения искажаются (или пере­даются правильно) независимо одно от другого, найти вероятности следующих событий:

В = {все три сообщения переданы без искажений};

С = {хотя бы одно сообщение полностью неразличимо};

D= {не менее двух сообщений искажено полностью или частично}.

2. 
   Какова вероятность, что написанное наугад четырехзначное число содержит одну «семерку»?
   

3. 
   Бросаем три игральные кости. Найти вероятность того, что на них выпали разные числа очков, если известно, что на первой кости выпала «шестерка»?
   

4. 
   Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их мес­тоположения и равны соответственно p₁ ,p₂ ,p₃ . Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут рас­проданы, равна для первой кассы P₁ , для второй Р₂ , для третьей Р₃. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса.
   

---

5. 
   В офисе 6 ламп. Вероятность нормальной работы лампы в течение года равна 0,7. Какова вероятность того, что к концу года будут гореть по меньшей мере три лампы? Чему равно наивероятнейшее число работающих ламп к концу года?
   

6. 
   В коробке семь заготовок. Вероятность сделать годную деталь равна 0,6. Если испортили, то берут следующую заготовку. Найти закон распределения и числовые характеристики числа заготовок, оставшихся после наших попыток сделать одну деталь.
   

7. 
   Рост человека в данной местности есть нормальная с.в. с m=163 и =6. Какова вероятность того, что наудачу выбранный человек имеет рост от 155 до 160 см?, Окажется выше 180 см?
   

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.121

1. 
   На железнодорожной станции пассажиру предоставляется сейф (индивидуальная камера хранения багажа), который открывает­ся только при наборе определенного трехзначного шифра (например, 253, 009, 325 и т. д.). Пассажир набрал шифр, запер сейф и ушел в го­род. Посторонний человек, не знающий шифра, пытается открыть сейф, выбирая три цифры наугад. Найти вероятности событий:
   

А = {сейф откроется с первой же попытки};

В = {сейф откроется после kпопыток}.

2. 
   С конвейера было отобрано 18 изделий и среди них не оказалось брака. Если на самом деле доля брака равна 3%, то какова вероятность этого события?
   

3. 
   Баскетболист попадает в корзину с вероятностью 0,6. Он делает 5 бросков и за каждое попадание получает 50 руб, а за промах отдает 30 руб. Какую сумму он получит с наибольшей вероятностью?
   

4. 
   В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из второго ящика?
   

5. 
   Изделие идет первым сортом, если отклонение размера от номинала не превосходят по модулю 3.5 мм. Отклонения нормальны с с.к.о., равным 3 мм. Систематические отклонения отсутствуют. Найти математическое ожидание числа изделий первого сорта, если сделано было 4 изделия.
   

6. 
   Плотность с.в.Х такова
   

Н

---

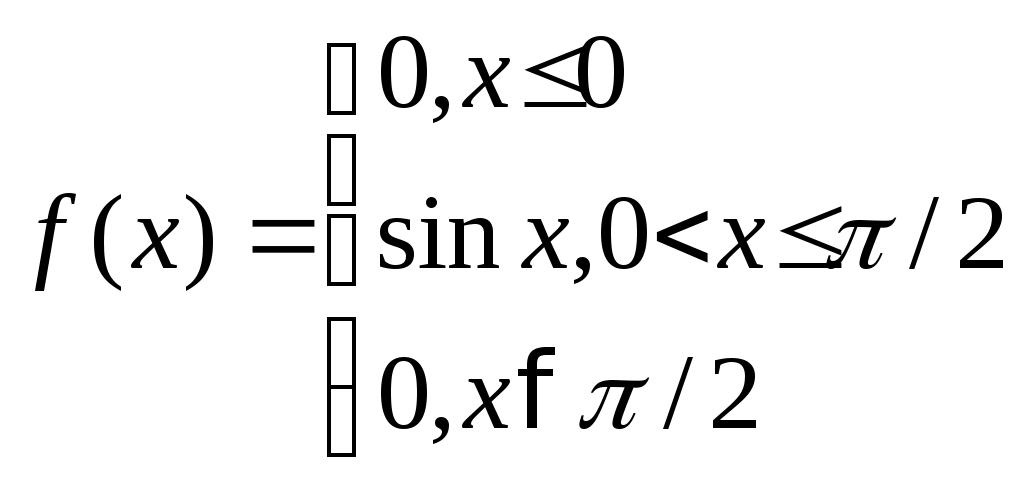
айти функцию распределения, числовые характеристики и вероятность того, что с.в.Х хотя бы раз попадет в интервал (0, π/12) в трех испытаниях.


Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.122
1.Наугад проводим хорду в круге. Какова вероятность того, что ее длина будет больше стороны вписанного в круг равностороннего треугольника?
2.Из 12 лотерейных билетов, среди которых есть 4 выигрышных, наудачу берут 6. Какова вероятность того, что хотя бы один из них выигрышный?
3.Рассчитать вероятность отказа цепи (не идет ток),



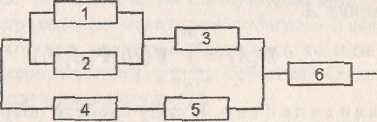
где pi - вероятность отказа г-го элемента.
4.В ящике 3 белых и 7 черных шаров. Один шар вынули наудачу и отложили в сторону. Следующий наугад вынутый шар оказался белым. Какова вероятность того, что отложенный шар был белым?
5.На пути автомобиля четыре светофора. каждый из них запрещает движение с вероятностью 0,4 независимо от других . Определить закон распределения и числовые характеристики с.в.Х – число светофоров, пройденных без остановки.
6.Случайная величина Xимеет плотность распределения



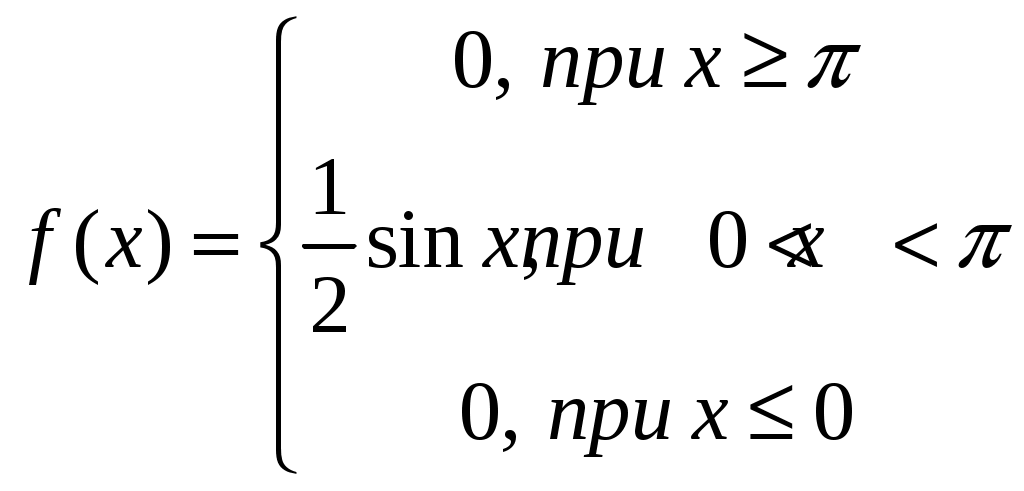
а) Определить функцию распределения F{x)

б) найти вероятность того, что величина Xпримет значение, заключенное в интервале (0, π/4).


7. Рост мужчин в некотором регионе есть нормальная с.в. с m=171см и σ=6 см. Какова вероятность того, что случайно встреченный мужчина будет иметь рост:

а) от 169 до 173, б) более179, в) менее 165см?

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

---

Вар.123
Если десять карт последовательно вытягиваются из колоды, то какова вероятность, что две карты окажутся червовыми?

Для уменьшения общего количества игр 10 команд по жребию разбиваются на две подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной под­группе.

Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,875.

Найти вероятность попадания при одном выстреле.

Три стрелка делают по три независимых выстрелов по мишени. Вероятности попаданий при одном выстреле для этих стрелков таковы 0,7 , 0,8 , 0,9. Выигрывает тот, кто сделает больше всех попаданий. Найти вероятность ничьей.

Имеем две партии изделий по 100 штук в каждой. В первой партии есть два бракованных изделия, а во второй – четыре. Выбираем по 20 штук из каждой партии и смешиваем. Какова вероятность того, что среди выбранных изделий будут два бракованных?

Вероятность попадания в «десятку» равна 0,1, в «девятку» - 0,3, в «восьмерку» - 0.6. Сделано два независимых выстрела. Найти числовые характеристики суммы очков.

Ошибки вольтметра распределены нормально с дисперсией 10мВ². Систематической ошибки нет. Найти вероятность того, что ошибка по модулю превзойдет 6мВ. Какова вероятность того, что это произойдет 2 раза в трех измерениях, хотя бы два раза?

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

Вар.124
Пару игральных костей бросают 8 раз. Какова вероятность того, что ровно в двух бросках сумма получится равной 11?

Из колоды карт (52 карты) наудачу извлекаются три карты. Найти вероятность того, что появится хотя бы один туз.

Имеются пять монет стоимостью по одному рублю,

три по пять и две билета по десять рублей. Наугад берутся три монеты. Определить вероятность того, что: а) хотя бы две из них имеют одинаковую стоимость; б) наберется сумма в семь рублей.

Пару игральных костей бросают 8 раз. Какова вероятность того, что ровно в двух бросках сумма получится равной 11?

---

На сборку поступают детали от двух поставщиков, причем от второго в два раза меньше. Брак первого поставщика составляет 5%, второго – 3%. Наугад берем две детали. Они оказались годными. Какова вероятность, что они обе от первого поставщика?

Бросаем две правильные пирамидки, на гранях которых написаны цифры 1,2,3,4. Найти закон распределения разности очков первой и второй пирамидок.

Шарик для подшипника считается годным, если он проходит через отверстие с диаметром d₁ и не проходит через отверстие с d₂. Погрешность в изготовлении нормальна с m=0 и σ=0,001мм. Номинальный диаметр d=7,3мм. Какой процент годных шариков будем иметь, если d₁=7,303мм и d₂=7,298мм?

Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.

Вар.125


Две одинаковые монеты радиуса

---

Смотрите также файлы

• Существенным фактором для любой хорошо функционирующей социальной системы являются социальная защита, социальная и экономическая поддержка населения.docx

• 1 Теоретические и методические аспекты анализы прибыли и ее налогообложения.docx

• Начальник пожарной части Зам начальника пожарной части Старшина части.docx

• Законе рф О защите прав потребителей.docx

• Тема Функции и методы, структура и документы стандартизации.docx