ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 531
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков. Разные числа очков?
Отдел технического контроля проверяет изделия. Вероятность брака – 0,1. Найти вероятность того, что из трех проверенных лишь одно окажется бракованным. Какова вероятность того, что хотя бы одно будет бракованным?
Предположим, что мы играем в рулетку, на ячейках которой написаны числа от 0 до 36. Заплатив 1 доллар, вы можете получить 36, если угадаете ячейку. Найдите математическое ожидание своего выигрыша и проигрыша.
Ошибка в изготовлении детали нормальна с с m=0,1мм и σ=0,15мм. Если ошибка по модулю не превосходит 0,3мм, то деталь можно использовать. Изготовлено 7 деталей.
Найти ожидаемое число годных. Какова вероятность того, что негодных будет более половины?
Производились наблюдения за числом вторжений в минуту. Наблюдения в течение часа дали следующие результаты:
3, 1, 3, 4, 2, 1, 1, 3, 2,7, 2, 0, 1, 2, 1,
2, 4,0, 3, 0, 2, 0, 1, 3, 3, 1, 2, 0, 3, 4,
-
0, 2, 1, 4, 3, 4, 2, 0, 2, 3, 1, 1, 2,2, -
1, 4, 2, 2, 1, 2, 5, 1, 1, 0, 1, 1, 1, 5.
Оценить среднее и дисперсию количества спама в минуту.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.76
Четырехтомное сочинение расположено на полке в случайном порядке. Какова вероятность того, что тома стоят в правильном порядке справа налево или слева направо?
В ящике 20 шаров с номерами 1, 2, … ,20. Наугад выбираем шесть. Какова вероятность того, что среди них есть шары с номерами 7 и 13? Какова вероятность того, что на половине извлеченных будут четные номера?
Подбрасываются две кости. Какова вероятность того, что сумма значений на кубике равна 8, если известно, что сумма больше или равна 7?
В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из первого ящика?
Текст содержит 20000 букв. Каждая буква может быть напечатана неправильно с р=0,0004. Какова вероятность того, что в тексте не менее двух опечаток?
Предположим, что картам присвоены такие стоимости: туз имеет стоимость 1, двойка — 2, ..., десятка — 10, валет — 11, дама — 12, король — 13. Игрок вытягивает карту.
Если вытянута карта червовой масти, то игрок получает удвоенную стоимость карты. Если это карта бубей, он получает стоимость карты. Если карта черной масти, то игрок платит $10. Каково математическое ожидание выигрыша в этой игре?
Деталь, изготовленная автоматом, считается годной, если ее отклонение от номинала не более 0,1 мм. Эти отклонения нормальны с m=0 и σ=0,05мм. Какой процент годных деталей дает автомат? Какова вероятность того, что из 5 деталей хотя бы 2 годные?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.77
Стрелок производит один выстрел в мишень, состоящую из центрального круга и двух концентрических колец. Вероятности попадания в круг и кольца соответственно равны 0,20, 0,15 и 0,10. Определить вероятность непопадания в мишень.
Какова вероятность извлечь из колоды в 52 карты фигуру любой масти или карту пиковой масти? (фигурой называется валет, дама или король)
Из стандартной колоды с 52 картами вытягивают две карты. Какова вероятность того, что вторая карта — король, если известно, что первая карта - туз? Какова вероятность того, что вторая карта — король, если известно, что первая карта — туз пик?
Игрок попадает по мячу один раз из трех. Какова вероятность, что он попадет три раза из десяти?
В коробке 4 новых и 3 использованных теннисных мяча. Наудачу берем два, играем и возвращаем в коробку. Какова вероятность в следующий раз вынуть два использованных мяча?
В урне 5 белых и 22 черных шаров. Вынули 3 шара. Случайная величина Х – число вынутых белых шаров. Построить закон распределения и функцию распределения величины X.
Шарик для подшипника считается годным, если он проходит через отверстие с диаметром d1 и не проходит через отверстие с d2. Погрешность в изготовлении нормальна с m=0 и σ=0,001мм. Номинальный диаметр d=7,3мм. Какой процент годных шариков будем иметь, если d1=7,303мм и d2=7,298мм?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.78
В колоде 52 карты. Какова вероятность:
а)вытянув две карты получить сначала туза, а потом короля?
б)вытянув две карты, получить туза и короля?
в)вытянув пять карт получить не менее двух тузов?
г)вытянув одну карту получить либо туза, либо пики?
В ящике имеются 10 монет по 20 коп., 5 монет по 15 коп. и 2 монеты по 10 коп. Наугад берутся шесть монет. Какова вероятность, что в сумме они составят не более одного рубля?
Монету бросаем до тех пор пока не выпадут подряд два герба или две решки. Какова вероятность того, что понадобится более семи бросков?
В офисе 4 лампы. Вероятность нормальной работы лампы в течение года равна 0,8. Какова вероятность того, что к концу года будут гореть по меньшей мере три лампы? Чему равно наивероятнейшее число работающих ламп к концу года?
Имеем две партии изделий по 100 штук в каждой. В первой партии есть два бракованных изделия, а во второй – четыре. Выбираем по 20 штук из каждой партии и смешиваем. Какова вероятность того, что среди выбранных изделий будут два бракованных?
Ошибки вольтметра распределены нормально с дисперсией 10мВ2. Систематической ошибки нет. Найти вероятность того, что ошибка по модулю превзойдет 6мВ. Какова вероятность того, что это произойдет 2 раза в трех измерениях, хотя бы два раза?
Дана функция распределения случайной величины Х
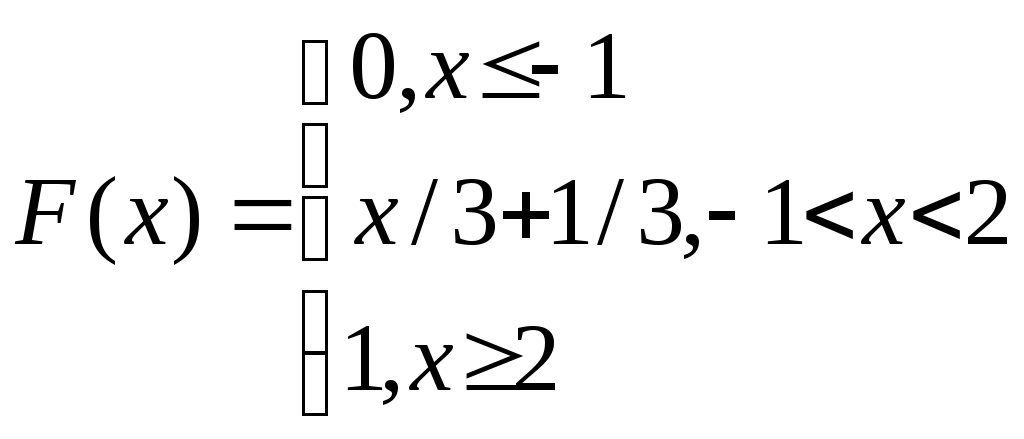Найти плотность распределения, числовые характеристики. Найти вероятность P{0≤X≤1}.Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.79
Внутри отрезка [a , b] лежит точка c. На этот отрезок наудачу ставят еще три точки.
Рассматриваются следующие события:
C - одна точка - на [ a , c ], а две другие - на ( c , b ];
F - хотя бы одна точка - на ( c , b ];
G - не менее двух точек - на [ a , c ].
Найти вероятность (GC)F.
Из пачки в десять билетов выигрышными являются два. Наугад вынимаем 5 билетов. Какова вероятность того, что среди них 1 выигрышный? То же, но при возвращении каждого билета обратно в пачку и перемешивании.
Уровень водохранилища есть нормальная с.в. с m=373м и σ=19,6м. Высота плотины 410м.
Какова вероятность переполнения? Насколько нужно поднять плотину, чтобы эта вероятность стала менее 0,01?
Прибор содержит четыре узла: А1, А2, А3, А4. Узел А1дублирует А2 , а А3 дублирует А4. При отказе происходит автоматическое переключение. Надежность переключающего устройства равна р. Надежность в течение заданного времени каждого из узлов равна pi , i= 1,2,3,4
. Вычислить надежность прибора.
Объект, за которым ведется наблюдение, может находиться в одном из двух состояний: Н1 и Н2; априорные вероятности этих состояний Р (Н1) = 0,3; Р (Н2) = 0,7. Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта: первый источник сообщает, что объект находится в состоянии Н1второй — что в состоянии Н2. Первый источник вообще дает правильные сведения о состоянии наблюдаемого объекта в 90% случаев и только в 10% ошибается. Второй источник менее надежен: он сообщает правильные сведения в 70% случаев, а в 30% ошибается. На основе анализа донесений найти новые (апостериорные) вероятности состояний
Н1 и Н2 .
Сколько нужно взять чисел из таблицы случайных чисел, чтобы с вероятностью не менее 0,9 быть уверенным, что среди них хотя бы одно число четное?
Рост мужчин в некотором регионе есть нормальная с.в. с m=171см и σ=6 см. Какова вероятность того, что случайно встреченный мужчина будет иметь рост:
а) от 169 до 173, б) более179, в) менее 165см?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.80
В пачке 10 лотерейных билетов и из них два выигрышных. Наугад вынимаем пять. Какова вероятность того, что среди них один выигрышный? Какова вероятность этого же события при условии, что мы возвращаем каждый билет в пачку, перемешиваем и снова извлекаем и так повторяем пять раз?
В лифте 9-и этажного дома поднимаются 8 человек. На любом этаже, начиная с третьего каждый может выйти с вероятностью p. Какова вероятность того, что все доедут до девятого ? Какова вероятность того, что хотя бы один доедет до девятого ?
Отрезок разделен не три равные части. На отрезок наугад бросают три точки. Какова вероятность того, что на каждую из частей попадет по одной точке? Какова вероятность того, что все точки попадут на одну из частей отрезка?