ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 534
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В первом ящике 5 годных и 7 дефектных деталей, а во втором 9 годных и 3 дефектные. Детали смешивают и извлекают наугад две. Они оказались дефектными. Какова вероятность того, что они из второго ящика?
Батарея произвела 6 выстрелов по объекту. Вероятность попадания при одном выстреле равна 0,3. Найти наивероятнейшее число попаданий. Найти вероятность разрушения объекта, если для этого достаточно двух попаданий.
Производится два независимых измерения. Погрешность измерения нормальна с m=10мВ и σ=30мВ. Какова вероятность того, что обе ошибки измерения, имея разные знаки, превзойдут по абсолютной величине 12мВ?
Станок-автомат изготовляет валики, диаметр которых Х есть нормальная случайная величина с m=5мм и =0,04 мм. найти вероятность того, что диаметр окажется меньше 6 мм. Найти диапазон равных отклонений от требуемого значения диаметра, в котором с вероятностью 0,997 будут находиться диаметры изготовленных валиков.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.69
На полке 15 книг. 4 из них в переплете. Наугад берем 3. Какова вероятность того, что хотя бы одна из них в переплете?
Работа прибора прекратилась вследствие выхода из строя одного элемента из общего числа N. Отыскание этого элемента производится путем поочередной проверки каждого элемента. Определить вероятность того, что придется проверять п элементов, если вероятности выхода из строя у них всех одинаковы.
В городе четыре библиотеки. Вероятность того, что нужная книга есть в библиотеке равна 0,2, а вероятность того, что она при этом не выдана равна 0,7. Найти вероятность того, что мы получим книгу.
Из 18 стрелков 5 попадают с вероятностью 0,8; 7 – с вероятностью 0,7; 4 – с вероятностью 0,6; 2 – с вероятностью 0,5. Наугад выбранный стрелок выстрелил и не попал. К какой из четырех групп стрелков он принадлежит с наибольшей вероятностью?
Производится два независимых выстрела по мишени. Вероятность попадания при каждом равна р. Найти числовые характеристики с.в. Х – разность между числом попаданий и числом промахов.
Случайная величина Xимеет плотность распределения
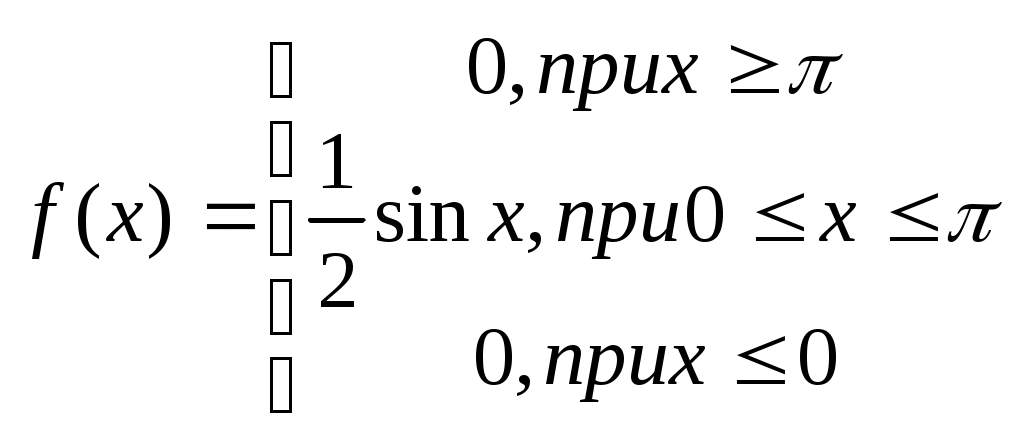
а) Определить функцию распределения F{x)
б) найти вероятность того, что величина Xпримет значение, заключенное в интервале (0, π/4).
Ошибки прибора распределены нормально с нулевым математическим ожиданием и с.к.о. равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза из пяти измерений? Хотя бы два раза?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.70
На шахматную доску случайным образом ставят две ладьи. Какова вероятность того, что они не «бьют» друг друга? То же для случая двух слонов.
Из колоды в 52 карты последовательно извлекают 4. Найти вероятность того, что они будут разных мастей. Вероятность того, что выйдут два туза и две дамы. Вероятность того, что ровно 2 из них будут пиковым.
Четыре туза из стандартной колоды перетасованы и разложены на столе картинкой вниз. Две карты, не раскрывая, убирают. Какова вероятность, что третья карта — туз пик?
Если монету подбрасывают семь раз, то какова вероятность выпадения четырех "решек"?
Один игрок бросает 3 монеты, а другой – 2. найти закон распределения случайной величины Х разность числа гербов, выпавших у первого и второго игроков. Найти числовые характеристики с.в.Х.
Непрерывная величина задана плотностью
Н
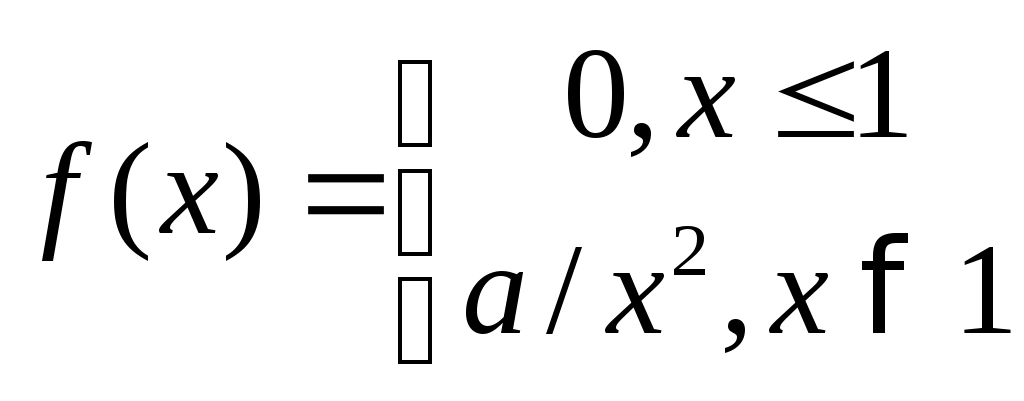
айти коэффициент а, функцию распределения, вероятность события {2<X<3}.
Ошибки прибора распределены нормально с нулевым математическим ожиданием и с.к.о. равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза из пяти измерений? Хотя бы два раза?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.71
Пару игральных костей бросают 8 раз. Какова вероятность того, что ровно в двух бросках сумма получится равной 11?
Вероятность того, что в результате четырех независимых опытов событие А произойдет хотя бы один раз, равна 0,5. Определить вероятность появления события при одном опыте, если она во всех опытах остается неизменной.
Бросается игральная кость. Если результат делится на три, то это "выигрыш". Какова вероятность выиграть 2 раза из пяти бросков? Какова вероятность выиграть хотя бы раз?
Расследуются причины авиакатастрофы, о которых можно сделать 4 гипотезы: H1, H2, H3, H4. Согласно статистике P(H1)=0,2 , P(H2)=0,4 , P(H3)=0,3 , P(H4)=0,1. Вероятности воспламенения при выполнении гипотез равны соответственно 0,9 , 0 , 0,2 , 0,3. Известно, что воспламенения не было. Какая гипотеза вероятнее других?
Какова вероятность того, что из 1000 человек в конкретный день родились
а) ни одного, б) один, в) два, г) три человека?
В урне три шара с номерами 1,2,3. Извлекаем два. Определить закон распределения и числовые характеристики с.в. х – модуль разности номеров первого и второго шаров.
Станок-автомат изготавливает валики, диаметр которых Х есть нормальная случайная величина с m=10мм и =0,15мм. найти вероятность того, что диаметр окажется меньше 10,07мм. Найти диапазон равных отклонений от математического ожидания, в котором с вероятностью 0,9973 будут находиться диаметры изготовленных валиков.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.72
Если десять карт последовательно вытягиваются из колоды, то какова вероятность, что две карты будут червовыми?
Вероятность того, что в электрической цепи напряжение превысит номинальное значение, равна p1 .При повышенном напряжении вероятность аварии прибора — потребителя электрического тока равна р2 .Определить вероятность аварии прибора вследствие повышения напряжения.
Среди 30 экзаменационных билетов есть 20 легких. Каким по очереди Вам выгоднее тянуть билет первым, вторым, третьим и т.д.?
Бросается игральная кость. Если результат делится на три, то это "выигрыш". Какова вероятность выиграть 2 раза из пяти бросков? Какова вероятность выиграть хотя бы раз?
Четвертая часть только одной из пяти партий является второсортной. Деталь, взятая из какой-то партии, оказалась первосортной. Какова вероятность того, что она из партии, в которой есть второсортные.
Два баскетболиста поочередно бросают мяч в корзину до первого попадания. Вероятность попадания первого – 0,4, а второго – 0,7. Найти закон распределения числа бросков до первого попадания.
Ошибки прибора распределены нормально с нулевым математическим ожиданием и с.к.о. равным 3. Какова вероятность того, что ошибка по модулю превзойдет 6? Какова вероятность того, что это произойдет лишь два раза из пяти измерений? Хотя бы два раза?
По 12 независимым измерениям посчитано среднее арифметическое скорости 424,7 м/с. Определить 90%-й доверительный интервал для ожидаемой скорости, если прибор имеет нормальную ошибку с с.к.о. , равной 2,5м/с. Систематической ошибки нет.
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.73
Слово «Миссисипи» разрезаем на буквы и наугад выкладываем по одной в ряд. Какова вероятность того, что все гласные окажутся стоящими рядом? Какова вероятность того, что все согласные станут рядом?
Если 10% продукции составляют брак, то какова вероятность получить два бракованных изделия среди выбранных десяти изделий?
Вероятность выигрыша по одному лотерейному билету p = 0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному с вероятностью 0,99?
Стрелок Х поражает мишень с вероятностью 0,6 , стрелок Y – 0,5 , стрелок Z – 0,4. Стрелки выстрелили по разу и две пули попали в цель. Что вероятнее, попал Y или нет?
Завод отправил в магазин 5000 бокалов. Вероятность разбить бокал при транспортировке равна 0,0002. Найти вероятность того, что разобьются не более трех.
Шесть шаров пронумерованы числами 0, 0, 0, 0, 10 и 20 и помещены в урну. Произвольным образом выбирается один шар, и если этот шар имеет номер п, то игрок получает п долларов. Каково математическое ожидание выигрыша?
Диаметр втулки должен быть равен 7,5 мм. Ошибки изготовления нормальны с m=0 и =0,05 мм. Если ошибка не превышает по модулю 1%, то втулка идет первым сортом. Какова вероятность того, что втулка будет первого сорта? Какова вероятность того, что из пяти втулок хотя бы 3 будут первосортными?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.74
В круг радиуса R вписан правильный треугольник. Затем внутрь круга наугад брошены 4 точки. Найти вероятности следующих событий: а) все 4 точки не попали в треугольник, б) две в треугольнике и две в каком-то малом сегменте.
С помощью шести карточек, на которых написано по одной букве, составлено слово «карета». Карточки перемешиваются, а затем наугад извлекаются по одной. Какова вероятность того, что в порядке поступления букв образуется слово «ракета»?
В урне п пронумерованных от 1 до и одинаковых шаров. Производится т извлечений шаров по одному с возвращением. Определить вероятность того, что ни разу не будет извлечен шар с одним и тем же номером.
В урне содержится восемь белых и семь черных шаров. Вынимается четыре шара без возвращения. Какова вероятность, что первый шар белый, если известно, что было вытянуто два белых шара?
Вероятность рождения мальчика 0,515. Какова вероятность того, что среди 10000 новорожденных мальчиков не больше, чем девочек? (Использовать предельные теоремы)
В игре подбрасывают два кубика. Игрок получает сумму рублей, равную сумме значений на кубиках. Сколько может стоить участие в этой игре?
Отклонение размера детали от номинала подчинено нормальному закону с m=0 и σ=0,12мм. Если отклонение Δх < 0,02 , то деталь годится дли изделий №1. Если отклонение –0,01< Δх < 0,03, то для изделия №2. Какова вероятность того, что деталь можно будет использовать? Какова вероятность того, что деталь подойдет для обеих изделий?
Типовой расчет следует выполнять на скрепленных листах формата А4. Условия задач переписывать и давать решение на отдельном листе с комментариями, оставляя место для замечаний и исправлений. Все вычисления проводить с точностью до 0.001. Задание должно быть приложено. Требования для титульного листа стандартные. Крайний срок сдачи – 15 неделя.
Вар.75
Слово «паркет» разрезается на буквы. Затем выбираем наугад 4 буквы и выкладываем на стол в порядке появления. Какова вероятность того, что третья буква в полученном наборе «а»? Какова вероятность того, что первая «р», а последняя «а»?