2μ34дт2μмяя+++++++ + = Осуществляем подстановку значений в передаточную функцию неизменяемой части (р)Wнч: р1045,0р1077.5р1045.9р107.56 )104,0(136,0 )( 233547-+++ + = −−ppWнчОпределим полюсы передаточной функции неизменяемой части ( ):pWнч????1= 0; ????2= −28.185; ????3= −48.407 − 50.596????; ????4= −48.407 + 50.596????; Разобьем передаточную функцию на отдельные звенья: 102,010039.2 1 1035,0 1)104,0(302,1 )( 24++  + + = −ppppppWнчЗдесь )(pWрс - передаточная функция корректирующего устройства (регулятора), (p)Wнч - передаточная функция неизменяемой части, включающая звенья, входящие в w wз Wнч(p) Wрс(p) Рис. 4. Структурная расчетная схема САУ замкнутый контур тока, т.е. (p)Wрт, (p)Wтп, (p)Wд1, (p)Wдт, и звено объекта управления (p).Wд2

---

1.2 Построение частотных характеристик объекта регулирования (неизменяемойчасти системы):Передаточная функция неизменяемой части представлена в виде произведения передаточных функций типовых звеньев: изодромного, апериодического и колебательного звена. Построив ЛАЧХ каждого звена и просуммировав их, мы получим ЛАЧХ неизменяемой части. pp)104,0(302,1 (p)W1+ = -изодромное звено: k1=1.302; Т1=0,04 с; 1ω =25 рад/с; 1035,0 1 (p)W2+ = p- апериодическое звено: k2=1; Т2=0,035 с; 2ω =28,571 рад/с; 1714,0014,02014,0 1 (p)W 223++ = pp- колебательное звено k3=1; Т3=0,014 с; 3ω =71.43 рад/с; ξ =0,714; Все построения частотных характеристик выполнены в диапазоне от 1 до 1000 с-1. Для построения характеристик были выбраны следующие масштабы: по частоте – 1 декада на 100 мм; по усилению – 10 дБ на 10 мм; по фазе – 900 на 30 мм. Для построения фазовых характеристик выбираем частоты ω в диапазоне  111000с1с −− :        −= ω0,04 1 arctg) (ω1 - ЛФЧХ изодромного звена; ( )ω0,035arctg) (ω2−= - ЛФЧХ апериодического звена;           −= 231ω)(0,014-1 ω0,02 arctg) (ω - ЛФЧХ колебательного звена при ω<1/Т;       −−= 232ω)(0,014-1 ω0,02 arctgπ) (ω - ЛФЧХ колебательного звена при ω>1/Т 3210 ++= - ЛФЧХ неизменяемойчасти( объекта)        −= ω0,1 1 arctg) (ωр - ЛФЧХ регулятора скорости; р0ж1 += - ЛФЧХ желаемой части Таблица 1 - Расчет ЛФЧХ ω , с-1 ) (ω1 , 0 ) (ω2 , 0 ) (ω3 , 0 ) (ω0 , 0 ) (ωр , 0 ) (ωж , 01 1,00 -87,75 -2,01 -1,15 -90,91 -84,33 -175,24 2 5,00 -78,73 -9,93 -5,74 -94,40 -63,47 -157,87 3 10,00 -68,23 -19,30 -11,54 -99,07 -45,02 -144,09

---

4 15,70 -57,90 -28,80 -18,32 -105,02 -32,51 -137,53 5 30,00 -39,83 -46,42 -37,60 -123,85 -18,44 -142,29 6 50,00 -26,58 -60,29 -88,26 -175,12 -11,32 -186,44 7 71,40 -19,31 -68,23 -90,00 -177,53 -7,98 -185,51 8 100,00 -14,04 -74,09 -113,90 -202,03 -5,71 -207,75 9 150,00 -9,47 -79,26 -159,00 -247,73 -3,82 -251,54 10 270,00 -5,29 -84,00 -174,01 -263,31 -2,12 -265,43 11 500,00 -2,86 -86,77 -178,24 -267,88 -1,15 -269,03 12 1000,00 -1,43 -88,41 -179,55 -269,39 -0,57 -269,97 ЛАЧХ и ЛФЧХ объекта регулирования представлены на рис. 5. 1.3 Построение желаемой частотной характеристики разомкнутой системы и синтез корректирующего устройства:Среднечастотная часть характеристики с наклоном -20 дБ/дек имеет частотный диапазон в пределах íω <ω< вω и составляет около одной декады. Данный диапазон включает частоту среза сω и определяет показатели качества замкнутой системы. Частота среза желаемой ЛАЧХ разомкнутой системы определяется по формуле: 1mсс7,51 0,2 3,14 t π ω −=== Граница первой низкочастотной области вычисляется по заданным показателям качества и имеет вид: 1mп1нс10 0,20,4 2 tt 2 ω −= − = − = Низкочастотная часть желаемой ЛАЧХ обуславливает точность воспроизведения управляющего воздействия. Форма характеристики в этом диапазоне ( )11н10сω;0ω −= зависит от требуемого порядка астатизма. Высокочастотная часть характеристики с наклоном -60 дБ/дек находится в пределах ( )= −;0,100 11св и не оказывает существенного влияния на показатели качества системы, поэтому формы желаемой характеристики и ЛАЧХ неизменяемой части совпадают. ЛАЧХ последовательного корректирующего устройства находится как разность желаемой ЛАЧХ и ЛАЧХ неизменной части, затем определяем передаточную функцию регулятора )(pWрс. Желаемая ЛАЧХ и ЛФЧХ разомкнутой системы представлены на Передаточная функция регулятора скорости имеет вид: p 10,1p 89,125 p 1pT K(p)W рс рсрс + = + = ,где с1,0 10 1 ω 1 T1нрс=== . 22TlgK20 рсрс= => 89,125 0.1 10 T 10 K 20 22рс 20 22рс=== Передаточная функция желаемой ЛАЧХ имеет вид:

---

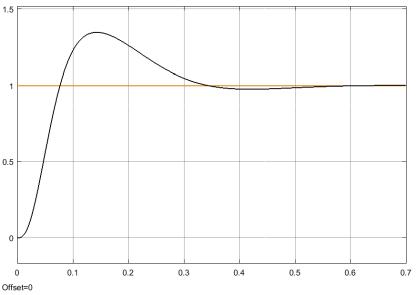
1714,0014,02014,0 1 1035,0 1)104,0(302,1 p10,1p89,125(p)W(p)W(p)W 22НЧРСЖ++  +  + +== ppppp1.4 Анализ качества по реакции на ступенчатое управляющее воздействие:С помощью моделирующего комплекса Simulink оцениваем показатели качества полученной системы при )(1)( ttз= и 0)( =tiс: 1) перерегулирование( )%50;30%8,34σ = , 2) время достижения максимума( ) с0,2;0,15с0,146t m= , 3) время переходного процесса( ) с0,4;0,30,3сt п= . Спроектированная система обеспечивает заданные показатели качества переходного процесса, изображенного на рис. 7. 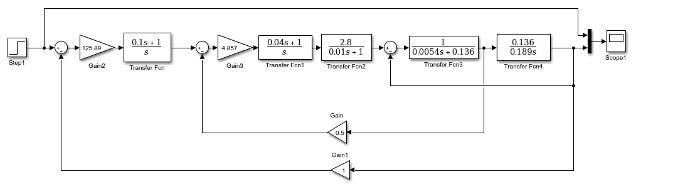Рис. 7. Реакция системы регулирования скорости ω(t) при 1(t)ωç= и 0N(t)0,(t)iñ== Рис. 6. Реакция системы регулирования скорости ω(t) при 1(t)ωç= и 0N(t)0,(t)iñ== 2. Исследование устойчивости и качества системы2.1 Определение запасов устойчивости:Оцениваем устойчивость системы по желаемым ЛАЧХ и ЛФЧХ: дБ 613,2д3ΔL = -запас устойчивости по амплитуде, 0O305,43Δ = - запас устойчивости по фазе. Запасы устойчивости удовлетворяют заданным показателям. 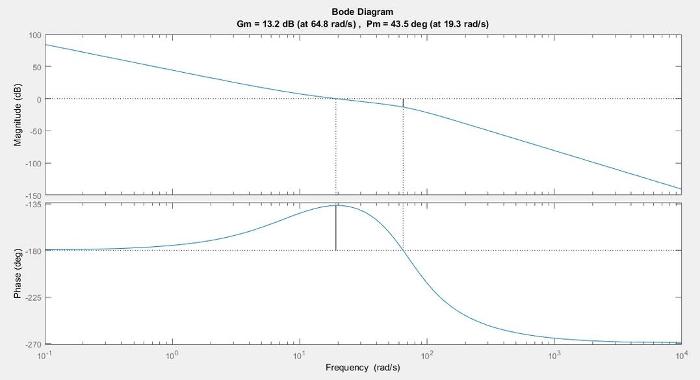Рис. 8. Запас устойчивости по амплитуде и запас устойчивости по фазе 2.2 Построение реакции системыω(t) ,i(t) на возмущающее воздействие -ступенчатое изменение1(t)(t)iс= :С помощью моделирующего комплекса ‘MatLab’ вычисляем реакцию замкнутой системы регулирования скорости ω(t) , i(t) при единичном возмущающем воздействии 1(t)(t)iс

---

= . Управляющее воздействие при этом полагается равным нулю 0(t)ωз= .




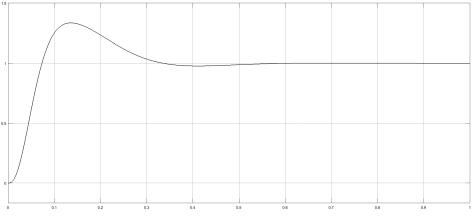
Рис. 9. Структурная схема САУ в Simulink при 1(t)(t)iс= и 0(t)ωз=




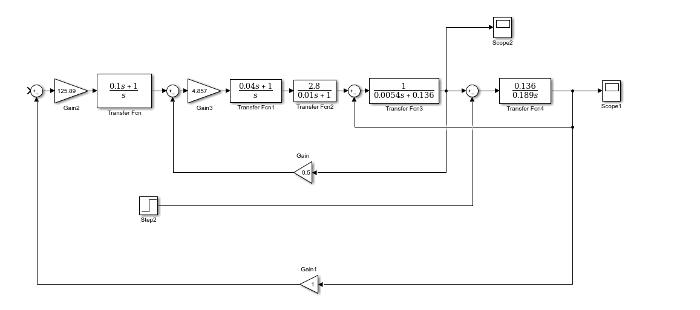
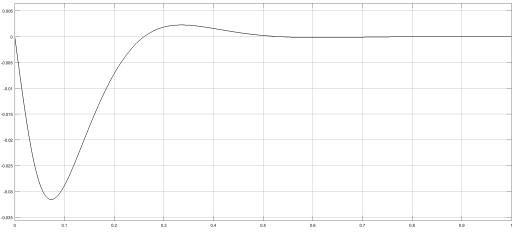
Рис. 10 Реакция тока i (t) , при 1(t)(t)iс= и 0N(t)0,(t)ωз== Рис. 11 Реакция скорости ω(t) , при 1(t)(t)iс= и 0N(t)0,(t)ωз==




воздействие:




С помощью моделирующего комплекса MatLab вычисляем реакцию замкнутой системы регулирования скорости ω(t) ,i(t) при трапецеидальном законе изменения

задающего воздействия (t)ωзс временами разгона, торможения и работы на

установившейся скорости по с1,5 и значением установившейся скорости, равном 1.

Возмущающее воздействие при этом полагается равным нулю 0(t)iс= . Его график

представлен на рис. 12.

При разгоне и торможении возникают переходные процессы, которые очень быстро

затухают, а величина установившейся ошибки принимает значение 0ε уст= . Поскольку

трапецеидальное воздействие было реализовано при помощи линейных элементов, система отрабатывает ее без ошибки, а это свидетельствует о втором или большем порядке астатизма. Полученный результат удовлетворяет требуемому условию.




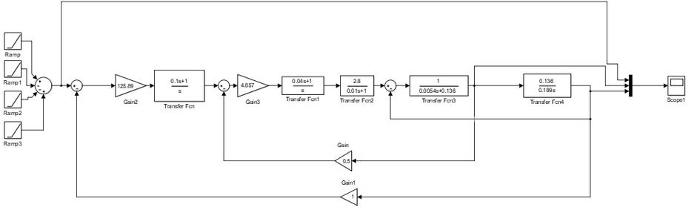
Рис. 12. Структурная схема САУ в Simulink при трапецеидальном воздействии и

0N(t)0,(t)iс==

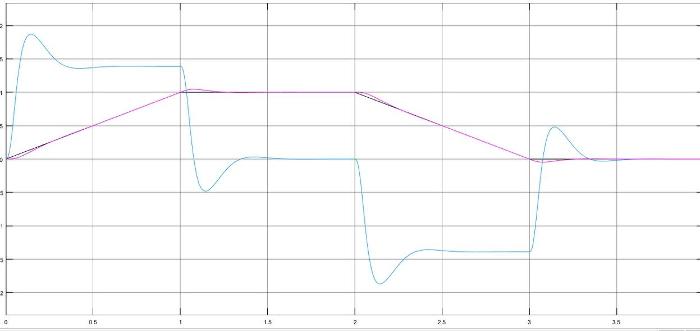
Рис. 13. Реакция системы регулирования скорости ω(t) и тока i(t) при трапецеидальном

воздействии и 0N(t)0,(t)iс==

3. Исследование точности системы

3.1 Вычисление коэффициентов ошибок и систематических ошибок:

1714,0014,02014,0

1

1035,0

1)104,0(302,1

p

10,1p

89,125(p)W(p)W(p)W

22НЧРСЖ++



+




+




+

==

pppp

p

=

+++

++

==


−− 234557


2


1045,000577,01045,91056,7

---

Смотрите также файлы

• Вопросы к экзамену по предметам Фармакология.docx

• Производство заготовок.ppt

• Практических заданий по дисциплине экономика развития.docx

• Инструментальные материалы.ppt

• Группа 21М511в.docx