Файл: Расчет системы регулирования скорости электропривода.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 95
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
12104,1739695,206848,0
)()()(
pppp
pp
pWpWpWНЧРСЖ
Для оценки точности системы используется передаточная функция системы по ошибке
)( pG, которая определяется по структурной схеме замкнутой системы:
)(
)(
12104,1739695,217298,000577,01045,91056,77
1045,000577,01045,91056,7
)(1
1
)(
234557
234557
PX
pE
ppppp
pppp
pW
pG
Ж
=
+++++
+++
=
=
+
=
−−
−−
По методу деления полиномов числителя и знаменателя имеем:
57
1056,77
45
1045,9
3
00577,0
2
17298,039695,212104,17
57
1056,7
45
1045,9
3
00577,0
2
1045,0 ppppppppp
−
+
−
++++⊥
−
+
−
++
...21045,0 p ...
23
101,6 p
−
+0
Выражение для ошибки )()()( pXpGpE= при разложении )( pG в ряд
МакЛорена, сходящийся при малых значениях 0→p (т.е. →t), имеет вид:
+++=
=+++++=
=
+++++=
−)(105)(0)(0
)(
!
)(
!3
)(
!2
)()(
!
)0(
!3
)0(
!2
)0(
)0()0()()(
23
3
3
2
210
)(
3
///
2
//
/
pXpppXpX
pX
n
p
cpX
p
cpX
p
cppXcpXc
p
n
G
p
G
p
G
pGGpXpE
n
n
n
n
Откуда имеем 3
3
210;101,6!2;0;0 сссс
−=== - коэффициенты ошибок системы
регулирования, по которым можно оценить величину систематической установившейся ошибки при различных входных воздействиях )(tx:
+++=
=+++++=
−
2
2
3
3
3
3
2
2
2
10
)(
105
)(
0)(0
)(
!
)(
!3
)(
!2
)(
)()(
dt
txd
dt
tdx
tx
dt
txd
n
c
dt
txdc
dt
txdc
dt
tdx
ctxcp
n
n
n
Значения установившихся ошибок:
При единичном ступенчатом задающем воздействии 1(t)(t)ωз=
1(t))( =tx; 0
)(
=
dt
tdx
01(t)01(t)0=== cуст
При линейно нарастающем задающем воздействии 1(t)t(t)ωз=
1(t)t)( =tx; 1
)(
=
dt
tdx
; 0
)(
2
2
=
dt
txd
0101(t)t0
)(
1(t)t 10=+=+=
dt
tdx
ccуст
При параболическом задающем воздействии 1(t)t(t)ω
2
з=
1(t)t)( 2=tx; t2
)(
=
dt
tdx
; 2
)(
2
2
=
dt
txd
; 0
)(
3
3
=
dt
txd
0122,0101,62t201(t)t0
)(
!2
)(
1(t)t 32
2
2
2
1
2
0=++=++=
−
dt
txdc
dt
tdx
ccуст
3.2 Оценка степени влияния помех Используя ЛАЧХ на рис. 5, рассмотрим влияние помехи на замкнутые контуры регулирования скорости и тока. Для этого определим амплитуды пульсации ω(t) и i(t) ,
обусловленные регулярной помехой tsinωaN(t) NN= , где
1
NNс40ω;0,01a
−== ,
приложенной к входу системы.
По рис. 5: рωрωNрωlgA20(120)L)(ωL ==
4467,0A
10A
lgA207-
рω
20
7
рω
рω
=
=
=
−
0
рωNрω152(40))(ω −== ;
( )
0,697
1152cos0,446720,4467
0,4467
1)(ωcos)(ω2A)(ωA
)(ωA
)(ωA
02
NрωNрωN
2
рω
Nрω
Nзω=
+−+
=
++
=
Амплитуда пульсации скорости:
-3
NзωNω1097,6697,00,01)(ωAaa === . Определим амплитуду пульсации тока: p 0,72
pT ρ (p)W М Д2== ;
018,0
40
72,0
ω189,0
0,136
)(ωW)(ωA
N NД2NД2==
==
72,38
018,0
0,697
)(ωA )(ωA )(ωA NД2 Nзω Nзi===
Амплитуда пульсации тока: 0,387272,380,01)(ωAaa NзiNi=== 3.3 Оценка ошибок системы моделированием
а) Результаты, полученные в пункте 3.1, проверяем моделированием в приложении
15), линейно нарастающее t(t)ωз= (рис. 17) и параболическое
2
зt(t)ω = (рис. 19) задающие воздействия и измеряем величину установившейся ошибки.
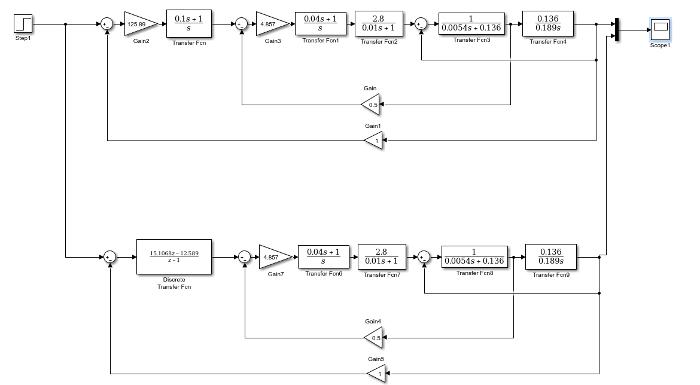
Рис. 14. Структурная схема САУ в Simulink при ступенчатом задающем воздействии
1(t)(t)ωз=
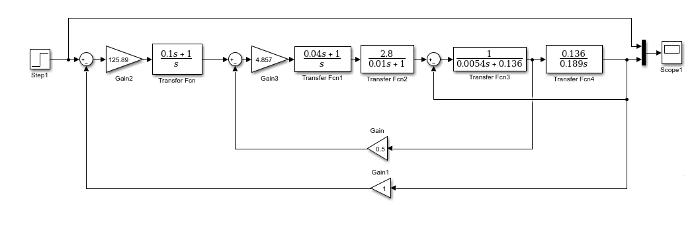
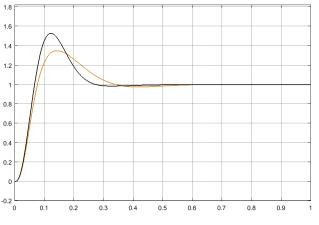
Рис. 15. Реакция системы на ступенчатое задающее воздействие 1(t)(t)ωз=
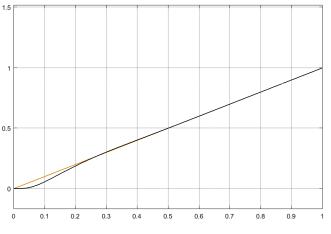
Рис. 17. Реакция системы на линейно нарастающее задающее воздействие t(t)ωз=
Рис. 18. Структурная схема САУ в Simulink при параболическом задающем воздействии
2
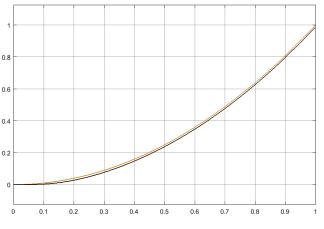
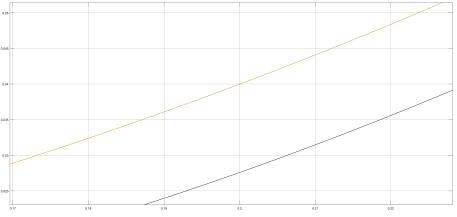
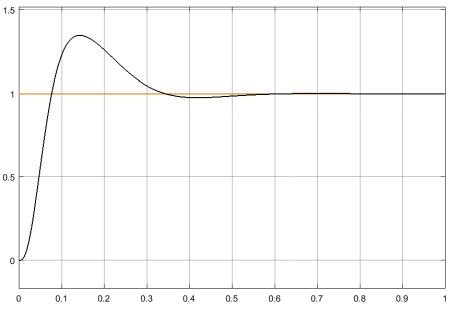
уст =0,0122 Рис. 19. Реакция системы на параболическое задающее воздействие
2
çt(t)ω =
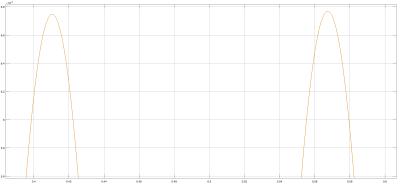
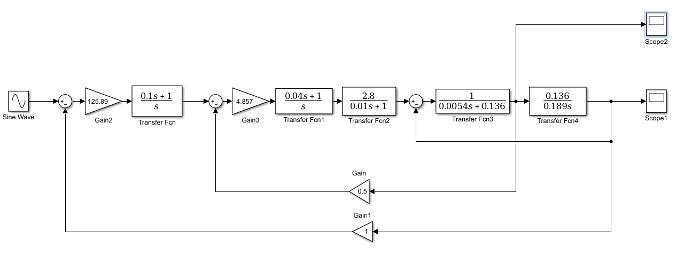
б)Результаты, полученные в пункте 3.2, проверяем моделированием в приложении
Simulink. Для оценки степени влияния помех на вход системы подается помеха
tsinωaN(t) NN= и измеряются установившиеся амплитуды скорости ω (рис. 21) и тока i
(рис. 22).
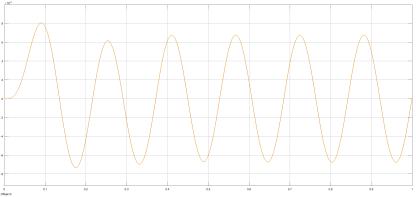
Рис. 20. Структурная схема САУ в Simulink при влиянии помех на вход системы
tsinωaN(t) NN=
3
NN1077,6at sinωaN(t)
−==
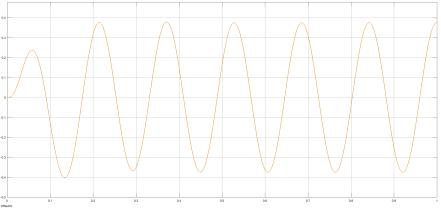
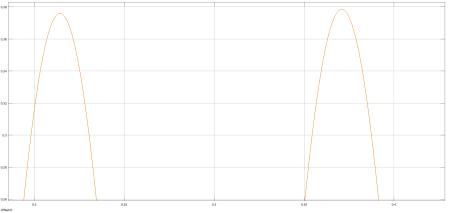
Рис. 22. Величина установившийся амплитуды тока i при влиянии помехи
375,0at sinωaN(t)
iNN==
4. Конструктивные расчеты регулятора скорости
4.1 Определение параметров непрерывного регулятора скорости:
Принципиальная схема регулятора реализуется в виде активного фильтра, изображенного на рис. 23. Передаточная функция регулятора имеет вид:
p
10,1p
95,19
p
1Tp
K(p)WР С
+
=
+
=
Задаемся мкФ0,1С = и вычисляем:
кОм434,97
100,189,125
1
CK
1 R
61
=
=
=
−
;
МОм 1
100,1
0,1
C
T R
62
=
==
−
;
Ом2,38
R2R
RR
R
R
1
R
1
R
1
R
1
12
21
3
2113
к=
+
=
++=
Из стандартного ряда значений сопротивлений E96 , соответствующего резисторам с
допуском %1 , принимаем: кОм6,80R1, МОм1R 2= , Ом 3,38R3к= .
Рис. 23. Принципиальная схема регулятора
скорости
xос
xз
R3
R2
R1
R1
C
∞ 4.2 Расчет алгоритма работы цифрового регулятора:
Для перехода от передаточной функции аналогового регулятора скорости (p)Wрс к
соответствующей дискретной передаточной функции (z)Wрс выполним подстановку
Tz
1z p
− = , где c0,02T = - период дискретности по времени:
1z
0,1-0,12z
89,125
Tz
1z
1
Tz
1z
0,1
89,125(z)W
p
10,1p
89,125(p)W
рс
рс
−
=
−
+
−
=
+
=
Преобразуем полученную дискретную передаточную функцию (z)Wрс:
( ) ( )
(z)izε(z)z589,12ε(z)1068,15(z)i
(z)iz(z)iε(z)z589,12ε(z)1068,15
z1(z)iz589,121068,15ε(z)
ε(z)
(z)i
z1
z589,121068,15
(z)W
з
11 з
з
1
з
1
1
з
1
з
1
1
рс
+−=
−=−
−=−
=
−
−
=
−−
−−
−−
−
−
Перейдем к решетчатой функции 1z−= nT:
T)(nTi1T)ε(nT589,12ε(nT)1068,15(nT)i зз−+−−=
Итак, получили алгоритм работы цифрового регулятора в виде разностного уравнения общего вида:
+−+−++−+−+= 2T)(nTibT)(nTib2T)ε(nTaT)ε(nTaε(nT)a(nT)i
з2з1321з
Откуда 0...b,1b;0a;589,12a;1068,15a 11321===−== 4.3 Анализ качества системы с цифровым регулятором скорости при ступенчатом изменении управляющего воздействия1(t)(t)ωз= :
Построим переходный процесс в системе с цифровым регулятором при ступенчатом управляющем воздействии 1(t)ωз= в приложении Simulink: