ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 192
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Сверточный код.
Свёрточный код относится к классу непрерывных кодов. Сверточный кодер после формирования выходной комбинации, соответствующей входному информационному символу, не переходит в исходное начальное состояние, а кодирует следующий информационный символ, — начиная кодирование из того состояния, в котором он оказался после передачи предыдущего символа. Следовательно, между символами выходной кодированной последовательности существуют корреляционные связи,
позволяющие повысить помехоустойчивость декодирования. Кроме этого, сверточный кодер имеет не один, а п выходов, на каждом из которых формируется из одной и той же информационной последовательности своя собственная выходная последовательность в соответствии с порождающим полиномом, соответствующим данному выходу. Для рис n=2 и порождающие полиномы имеют вид: р1(Z)= (1+z2); P2(Z)=(1+Z+Z2). Сначала передаются первые импульсы с каждого из п выходов, потом вторые и т.д. Очевидно, что скорость передачи падает в n раз.
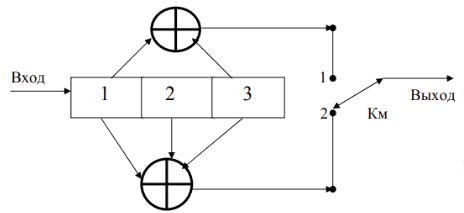
Сверточный код — частный случай решетчатых кодов. Решетчатая диаграмма на рис.5.4 для сверточного кода, формируемого кодером рис.5.3 - это один из способов задания сверточного кода. Каждое сечение соответствует внутреннему состоянию кодера; ребро соответствует передаваемому символу на входе: верхнее — 0; нижнее - 1. Около ребра написана комбинация из двух бит, которая появится на выходе, если на входе 1 или 0.
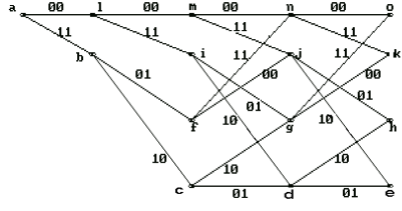
Пусть на вход кодера рис.5.3 поступила комбинация 101. Ей соответствует полином а(Z)=1+Z2. На первом выходе кодера получим b1(Z)=a(Z)*P1(Z)= (1+Z2)*(1+ Z2)=1+Z
4. Этот полином соответствует комбинации 10001. На втором выходе кодера получим b2(Z)=а(Z)*P2(Z)= (1+Z2)* (1+Z+Z2) =1+Z+Z3+Z4. Это соответствует комбинации 11011.Следует учесть, что сложение коэффициентов осуществляется по модулю 2, т.е.Z+Z=(1(+)1)Z=0. Совместим эти комбинации: сначала передается первый символ с первого выхода, потом первый символ со второго выхода, потом второй символ с первого выхода, потом второй символ со второго выхода и тд. Получим 110100...... Аналогичный результат получим с помощью решетчатой диаграммы: при передаче | идем по нижнему ребру и в канал связи передается 11, далее передается 0, идем по верхнему ребру и в канал передается 01, далее передается 1, а в канал идет 00 ит.д. Структурная схема декодера сверточного кода показана на рис. Декодирование сверточного кода осуществляется в соответствии со схемой. Пусть передавали 110100...., приняли 100100...Ошибка во 2-ом символе. Покажем, как декодер исправляет эту ошибку.
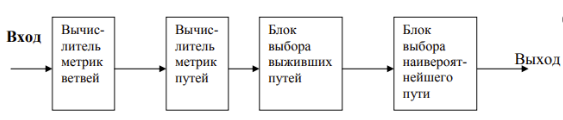Декодирование осуществляется поэтапно путем анализа очередных n бит (метрики ветвей). Для рассматриваемого кодера n=2. Приняли первые два бита 0. Кодовое расстояние между 10 и путем аl, которому соответствует 00, равно d=1(метрика ветви аl). Кодовое расстояние между 10 и путем ab, которому соответствует 11, равно d=1 (метрика ветви аb). Сохраняем оба пути. Приняли следующие два бита 01. МетрикиБилет 16
1. Амплитудный модулятор. СМХ. (Сам модулятор в 38)
СМХ –это зависимость амплитуды 1-ой гармоники выходного тока I1 модулятора от напряжения смещения E при амплитуде вч несущей Um=const и амплитуде нч модулирующего сигнала Vm = 0.
2. Дифференциальная энтропия. Взаимная информация.
Теорема Шеннона
(выше)
Билет 17
1 Частотная модуляция. Формула, временные и спектральные диаграммы.
При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.
чм (t) = 0 + Uнч(t), где (9.1)
чм (t)- частота ЧМ сигнала;
0- среднее значение несущей частоты;
Uнч(t)-модулирующий сигнал;
-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.
Если модулирующий сигнал гармонический, т.е.
Uнч = cost,
то чм(t) = 0 + соst
а выражение для ЧМ сигнала имеет вид:
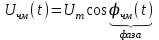
чм(t) =
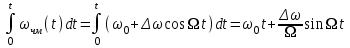
Uчм(t) = Umcos(0t+
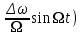
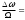Mч - индекс ЧМ. (9.2)Uчм(t) = Umcos(0t+
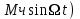
Временная диаграмма модулирующего сигнала имеет вид:
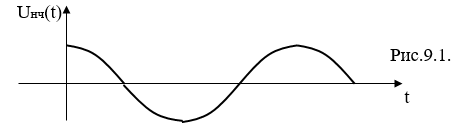
Временная диаграмма соответствующего ЧМ сигнала принимает вид:
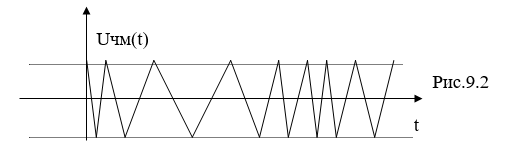
Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше , а период колебаний меньше.
чм(t) = 0 + cost
max = 0 +
min = 0 -
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
Uчм(t) = Umcos(0t+
= Um0(Mч)cos0t+ Um1(Mч)cos(0+)t- Um1(Mч)cos(0)t+Um2(Mч)cos(0+2)t+Um2(Mч)cos(02)t+Um3(Mч)*cos(0+3)t- Um3(Mч)cos(0-3)t+k(Mч) - функция Бесселя к-ого порядка.
Вид спектра зависит от Мч.
Спектр ЧМ сигнала при Мч<<1 (т.е. порядка 0,1; 0,05;)
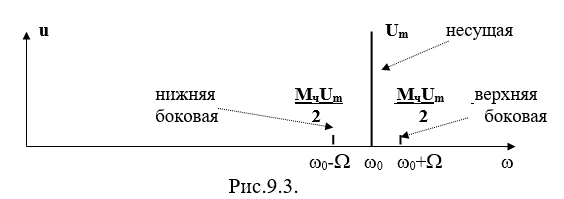
При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых ), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.
Спектр ЧМ сигнала при Мч>1 выглядит так (Мч=5):
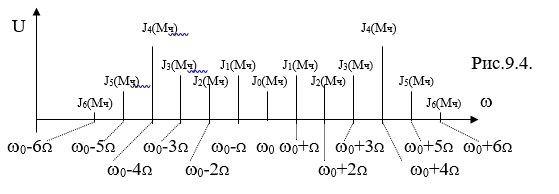
Полоса частот сигнала ЧМ.
Пчм 2(Мч+1)
Мч<<1 Пчм 2, ( как при АМ )
Мч>>1 Пчм 2Мч = 21>1>1>
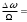2Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.
2. Согласованный фильтр (выше)
Билет 18
1.Теорема Котельникова. АИМ.
Теорема Котельникова: любая непрерывная функция х(t), спектр
к
оторой ограничен частотой ωв=2πfв, полностью определяется своими отсчетами, взятыми через интервал времени
АИМ- амплитудно-импульсная модуляция,
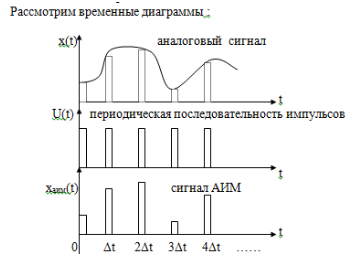
АИМ сигнал можно записать в виде:
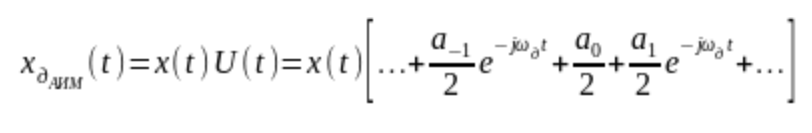
В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности.
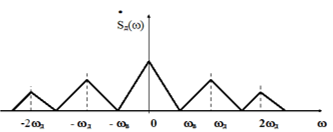
Спектр АИМ сигнала, следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта - импульсами , но амплитуда составляющих спектра убывает с ростом номера гармоники :
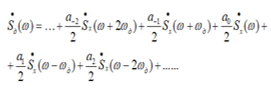
Спектр АИМ сигнала принимает вид:
2.ШПС.
Одна из трудноразрешимых проблем при разработке новых систем связи – проблема нахождения оптимальных систем сигналов, реализующих максимальные скорость передачи и помехоустойчивость приема. Для многолучевых каналов мобильной связи устойчивую связь можно получить, в частности, используя сложные, шумоподобные сигналы. К таким сигналам относятся М-последовательности, коды Баркера, функции Уолша и т.п. Сложные или шумоподобные сигналы называют также псевдослучайными последовательностями (ПСП). Псевдослучайная последовательность - это последовательность 1 и -1, которые генерируются по определенным известным правилам, но внешне напоминают реализацию шума. По этой причине такие последовательноси называются также шумоподобными.
Для ПСП характерно также, что их база В, т.е. произведение длительности сигнала Т на ширину его спектра F значительно больше 1: B=FT>> 1. (3.16) Поэтому ПСП называют также сигналами с большой базой. ПСП выбирают так, чтобы их автокорреляционная функция имела явно выраженный максимум, а взаимокорреляционная функция была близка к нулю.