ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 186
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 элемента, если всего произведено 12 независимых опытов.
5. Автомат штампует детали. Контролируемая длина детали распределена по нормальному закону с проектной длиной, равной 40 мм. Длины фактически изготовленных деталей находятся в пределах от 34 мм до 46 мм. Найти вероятность того, что длина наудачу взятой детали окажется не более 41 мм.
Вариант 23
1. Два самолета, независимо один от другого, производят стрельбу по воздушной мишени, делая по два одиночных выстрела. Вероятность попадания при каждом выстреле для первого самолета равна 0,7, а для второго – 0,4. Построить ряд и функцию распределения случайной величины X – числа попаданий обоих самолетов в цель.
2. При некотором технологическом процессе станок-автомат производит 50 % изделий высшего сорта, 30 % – первого сорта и 20 % - второго сорта. Построить ряд распределения и найти дисперсию случайной величины X – числа первосортных изделий среди 3 отобранных.
3. Случайная величина X может принимать любое положительное значение. Определить ее математическое ожидание и среднеквадратическое отклонение, если плотность распределения имеет вид:
.
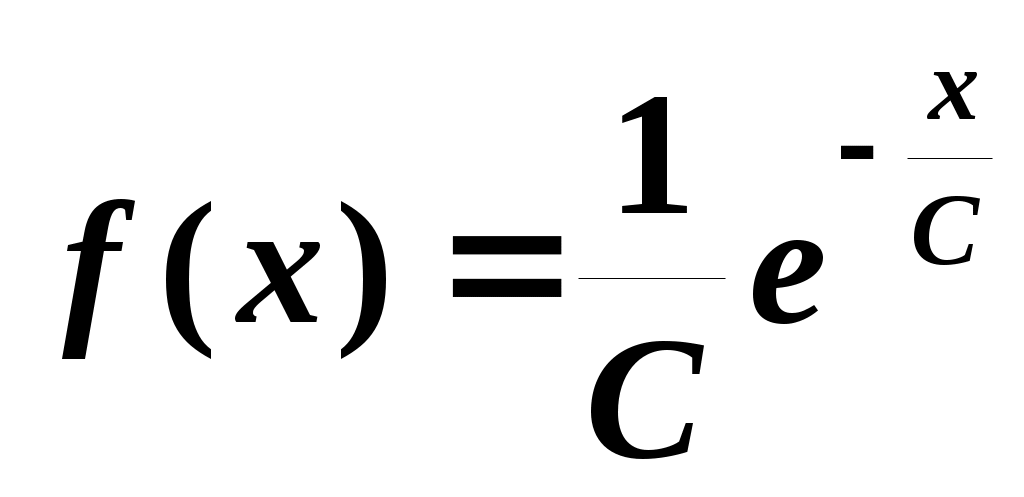4. Найти дисперсию дискретной случайной величины X – числа появления события A в 20 независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и математическое ожидание M(X) равно 0,7.
5. Станок-автомат изготовляет ролики, контролируя их диаметр, распределенный по нормальному закону с математическим ожиданием 8 мм и стандартным отклонением 0,2 мм. Найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,9 заключены диаметры изготовленных роликов.
Вариант 24
1. Стрелок ведет стрельбу по мишени до первого попадания в мишень, имея боезапас 4 патрона. Вероятность попадания в мишень при каждом выстреле равна 0,6. Построить ряд и функцию распределения случайной величины X – числа израсходованных патронов.
2. В партии из 14 изделий, среди которых 4 бракованных, наудачу выбраны 3. Написать ряд распределения случайной величины
X – отношения числа стандартных изделий к числу бракованных среди отобранных изделий.
3. Функция распределения случайной величины X имеет вид:
.
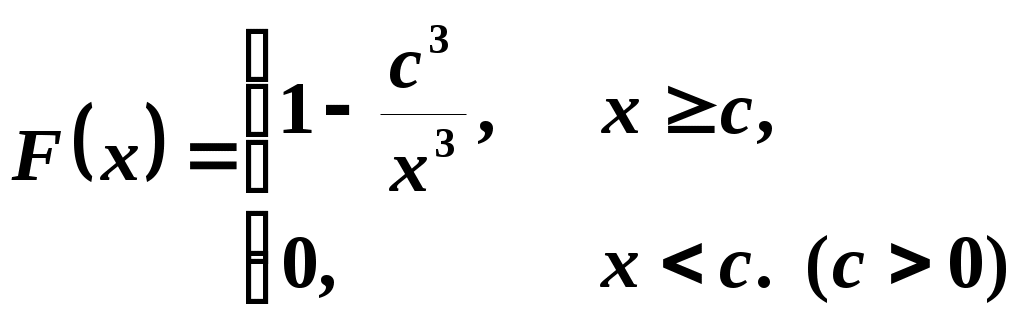Определить математическое ожидание и среднее квадратическое отклонение этой случайной величины.
4. Устройство состоит из 3 элементов. Вероятность отказа любого элемента за время опыта равна 0,3. Найти дисперсию числа таких опытов, в каждом из которых откажет ровно 2 элемента, если всего произведено 8 независимых опытов.
5. Высотомер измеряет высоту с ошибкой, починенной нормальному закону со средним квадратическим отклонением 70 м. Систематическая ошибка равна 40 м. Найти вероятность того, что измерение высоты не выйдет из пределов 80 м.
Вариант 25
1. Цель атакуют три вертолета. Вероятности попадания в цель для каждого из них соответственно равны 0,8, 0,3 и 0,4. Первый и второй вертолеты производят по цели по одному выстрелу, а третий – два. Построить ряд распределения и функцию распределения случайной величины X – числа попаданий в цель.
2. Стрелок, имеющий 3 патрона, стреляет по мишени до первого попадания или пока не израсходует все патроны. Вероятность попадания при одном выстреле 0,6. Построить ряд распределения и найти дисперсию случайной величиныХ – числа израсходованных патронов.
3. Дифференциальная функция распределения времени безотказной работы аппаратуры имеет вид: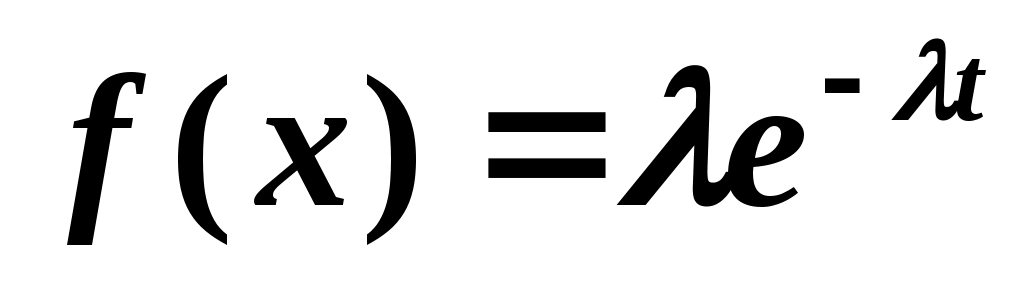
. Определить математическое ожидание и среднее квадратическое отклонение времени безотказной работы аппаратуры.
4. Найти дисперсию дискретной случайной величины X – числа таких бросаний 3 игральных костей, в каждом их которых на двух костях появится по четыре очка. Общее число бросаний равно 10.
5. Систематическая ошибка удержания высоты самолетом +15 м. Случайная ошибка имеет среднеквадратическое отклонение 65 м. Для полета самолета отведен коридор высотой 100 м. Найти вероятность того, что самолет будет лететь ниже этого коридора, если самолету задана высота, соответствующая середине коридора.
Задания по теме “Математическая статистика”
Вариант 1
1. Найти эмпирическую функцию распределения по данному распределению выборки:
и изобразить её графически.
2. Найти выборочную среднюю и выборочную дисперсию по данному распределению выборки
3. Из большой партии деталей взяли на контроль веса по одной детали из каждого ящика. Требуется оценить вероятность того, что вычисленный по данным выборки средний вес детали отличается от среднего веса деталей во всей партии не более чем на 2 г., если известно, что s=5. Предполагается, что вес деталей распределен нормально.
4. Двумя приборами зафиксированы значения некоторой целочисленной величины. Получены результаты:
Можно ли считать, что приборы обладают одинаковой точностью, если принять уровень значимости a= 0,1. Предполагается, что выборки независимы, а результаты распределены нормально. (При проверке гипотезы о равенстве дисперсий в качестве конкурирующей принять гипотезу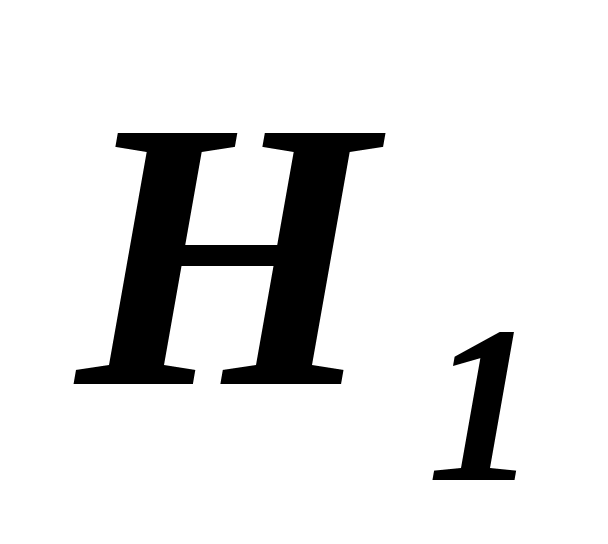
: D(X)¹D(Y)).
Вариант 2
1. Найти эмпирическую функцию распределения по данному распределению выборки.
2. Пользуясь данными интервальной выборки, определить выборочную среднюю и выборочную дисперсию
3. По выборке из большой партии изделий (n=100) оценить вероятность того, что средняя длина изделий, вычисленная по данным выборки, отличается от средней длины изделий всей партии не более чем на 0,4 мм, если известно, что s=0,9 мм. Предполагается, что длины изделий распределены нормально.
4. По выборке объема 66, извлеченной из нормальной двухмерной генеральной совокупности (X,Y), найден выборочный коэффициент корреляции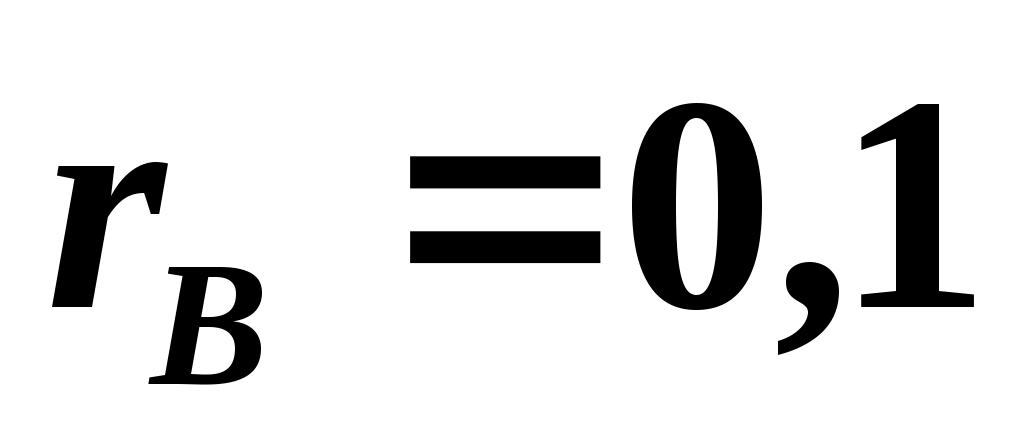
. Требуется при уровне значимости
0,05 проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
: 
.
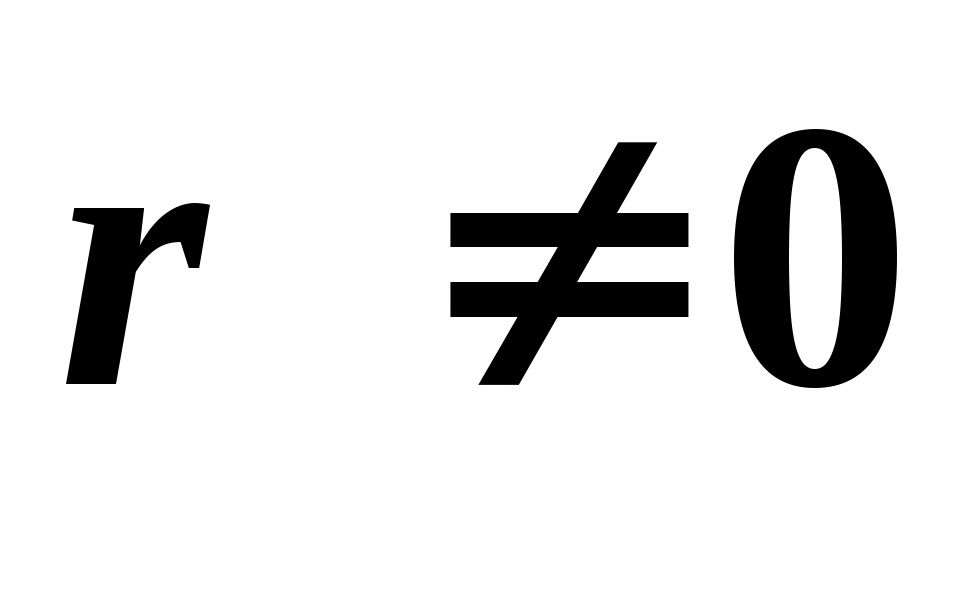Вариант 3
1. Построить гистограмму относительных частот по данному распределению выборки:
2. В результате десяти измерений прибором некоторой целочисленной величины получены следующие данные: 10; 11; 9; 7; 10; 8; 10; 7; 8; 10. Найти:1) выборочную среднюю результатов измерений; 2) выборочную дисперсию ошибок прибора.
3. Урожайность зерновых, исследованная на 400 выборочных гектарах, составила в среднем 20 ц. с гектара. Определить вероятность того, что средняя урожайность по краю отличается от средней выборочной не более, чем на 20%, если выборочная дисперсия равна 9 (выборка повторная).
4. По выборке объема 42, извлеченной из нормальной двухмерной генеральной совокупности (X,Y) найден выборочный коэффициент корреляции 0,2. Требуется проверить, значимо ли коэффициент корреляции отличается от нуля (при уровне значимости 0,01).
Вариант 4
1. Построить эмпирическую функцию распределения по данному распределению выборки:
5. Автомат штампует детали. Контролируемая длина детали распределена по нормальному закону с проектной длиной, равной 40 мм. Длины фактически изготовленных деталей находятся в пределах от 34 мм до 46 мм. Найти вероятность того, что длина наудачу взятой детали окажется не более 41 мм.
Вариант 23
1. Два самолета, независимо один от другого, производят стрельбу по воздушной мишени, делая по два одиночных выстрела. Вероятность попадания при каждом выстреле для первого самолета равна 0,7, а для второго – 0,4. Построить ряд и функцию распределения случайной величины X – числа попаданий обоих самолетов в цель.
2. При некотором технологическом процессе станок-автомат производит 50 % изделий высшего сорта, 30 % – первого сорта и 20 % - второго сорта. Построить ряд распределения и найти дисперсию случайной величины X – числа первосортных изделий среди 3 отобранных.
3. Случайная величина X может принимать любое положительное значение. Определить ее математическое ожидание и среднеквадратическое отклонение, если плотность распределения имеет вид:
.4. Найти дисперсию дискретной случайной величины X – числа появления события A в 20 независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и математическое ожидание M(X) равно 0,7.
5. Станок-автомат изготовляет ролики, контролируя их диаметр, распределенный по нормальному закону с математическим ожиданием 8 мм и стандартным отклонением 0,2 мм. Найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,9 заключены диаметры изготовленных роликов.
Вариант 24
1. Стрелок ведет стрельбу по мишени до первого попадания в мишень, имея боезапас 4 патрона. Вероятность попадания в мишень при каждом выстреле равна 0,6. Построить ряд и функцию распределения случайной величины X – числа израсходованных патронов.
2. В партии из 14 изделий, среди которых 4 бракованных, наудачу выбраны 3. Написать ряд распределения случайной величины
X – отношения числа стандартных изделий к числу бракованных среди отобранных изделий.
3. Функция распределения случайной величины X имеет вид:
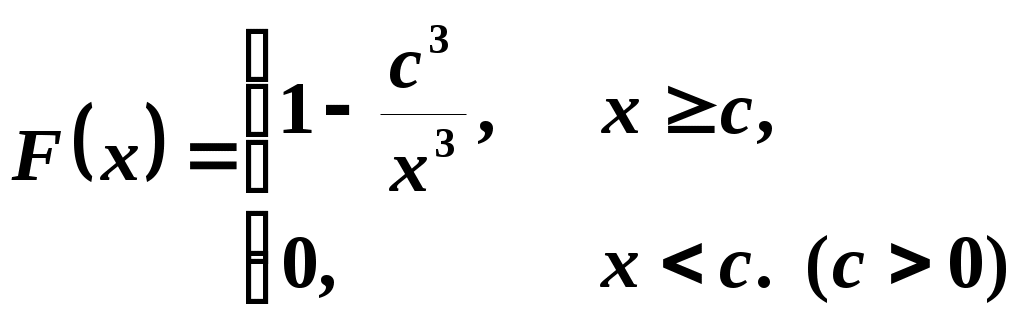.Определить математическое ожидание и среднее квадратическое отклонение этой случайной величины.
4. Устройство состоит из 3 элементов. Вероятность отказа любого элемента за время опыта равна 0,3. Найти дисперсию числа таких опытов, в каждом из которых откажет ровно 2 элемента, если всего произведено 8 независимых опытов.
5. Высотомер измеряет высоту с ошибкой, починенной нормальному закону со средним квадратическим отклонением 70 м. Систематическая ошибка равна 40 м. Найти вероятность того, что измерение высоты не выйдет из пределов 80 м.
Вариант 25
1. Цель атакуют три вертолета. Вероятности попадания в цель для каждого из них соответственно равны 0,8, 0,3 и 0,4. Первый и второй вертолеты производят по цели по одному выстрелу, а третий – два. Построить ряд распределения и функцию распределения случайной величины X – числа попаданий в цель.
2. Стрелок, имеющий 3 патрона, стреляет по мишени до первого попадания или пока не израсходует все патроны. Вероятность попадания при одном выстреле 0,6. Построить ряд распределения и найти дисперсию случайной величиныХ – числа израсходованных патронов.
3. Дифференциальная функция распределения времени безотказной работы аппаратуры имеет вид:
. Определить математическое ожидание и среднее квадратическое отклонение времени безотказной работы аппаратуры.4. Найти дисперсию дискретной случайной величины X – числа таких бросаний 3 игральных костей, в каждом их которых на двух костях появится по четыре очка. Общее число бросаний равно 10.
5. Систематическая ошибка удержания высоты самолетом +15 м. Случайная ошибка имеет среднеквадратическое отклонение 65 м. Для полета самолета отведен коридор высотой 100 м. Найти вероятность того, что самолет будет лететь ниже этого коридора, если самолету задана высота, соответствующая середине коридора.
Задания по теме “Математическая статистика”
Вариант 1
1. Найти эмпирическую функцию распределения по данному распределению выборки:
-
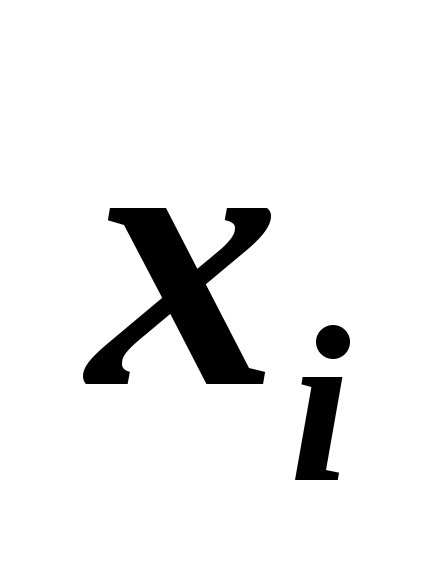
2
5
6
8
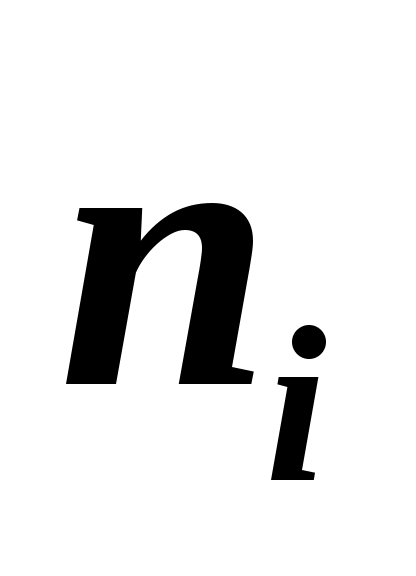
2
1
4
3
и изобразить её графически.
2. Найти выборочную среднюю и выборочную дисперсию по данному распределению выборки
-
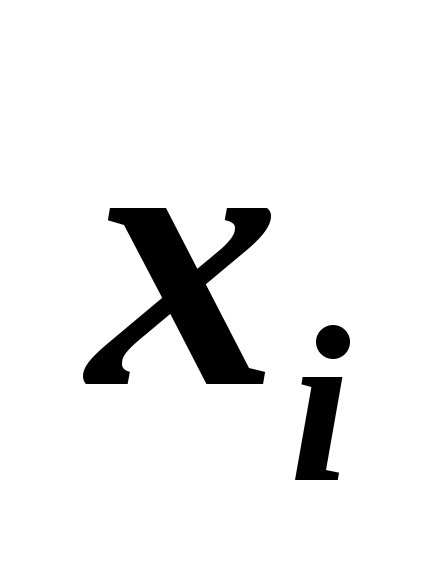
1,2
5,6
6
10
10,2
12
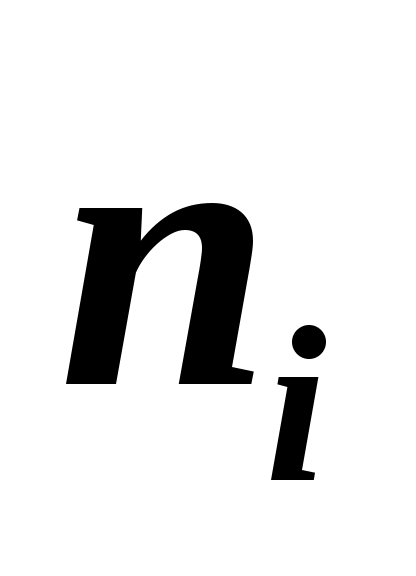
3
5
5
4
2
1
3. Из большой партии деталей взяли на контроль веса по одной детали из каждого ящика. Требуется оценить вероятность того, что вычисленный по данным выборки средний вес детали отличается от среднего веса деталей во всей партии не более чем на 2 г., если известно, что s=5. Предполагается, что вес деталей распределен нормально.
4. Двумя приборами зафиксированы значения некоторой целочисленной величины. Получены результаты:
-
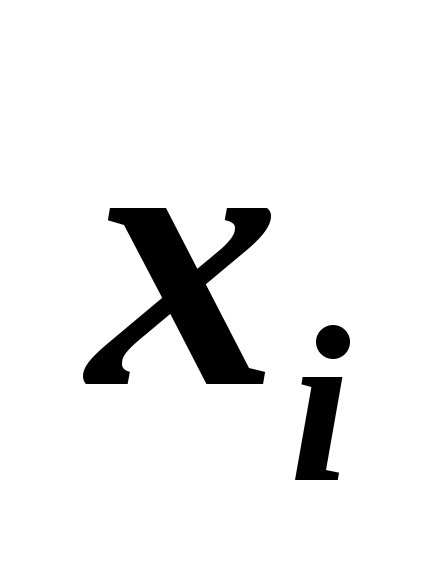
8
10
12
14
16
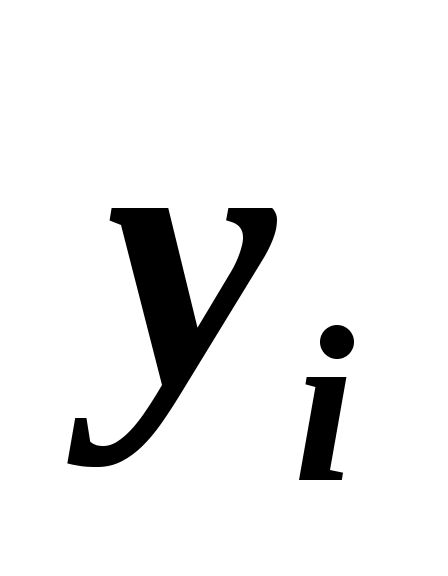
9
10
13
14
Можно ли считать, что приборы обладают одинаковой точностью, если принять уровень значимости a= 0,1. Предполагается, что выборки независимы, а результаты распределены нормально. (При проверке гипотезы о равенстве дисперсий в качестве конкурирующей принять гипотезу
: D(X)¹D(Y)).Вариант 2
1. Найти эмпирическую функцию распределения по данному распределению выборки.
-
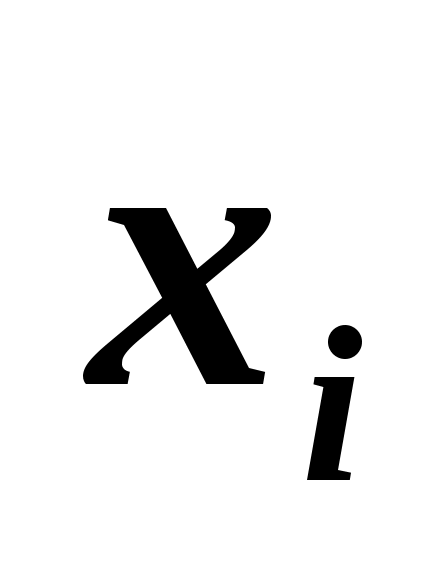
-2
7
9
10
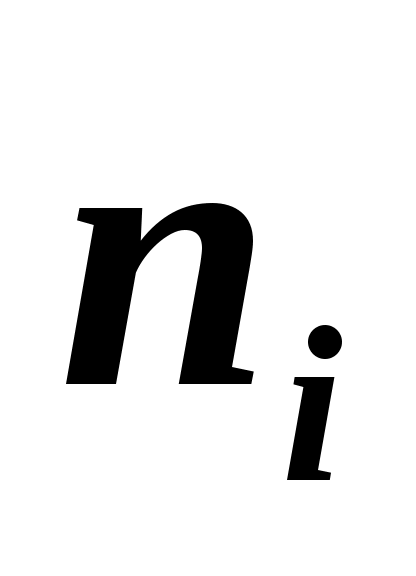
3
1
4
2
2. Пользуясь данными интервальной выборки, определить выборочную среднюю и выборочную дисперсию
-
-
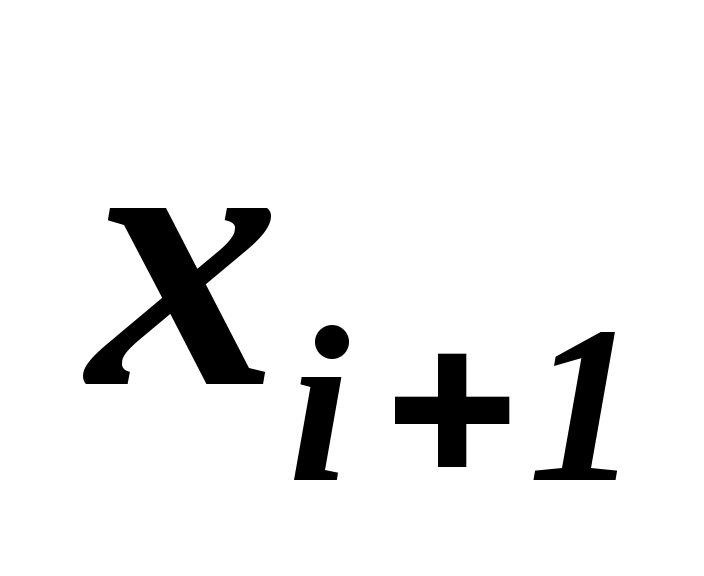
1-3
3-5
5-7
7-9
9-11
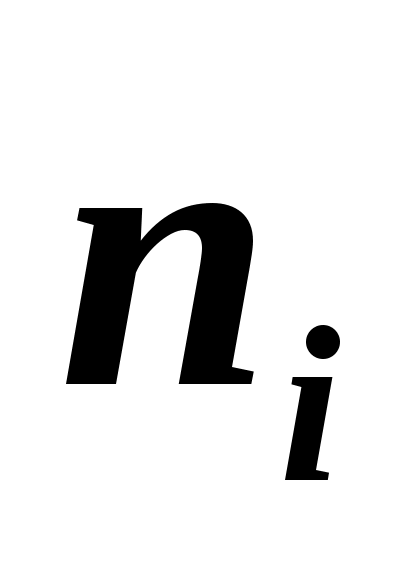
3
4
7
2
4
3. По выборке из большой партии изделий (n=100) оценить вероятность того, что средняя длина изделий, вычисленная по данным выборки, отличается от средней длины изделий всей партии не более чем на 0,4 мм, если известно, что s=0,9 мм. Предполагается, что длины изделий распределены нормально.
4. По выборке объема 66, извлеченной из нормальной двухмерной генеральной совокупности (X,Y), найден выборочный коэффициент корреляции
. Требуется при уровне значимости
0,05 проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
: .Вариант 3
1. Построить гистограмму относительных частот по данному распределению выборки:
- -
0-2
2-4
4-6
20
70
10
2. В результате десяти измерений прибором некоторой целочисленной величины получены следующие данные: 10; 11; 9; 7; 10; 8; 10; 7; 8; 10. Найти:1) выборочную среднюю результатов измерений; 2) выборочную дисперсию ошибок прибора.
3. Урожайность зерновых, исследованная на 400 выборочных гектарах, составила в среднем 20 ц. с гектара. Определить вероятность того, что средняя урожайность по краю отличается от средней выборочной не более, чем на 20%, если выборочная дисперсия равна 9 (выборка повторная).
4. По выборке объема 42, извлеченной из нормальной двухмерной генеральной совокупности (X,Y) найден выборочный коэффициент корреляции 0,2. Требуется проверить, значимо ли коэффициент корреляции отличается от нуля (при уровне значимости 0,01).
Вариант 4
1. Построить эмпирическую функцию распределения по данному распределению выборки:
-
1
3
5
7
10
5
20
15