ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 185
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. По выборке объема n=40 найти несмещенную оценку дисперсии генеральной совокупности, если
-
3
4
5
6
10
12
10
8
3. Для определения среднего роста новобранцев округа по схеме случайной бесповторной выборки обследованы 200 призывников. Найти вероятность того, что средний рост юношей в выборке отличается от среднего роста призывников округа не более чем на 2 см. (по абсолютной величине), если количество призывников в округе очень велико по сравнению с отобранными призывниками.
4. Двумя методами измерены значения некоторого количественного признака. Получены результаты:
-
2,3
2,7
2,1
3,0
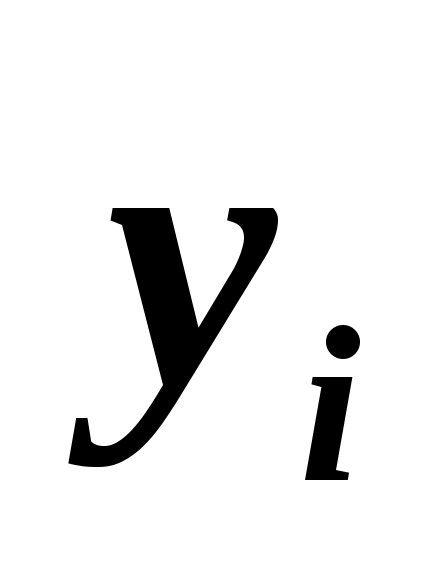
3,1
2,8
3,8
2,4
2,0
При уровне значимости a=0,1 проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипотезе
: D(X)¹D(Y). Сделать вывод о точности двух методов (можно ли считать её одинаковой или какой метод точнее).Вариант 5
1. По данной выборке: 1, 2, 3, 2, 4, 6, 1, 3, 2, 6 построить эмпирическую функцию распределения. Найти выборочную дисперсию по данному распределению выборки, перейдя к условным вариантам.
-
3500
3515
3520
3530
12
44
36
8
3. Результаты выборочной проверки 100 торговых точек из 1000 показали, что средняя выборочная цена определенного товара равна 25 руб. за кг., а выборочная дисперсия 36. Найти границы, в которых с вероятностью 0,99 заключена средняя цена данного товара во всех торговых точках, если выборка собственно случайная бесповторная.
4. В двух лабораториях проведены измерения одной и той же физической величины и получены следующие результаты
-
15,6
16
16,2
16,6
17
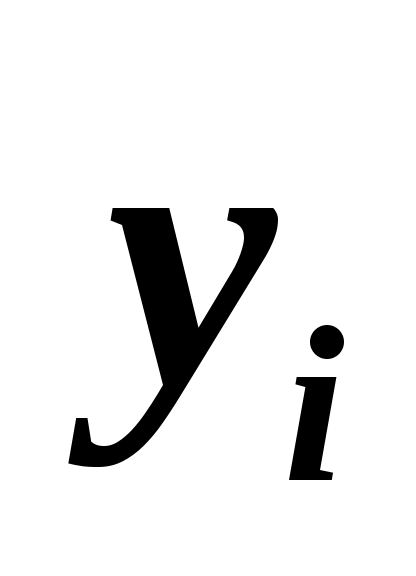
16,1
16,3
15,8
16,7
В предположении, что результаты измерений распределены нормально и выборки независимы, можно ли считать, что методики лабораторий обеспечивают одинаковую точность, если принять уровень значимости a=0,1.
Вариант 6
1. По данной выборке объема n=10: 8, 5, 6, 9, 10, 5, 9, 8, 6, 9; построить полигон относительных частот.
2. По данным взвешивания некоторого вещества одними весами (без систематических ошибок) получена выборка: 10, 11, 13, 14. Найти выборочную и исправленную дисперсии ошибок взвешивания.
3. По результатам измерения роста (в см.) случайно отобранных 100 студентов получено, что число студентов, рост которых не превышает 170 см., равно 74. Найти границы, в которых с вероятностью 0,95 заключена доля студентов во всем университете, рост которых не превышает 170 см. (предполагается, что случайная величина X – рост студентов распределена нормально.)
4. По выборке объема n=83 найден выборочный коэффициент корреляции
между двумя нормально распределенными случайными величинами X и Y. При уровне значимости 0,05 проверить, является ли значимой корреляционная связь между X и Y.Вариант 7
1. По данной выборке: 3, 5, 7, 6, 5, 3, 5, 7, 3; найти и построить эмпирическую функцию распределения.
2. Найти выборочную дисперсию по данному распределению выборки, перейдя к условным вариантам.
-
0,02
0,06
0,07
0,09
2
3
4
1
3. Взвешивание производили на весах, не имеющих систематической ошибки. Для выбранных 100 пачек чая из партии 10000 пачек чая средний вес составил 50,5 г. Найти с надежностью 0,95 точность оценки среднего веса пачек во всей партии
, зная, что среднее квадратичное отклонение s=2 мм. (Предполагается, что вес распределен нормально.)
4. Пять студентов были протестированы до и после тренинга по развитию памяти. Баллы, полученные каждым студентом до обучения (
) и после обучения (
), оказались следующими:-
35
38
43
50
47
40
39
42
50
49
Требуется при уровне значимости 0,05 установить, значимо или незначимо улучшилась способность к запоминанию студентов, в предположении, что число баллов распределено нормально.
Вариант 8
1. По данной выборке: 4, 7, 9, 11, 10, 4, 9, 10, 9, 7 построить полигон относительных частот.
2. По выборке объема 100 вычислена выборочная средняя и выборочная дисперсия диаметров валиков. Найти выборочную и исправленную дисперсии ошибок (точности заточки) станка, если диаметры валиков распределены нормально, а их дисперсия
.3. Найти минимальный объем выборки, при котором с надежностью 0,975 погрешность оценки среднего веса во всей партии по выборочной средней, меньше 0,5, если известно среднее квадратичное отклонение s = 2 г нормально распределенной генеральной совокупности.
4. Двумя методами определены значения одного числового параметра и получены следующие результаты:
-
10,5
12,6
13
13,8
11
11,7
12,5
13,5
14
В предположении, что результаты измерений распределены нормально и выборки независимы, можно ли считать, что методы обеспечивают одинаковую точность, если принять уровень значимости a = 0,05.
Вариант 9
1. Найти и построить эмпирическую функцию распределения по данному распределению выборки:
-
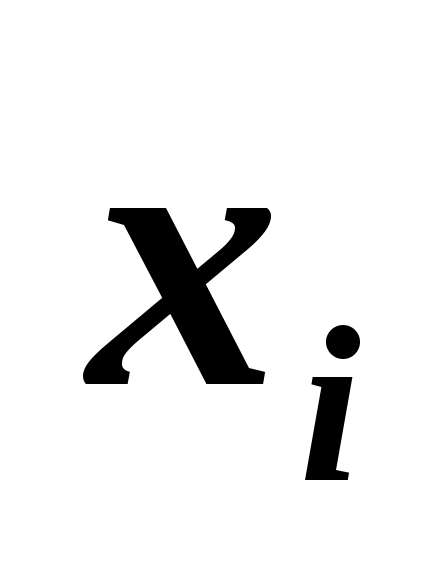
4
7
11
16
1
2
5
2
2. По выборке объема 101 найдены среднее выборочное
и среднее значение квадрата случайной величины 
. Найти несмещенную оценку дисперсии генеральной совокупности.3. В выборке объема n = 100 из большой партии изделий средний размер изделия оказался равным 34 см. Найти с надежностью 0,95 доверительный интервал для среднего размера изделий всей партии, если известно, что среднее квадратичное отклонение размера деталей в выборке равно 2,5. Предполагается, что размер изделия распределен нормально.
4. Двумя методами в одном и том же порядке определено содержание ртути в 6 пробах воды. Получены следующие результаты (в процентах в каждой пробе) при первом методе —
, при втором методе — 
-
0,05
0,03
0,01
0,04
0,06
0,05
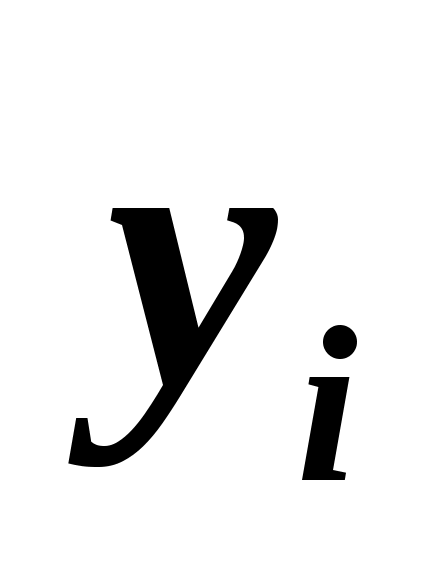
0,03
0,03
0,02
0,04
0,05
0,04